first order system analysis 自控原理一阶系统的matlab分析

最新推荐文章于 2024-01-21 15:53:03 发布

JasonLeaster

最新推荐文章于 2024-01-21 15:53:03 发布

阅读量5.7k

点赞数 4

分类专栏： Adaptive Control 文章标签： matlab 自动控制原理一阶系统

本文链接：https://blog.csdn.net/cinmyheart/article/details/21445731

版权

Adaptive Control 专栏收录该内容

23 篇文章

订阅专栏

本文通过MATLAB仿真研究了一阶系统对阶跃激励的响应，探讨了不同时间常数T下系统响应速度的变化。通过代码实现，直观展示了系统稳定性与响应速度之间的联系。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一阶系统的matlab分析

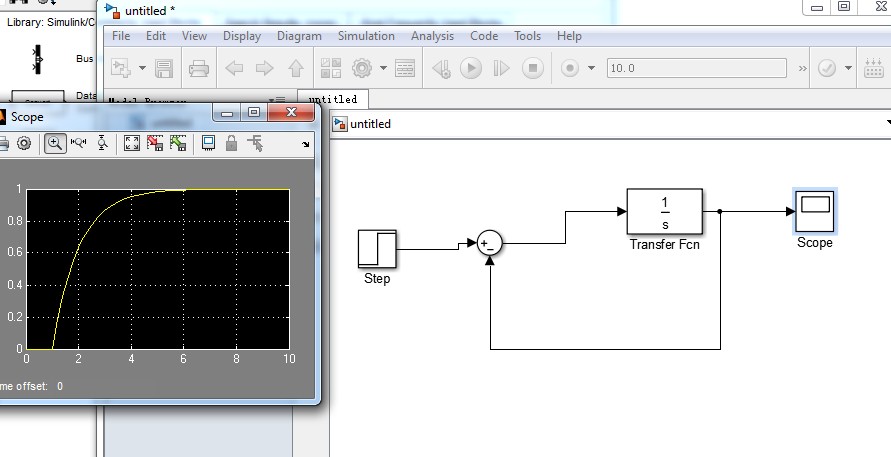
上图是用simulink仿真的一阶系统对阶跃型号的响应

传递函数可以简化为theta(s) = K/(Ts+1)

为方便研究，K为常数，令K等于1。

探究不同的T情况下，一阶系统对阶跃激励的响应。

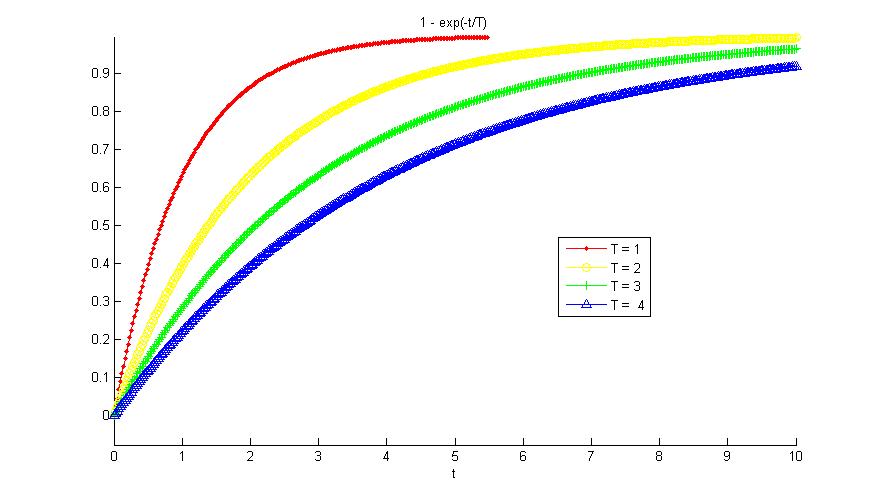
时间常数T越大，反应越迟钝，时间常数T越小，反应越敏捷

代码很简单的，matlab各种封装好的数学处理函数，用起来很方便，和C比起来难度不知道低多少，我们要做的就是不知道就google。然后just use the function is OK！

source code：

%%*************************************************************
% code writer: EOF
% code date:2014.03.18
% e-mail: jasonleaster@gmail.com
% code purpose : 
%           I just want to share with someone who is interesting
% in adaptive control. This code is to help people to understand
% first order system.
%%**************************************************************
clear all
clc
syms s f t m;
K = 1;
hold on;
figure(1);
for  T = 1:4
    f = (K./(T.*s+1)).*(1./s);
    m = ilaplace(f);
    ezplot(m,[0,10]);
end

随着T的增大，可以看出，系统趋向于稳定的时间越长，响应速度越差。

Thank you。