mips指令系统简介

CyberMuse

已于 2024-09-29 21:18:33 修改

阅读量685

点赞数 8

文章标签：系统架构

于 2024-09-29 16:31:48 首次发布

本文链接：https://blog.csdn.net/cocofu/article/details/142638404

版权

**MIPS（Microprocessor without Interlocked Piped Stages）**：这是一种RISC（精简指令集计算）芯片架构，由John L. Hennessy设计，特点是没有内部互锁的流水级，简化了处理器设计。

对比：

RISC（Reduced Instruction Set Computer）架构的核心理念是通过减少和简化处理器的指令集，来提高执行效率和性能。与CISC（复杂指令集计算）不同，RISC采用固定长度的指令和较少的指令类型。

1. **基本概念**：

- **简化指令集**：RISC处理器的指令集较少，每条指令执行时间较短。

- **固定长度指令**：所有指令长度相同，简化了指令解码过程。

- **大量通用寄存器**：RISC处理器通常拥有更多的通用寄存器，减少了对内存的访问次数。

2. **优势**：

- **高效执行**：由于指令集简化，每条指令的执行时间缩短，提高了处理器的执行效率。

- **优化编译**：编译器可以更容易地优化代码，进一步提升性能。

- **低功耗**：简化的设计减少了功耗，适合嵌入式系统等要求低功耗的应用。

CISC（Complex Instruction Set Computer）架构的核心理念是通过提供多种复杂指令，使得每条指令可以执行多步操作，从而简化编程并提高代码密度。

1. **基本概念**：

- **复杂指令集**：CISC处理器的指令集非常丰富，每条指令可以执行多步操作。

- **变长指令**：指令长度不固定，可以根据需要包含多个操作数和操作步骤。

- **内存操作**：CISC处理器可以直接对内存进行复杂操作，减少了指令数目。

2. **特点**：

- **编程简化**：由于指令集丰富，编程时可以使用高层次的指令，减少了程序的复杂度。

- **高代码密度**：复杂指令可以执行多步操作，从而减少了指令数量，提高了代码密度。

- **灵活性高**：CISC架构可以处理多种不同类型的操作和数据结构，灵活性较高。

MIPS架构的核心理念是通过简化指令集和高效的流水线设计来提高处理器的性能和效率。

1. **基本概念**：

- **简化指令集**：MIPS指令集较少且简单，每条指令执行时间固定。

- **流水线设计**：MIPS处理器采用五级流水线（取指、译码、执行、访存、写回），使得多个指令可以并行处理。

- **寄存器丰富**：MIPS拥有32个通用寄存器，减少了对内存的访问。

2. **特点**：

- **高效执行**：指令集简化和流水线设计提高了执行效率。

- **易于编译优化**：编译器可以更容易地优化MIPS代码。

- **模块化设计**：MIPS架构设计简单，易于扩展和实现。

想象一下，我们在一个流水线工厂里，MIPS架构就像这条流水线。每个工人只负责一个简单的步骤（RISC的特点），这样可以提高整体效率。没有互锁的流水级意味着每个工人可以独立工作，不需要等待其他工人的进度。

**小明**：所以，这样的设计让工厂更高效，但需要更多的工人来完成不同的任务（更多的指令）。😮

**王教授**：对，这正是MIPS架构的优势。通过简化每个任务，整体效率反而提高了。因为没有互锁机制，流水线可以更顺畅地运行，减少了等待时间和资源冲突。

再举一个类比，MIPS架构就像学校里的课程安排。每个老师只负责教一门课（简单指令集），这样学生可以在不同的时间段学习不同的科目，而不需要等上一门课结束才能开始下一门课。这样安排的好处是，学生的学习效率更高，也减少了时间浪费。

最后一个例子，想象你在组装家具，MIPS架构就像你有一张详细的说明书（简单指令集），每一步都很明确，不会出错。这种设计简化了每一步操作，虽然每一步都很简单，但整体效率提升了。

**小明**：所以，MIPS架构通过简化每一步操作（RISC），提高了整体效率。😅

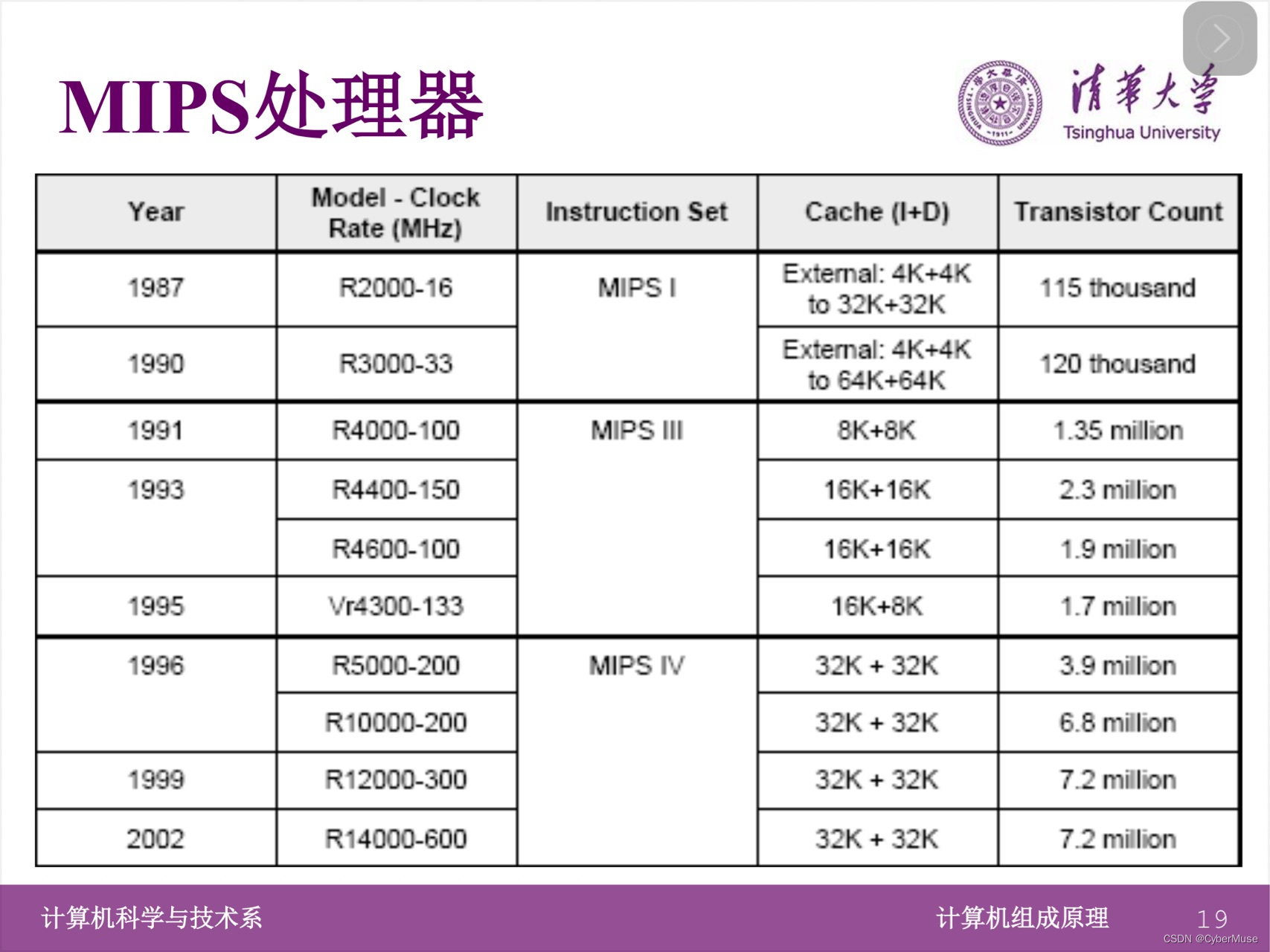
### MIPS处理器发展历程总结

#### 清华大学计算机科学与技术系
#### 计算机组成原理

以下是MIPS处理器从1987年至2002年的发展历程总结，包括各型号的时钟频率、指令集、缓存配置和晶体管数量。

| 年份 | 型号 | 时钟频率(MHz) | 指令集 | 缓存(I+D) | 晶体管数量 |
| ----- | -------------- | ------------- | --------- | ------------- | --------------- |
| 1987 | R2000-16 | 16 | MIPS I | 外部: 4K+4K 至 32K+32K | 115 千 |
| 1990 | R3000-33 | 33 | MIPS I | 外部: 4K+4K 至 64K+64K | 120 千 |
| 1991 | R4000-100 | 100 | MIPS III | 8K+8K | 1.35 百万 |
| 1993 | R4400-150 | 150 | MIPS III | 16K+16K | 2.3 百万 |
| | R4600-100 | 100 | MIPS III | 16K+16K | 1.9 百万 |
| 1995 | Vr4300-133 | 133 | MIPS III | 16K+8K | 1.7 百万 |
| 1996 | R5000-200 | 200 | MIPS IV | 32K+32K | 3.9 百万 |
| | R10000-200 | 200 | MIPS IV | 32K+32K | 6.8 百万 |
| 1999 | R12000-300 | 300 | MIPS IV | 32K+32K | 7.2 百万 |
| 2002 | R14000-600 | 600 | MIPS IV | 32K+32K | 7.2 百万 |

### 关键点总结

1. **指令集演进**：
- 1987年的R2000和1990年的R3000处理器采用MIPS I指令集。
- 1991年的R4000处理器引入了MIPS III指令集。
- 1996年的R5000开始采用更先进的MIPS IV指令集。

2. **时钟频率提升**：
- 处理器时钟频率从1987年R2000的16 MHz逐渐提升到2002年R14000的600 MHz，显示了显著的性能提升。

3. **缓存配置**：
- 早期处理器（如R2000和R3000）采用外部缓存，容量从4K+4K到64K+64K不等。
- 随着技术进步，处理器集成的缓存容量显著增加，如R4000的8K+8K和R14000的32K+32K。

4. **晶体管数量增加**：
- 晶体管数量从1987年R2000的115千增加到2002年R14000的7.2百万，显示了处理器复杂性的显著提高。

通过这些数据，可以看出MIPS处理器在指令集、时钟频率、缓存配置和晶体管数量等方面的持续进步，推动了计算性能的不断提升。

- **rs**: **Source Register**
- **rt**: **Target Register**
- **rd**: **Destination Register**

MIPS寄存器型指令格式用于寄存器之间的操作。以下是对各字段的详细解释，并在每个类别下举例说明。

#### 寄存器型指令格式表格

| 字段 | 位数 | 说明 | 英文缩写原词 |
| ----- | ----- | ------------- | ------------ |
| op | 6位 | 操作码 | Opcode |
| rs | 5位 | 源寄存器1 | Source Register 1 |
| rt | 5位 | 源寄存器2 | Source Register 2 |
| rd | 5位 | 目标寄存器 | Destination Register |
| shamt | 5位 | 移位量（用于移位指令） | Shift Amount |
| funct | 6位 | 功能码 | Function Code |

#### 逐项解释及举例

1. **操作码（op）**

- **位数**：6位

- **说明**：操作码决定了指令的类型。例如，操作码可能指示这是一个加法操作、减法操作或是其他类型的运算。

- **类比**：操作码就像是指令的“动词”，决定了指令的基本操作类型。

- **举例**：

- `add $1, $2, $3`中的操作码为`000000`，表示这是一个算术操作。

- `sub $4, $5, $6`中的操作码也是`000000`，表示也是一个算术操作，但具体操作由功能码决定。

2. **源寄存器1（rs）**

- **位数**：5位

- **说明**：源寄存器1是第一个操作数的寄存器。它提供了参与运算的一个数据。

- **类比**：可以将其类比为加法运算中的第一个加数。

- **举例**：

- `add $1, $2, $3`中，`$2`是源寄存器1，提供了第一个操作数。

- `sub $4, $5, $6`中，`$5`是源寄存器1，提供了第一个操作数。

3. **源寄存器2（rt）**

- **位数**：5位

- **说明**：源寄存器2是第二个操作数的寄存器。它提供了参与运算的另一个数据。

- **类比**：可以将其类比为加法运算中的第二个加数。

- **举例**：

- `add $1, $2, $3`中，`$3`是源寄存器2，提供了第二个操作数。

- `sub $4, $5, $6`中，`$6`是源寄存器2，提供了第二个操作数。

4. **目标寄存器（rd）**

- **位数**：5位

- **说明**：目标寄存器是用于存储运算结果的寄存器。例如，加法操作的结果会被存储在目标寄存器中。

- **类比**：可以将其类比为加法运算的结果存储位置。

- **举例**：

- `add $1, $2, $3`中，`$1`是目标寄存器，存储运算结果。

- `sub $4, $5, $6`中，`$4`是目标寄存器，存储运算结果。

5. **移位量（shamt）**

- **位数**：5位

- **说明**：移位量用于移位指令中，表示需要移位的位数。对于非移位指令，这个字段通常为0。

- **类比**：就像我们在做二进制位移操作时，决定向左或向右移动的位数。

- **举例**：

- `sll $1, $2, 4`中，移位量为`4`，表示将寄存器`$2`的值左移4位。

- `srl $3, $4, 2`中，移位量为`2`，表示将寄存器`$4`的值右移2位。

6. **功能码（funct）**

- **位数**：6位

- **说明**：功能码进一步指定了操作类型，特别是对于相同操作码的不同变种。例如，操作码可能指示这是一个算术操作，而功能码决定是加法还是减法。

- **类比**：功能码就像是指令的“副词”，细化了操作的具体类型。

- **举例**：

- `add $1, $2, $3`中，功能码为`100000`，表示这是一个加法操作。

- `sub $4, $5, $6`中，功能码为`100010`，表示这是一个减法操作。

#### 总结

MIPS寄存器型指令格式通过操作码和功能码的组合，实现了灵活且高效的指令集设计。不同字段的明确分工，使得每条指令都能够被快速解码和执行。这种设计不仅简化了硬件电路的复杂性，也提高了指令执行的速度和效率。

希望通过以上解析和举例，你能更直观地理解MIPS寄存器型指令格式的设计理念和实际应用。如果有任何疑问，欢迎随时提问！

【注】

`sll` 和 `srl` 是 MIPS 指令集中的两条移位指令，它们的原词如下：

- **sll**: **Shift Left Logical**
- **srl**: **Shift Right Logical**

这两条指令用于对寄存器中的数据进行逻辑移位操作：

- `sll` 指令将寄存器中的值向左移位，并在右边填充0。
- `srl` 指令将寄存器中的值向右移位，并在左边填充0。

在计算机科学中，“逻辑移位”（logical shift）和“算术移位”（arithmetic shift）是两种不同的移位操作。之所以加上“logical”这个词，是为了区分这两种操作。

### 逻辑移位（Logical Shift）

- **逻辑左移（Shift Left Logical, SLL）**：将二进制数向左移位，右边填充0。左移时，最左边的位被移出并丢弃，右边新填充的位为0。
- **逻辑右移（Shift Right Logical, SRL）**：将二进制数向右移位，左边填充0。右移时，最右边的位被移出并丢弃，左边新填充的位为0。

### 算术移位（Arithmetic Shift）

- **算术左移**：与逻辑左移相同，即向左移位，右边填充0。
- **算术右移（Shift Right Arithmetic, SRA）**：将二进制数向右移位，但左边填充的是原来最高位的值（即符号位），保持符号不变。这个操作主要用于带符号整数的右移，可以保持数值的符号。

### 举例说明

假设一个8位的二进制数 `1011 0010`：

- **逻辑左移2位（SLL 2）**：`1011 0010` 变为 `1100 1000`（右边填充两个0）
- **逻辑右移2位（SRL 2）**：`1011 0010` 变为 `0010 1100`（左边填充两个0）
- **算术右移2位（SRA 2）**：`1011 0010` 变为 `1110 1100`（左边填充两个符号位，即原最高位1）

### 结论

加上“logical”这个词，是为了明确表示移位过程中填充的是0，而不是根据符号位填充。这在无符号数处理或需要进行逻辑操作时尤为重要。

符号位（Sign Bit）是用于表示一个二进制数符号（正或负）的特定位。通常在计算机中，符号位是最高位（最左边的位）。在带符号数表示法中，符号位的值决定了数的符号：

- **0** 表示正数
- **1** 表示负数

### 常见的符号数表示法

1. **原码（Sign and Magnitude）**:
- 最高位是符号位，其余位表示数值的大小。
- 例如，8位表示法中，`+5` 表示为 `0000 0101`，`-5` 表示为 `1000 0101`。

2. **反码（One's Complement）**:
- 最高位是符号位，正数的表示与原码相同，负数的表示是对数值位取反（即 0 变 1，1 变 0）。
- 例如，8位表示法中，`+5` 表示为 `0000 0101`，`-5` 表示为 `1111 1010`。

3. **补码（Two's Complement）**:
- 最高位是符号位，正数的表示与原码相同，负数的表示是对数值位取反后加1。
- 例如，8位表示法中，`+5` 表示为 `0000 0101`，`-5` 表示为 `1111 1011`。

### 为什么使用补码？

补码在计算机中广泛使用，因为它有许多优点：

1. **简化算术运算**：
- 不需要单独的减法电路，减法可以用加法实现。
- 例如，`5 - 3` 可以表示为 `5 + (-3)`。

2. **唯一的零表示**：
- 反码和原码都有两个零（正零和负零），而补码只有一个零表示（`0000 0000`）。

3. **符号扩展简单**：
- 在进行位扩展时，只需重复符号位即可，不需要额外处理。

### 符号位在移位操作中的作用

- **逻辑移位（Logical Shift）**：符号位不参与填充，移位后填充0。
- 例如，`1011 0010` 向右逻辑移位2位：`0010 1100`。

- **算术移位（Arithmetic Shift）**：符号位保持不变，移位后填充符号位的值。
- 例如，`1011 0010` 向右算术移位2位：`1110 1100`。

符号位在保持带符号数运算和表示时起到了关键作用，确保了数值的正确性和计算的简便性。如果有更多问题，欢迎继续提问！

【注】

当然，以下是对补码优点的具体举例说明：

### 1. 简化算术运算

在补码表示法中，减法可以转换为加法，简化了硬件电路设计。

**例如：**

计算 `5 - 3`：

- 十进制表示：`5 - 3 = 2`
- 二进制表示（假设使用8位）：
- `5` 的补码表示：`0000 0101`
- `3` 的补码表示：`0000 0011`
- `-3` 的补码表示：取反加1，即 `1111 1101`

现在计算 `5 + (-3)`：

```
0000 0101
+ 1111 1101
------------
0000 0010 (结果为2)
```

通过将减法转换为加法，简化了电路设计。

### 2. 唯一的零表示

补码表示法中，零只有一种表示方法，而反码和原码中则有两个表示。

**例如：**

- 原码表示中：
- `+0`：`0000 0000`
- `-0`：`1000 0000`

- 反码表示中：
- `+0`：`0000 0000`
- `-0`：`1111 1111`

- 补码表示中：
- `+0` 和 `-0` 都表示为：`0000 0000`

这种唯一的零表示简化了零值的处理和比较。

### 3. 符号扩展简单

在进行位扩展时，补码表示法只需重复符号位即可，不需要额外处理。

**例如：**

假设我们有一个8位的带符号二进制数 `-3`，其补码表示为 `1111 1101`。现在我们需要将它扩展为16位：

- 原来的8位数： `1111 1101`
- 扩展为16位： `1111 1111 1111 1101`

符号位（最左边的位）在扩展过程中被简单地复制，从而保持了数值的正确性。

这些优点使得补码在计算机系统中得到了广泛应用。如果有其他问题，欢迎继续提问！

好的，下面我将以直觉型、视觉型学习风格，采用教科书式、通俗易懂的方式，详细解释补码表示法的原理，并一步步推导其机理。

### 补码表示法的优点

1. **简化算术运算**
2. **唯一的零表示**
3. **符号扩展简单**

### 1. 简化算术运算

#### 理论机制

补码表示法使得减法可以通过加法实现。负数的补码表示是其正数的反码加1，这样减法运算就变成了加法运算，简化了硬件电路设计。

#### 数学推导与证明

- **步骤1**：定义正数和负数的补码表示

对于一个8位二进制数 $ A $ 和 $ B $，假设 $ A = 5 $ 和 $ B = 3 $。

- $ A = 5 $ 的二进制（原码）表示：
\[
0000 0101
\]

- $ B = 3 $ 的二进制（原码）表示：
\[
0000 0011
\]

- **步骤2**：计算 $ -B $ 的补码表示

$ -B $ 的补码表示是 $ B $ 的反码加1。

- $ B = 3 $ 的反码：
\[
0000 0011 \quad \text{取反} \quad 1111 1100
\]

- 加1得到补码：
\[
1111 1100 + 1 = 1111 1101
\]

- **步骤3**：将减法转换为加法，并进行运算

$ A - B $ 转换为 $ A + (-B) $：

- $ A = 5 $ 的补码表示：
\[
0000 0101
\]

- $ -B = -3 $ 的补码表示：
\[
1111 1101
\]

- 进行二进制加法运算：
\[
0000 0105 \quad \text{(5)}
\]
\[
+ 1111 1101 \quad \text{(-3)}
\]
\[
------------
\]
\[
0000 0010 \quad \text{(结果为2，正确结果)}
\]

通过上述步骤，我们可以看到补码表示法将减法转换为加法，简化了电路设计。

### 2. 唯一的零表示

#### 理论机制

在补码表示法中，零只有一种表示方法，而在原码和反码表示中，零可能有两个表示。这种唯一性简化了对零值的处理和比较。

#### 数学推导与证明

- **原码表示**：
\[
+0: \quad 0000 0000
\]
\[
-0: \quad 1000 0000
\]

- **反码表示**：
\[
+0: \quad 0000 0000
\]
\[
-0: \quad 1111 1111
\]

- **补码表示**：
\[
0: \quad 0000 0000
\]

在补码表示法中，零始终表示为 `0000 0000`，这简化了对零值的处理和比较。

### 3. 符号扩展简单

#### 理论机制

在进行位扩展时，补码表示法只需重复符号位即可，不需要额外处理。符号位（最高位）决定了数值的正负性，扩展时保持符号位即可保证数值的正确性。

#### 数学推导与证明

假设我们有一个8位的带符号二进制数 `-3`，其补码表示为 `1111 1101`。现在我们需要将它扩展为16位：

- **原来的8位数**：
\[
1111 1101
\]

- **扩展为16位**：
\[
1111 1111 1111 1101
\]

符号位（最左边的位）在扩展过程中被简单地复制，从而保持了数值的正确性。这是因为在补码表示法中，符号位决定了数值的正负性，重复符号位可以确保扩展后的数值与原数值保持一致。

### 表格信息总结

| 优点 | 理论机制 | 数学推导与证明 |
|---------------------|----------------------------------|-----------------------------------------------------------------------|
| 简化算术运算 | 减法转换为加法 | `5 - 3` 转换为 `5 + (-3)`，通过补码加法得到正确结果 `0000 0010` |
| 唯一的零表示 | 只有一种零表示 | 补码中零表示为 `0000 0000` |
| 符号扩展简单 | 只需重复符号位 | `1111 1101` 扩展为 `1111 1111 1111 1101` |

通过以上推导和证明，我们可以清晰地看到补码表示法在计算机系统中的优势和理论基础。如果有其他问题，欢迎继续提问！

好的，作为一名有20年教学和研究经验的理论数学和离散数学、数论方向的硕士生导师，我将从理论数学和离散数学、数论的角度，详细解释和证明补码表示法的合理性。

### 理论背景

在计算机科学中，补码表示法是一种用于表示有符号整数的方法。这种表示法利用模运算的性质，使得二进制加法和减法在硬件电路中得以简化。

### 1. 模运算与补码表示法

#### 理论基础

在数学中，模运算（模算术）是一个重要的概念，尤其是在数论中。对于一个整数 $ x $，模 $ 2^n $ 的运算定义为：
\[ x \mod 2^n \]

对于一个 $ n $ 位二进制数，其取值范围是 $ 0 $ 到 $ 2^n - 1 $。在补码表示法中，我们利用模 $ 2^n $ 的性质来表示负数。

#### 数学推导与证明

- **步骤1**：定义补码

对于一个 $ n $ 位的整数 $ x $，其补码表示定义为：
\[
x_{\text{补码}} = \begin{cases}
x & \text{if } 0 \le x < 2^{n-1} \\
x - 2^n & \text{if } 2^{n-1} \le x < 2^n
\end{cases}
\]

- **步骤2**：负数的补码表示

设 $ x $ 是一个 $ n $ 位二进制数，且 $ x $ 的补码表示为 $ -x $。根据补码的定义：
\[
-x_{\text{补码}} = 2^n - x
\]

- **步骤3**：验证补码的加法运算

假设我们有两个 $ n $ 位整数 $ A $ 和 $ B $，且 $ A $ 的补码表示为 $ A_{\text{补码}} $，$ B $ 的补码表示为 $ B_{\text{补码}} $。我们需要证明：
\[
A_{\text{补码}} + B_{\text{补码}} \equiv (A + B) \mod 2^n
\]

通过模运算的性质：
\[
(A_{\text{补码}} + B_{\text{补码}}) \mod 2^n = ((A \mod 2^n) + (B \mod 2^n)) \mod 2^n = (A + B) \mod 2^n
\]

这证明了补码表示法在加法运算中的正确性。对于减法 $ A - B $，可以看作 $ A + (-B) $，其中 $ -B $ 的补码表示为 $ 2^n - B $。

### 2. 唯一的零表示

#### 理论基础

在补码表示法中，零的唯一表示是由模运算的性质决定的。模 $ 2^n $ 的运算结果总是落在 $ 0 $ 到 $ 2^n - 1 $ 之间，这保证了零只有一种表示。

#### 数学推导与证明

- **步骤1**：定义零的补码表示

对于一个 $ n $ 位的整数零 $ 0 $，其补码表示为：
\[
0_{\text{补码}} = 0
\]

不存在其他表示，因为模 $ 2^n $ 运算中，只有 $ 0 \mod 2^n = 0 $。

### 3. 符号扩展简单

#### 理论基础

在补码表示法中，符号位（最高位）用于表示数值的正负性。符号位决定了补码数值在进行位扩展时的正确性。

#### 数学推导与证明

- **步骤1**：定义符号扩展

假设我们有一个 $ n $ 位的补码数 $ x $，其符号位为 $ x_{n-1} $。当我们将其扩展为 $ m $ 位（$ m > n $）时，符号扩展的规则是保持符号位不变。

- **步骤2**：验证符号扩展的正确性

对于一个 $ n $ 位的补码数 $ x $，其扩展后的 $ m $ 位表示为：
\[
x_{\text{扩展}} = \begin{cases}
0^{m-n} x & \text{if } x_{n-1} = 0 \\
1^{m-n} x & \text{if } x_{n-1} = 1
\end{cases}
\]

由此，扩展后的数值保持了原数值的正确性，因为符号位的扩展确保了数值的符号和大小不变。

### 总结

通过以上数论和离散数学的推导和证明，我们可以清晰地看到补码表示法在计算机系统中的合理性和数学基础。如果有其他问题，欢迎继续提问！

好的，作为一名有20年教学和研究经验的ISTJ硕士生导师，我将整理和总结以上内容，并结合立即数型指令格式（I型）的解释，进行详细说明。

### 补码表示法的优点总结与解释

1. **简化算术运算**
- **理论机制**：补码表示法使得减法可以通过加法实现，简化了硬件电路设计。
- **数学推导**：对于一个整数 $ x $，其补码表示为 $ -x $，实际计算中表现为 $ 2^n - x $。
- **示例**：假设 $ A = 5 $ 和 $ B = 3 $，其补码表示分别为 $ 0000 0101 $ 和 $ 1111 1101 $。计算 $ A - B $ 实际上是 $ 0000 0101 + 1111 1101 = 0000 0010 $（结果为2）。

2. **唯一的零表示**
- **理论机制**：补码表示法中，零只有一种表示方法，避免了原码和反码中的双零表示问题。
- **数学推导**：在补码表示法中，零始终表示为 $ 0000 0000 $。
- **示例**：对于一个8位二进制数，零的补码表示为 $ 0000 0000 $，不存在其他表示。

3. **符号扩展简单**
- **理论机制**：补码表示法中，符号位（最高位）用于表示数值的正负性，扩展时保持符号位即可。
- **数学推导**：对于一个8位的带符号二进制数 $ -3 $，其补码表示为 $ 1111 1101 $。扩展为16位时，符号位保持不变，表示为 $ 1111 1111 1111 1101 $。
- **示例**：将8位数 $ 1111 1101 $ 扩展为16位，结果为 $ 1111 1111 1111 1101 $，符号位保持一致，数值正确。

### 立即数型指令格式（I型）

立即数型指令用于包含立即数的操作，指令格式如下：

| 字段 | 位数 | 说明 |
| ------------------- | ----- | ------------- |
| op | 6位 | 操作码 |
| rs | 5位 | 源寄存器 |
| rt | 5位 | 目标寄存器 |
| address/immediate | 16位 | 地址或立即数 |

#### 示例1：`lw $1, 100($2)`

- **功能**：从内存中加载数据到寄存器$1，地址由寄存器$2的值加上偏移量100决定。
- **表示**：`R1 <- M[R2 + 100]`

**解释**：
- **op**：加载字指令的操作码（假设为`100011`）。
- **rs**：源寄存器$2（假设寄存器编号为`00010`）。
- **rt**：目标寄存器$1（假设寄存器编号为`00001`）。
- **address/immediate**：偏移量100（16位二进制表示为`0000 0000 0110 0100`）。

**指令具体表示**：
```
100011 00010 00001 0000 0000 0110 0100
```

#### 示例2：`addi $1, $2, 100`

- **功能**：将寄存器$2的值与立即数100相加，结果存入寄存器$1。
- **表示**：`R1 <- R2 + 100`

**解释**：
- **op**：加立即数指令的操作码（假设为`001000`）。
- **rs**：源寄存器$2（假设寄存器编号为`00010`）。
- **rt**：目标寄存器$1（假设寄存器编号为`00001`）。
- **address/immediate**：立即数100（16位二进制表示为`0000 0000 0110 0100`）。

**指令具体表示**：
```
001000 00010 00001 0000 0000 0110 0100
```

### 总结

通过以上内容，我们深刻理解了补码表示法的优点及其数学基础，同时掌握了立即数型指令格式（I型）的构成和具体示例。每个示例通过直观的二进制表示，使得复杂的概念变得通俗易懂。希望这些内容能帮助你更好地理解相关知识。如果有任何疑问，欢迎继续提问！

【注】

`lw` 是计算机体系结构中的一条指令，具体解释如下：

### `lw` 指令解释

#### 定义和功能
- **全称**：`lw` 代表 "Load Word"（加载字）。
- **功能**：从内存中加载一个字（通常为4字节）到指定的寄存器。

#### 指令格式
`lw $rt, offset($rs)`

- **$rt**：目标寄存器，数据将被加载到该寄存器中。
- **offset**：偏移量（立即数），用于计算内存地址。
- **$rs**：源寄存器，包含基地址。

#### 操作过程
1. **计算内存地址**：将源寄存器 $rs 的值与偏移量相加，得到内存地址。
2. **加载数据**：从计算出的内存地址中读取一个字的数据。
3. **存储数据**：将读取的数据存储到目标寄存器 $rt 中。

#### 示例和具体说明

**示例**：`lw $1, 100($2)`
- **功能**：从内存中加载数据到寄存器 $1，地址由寄存器 $2 的值加上偏移量 100 决定。
- **表示**：`R1 <- M[R2 + 100]`

**解释**：
- **`$1`**：目标寄存器，存放加载的数据。
- **`100($2)`**：内存地址，由寄存器 $2 的值加上偏移量 100 计算得出。

**指令具体表示**：
```
op: 100011
rs: 00010 (寄存器 $2)
rt: 00001 (寄存器 $1)
address/immediate: 0000 0000 0110 0100
```
**二进制表示**：
```
100011 00010 00001 0000 0000 0110 0100
```

### 总结
`lw` 指令用于从内存中加载一个字（4字节）到指定寄存器中，通过源寄存器的值和偏移量计算内存地址。希望这个解释能帮助你更好地理解 `lw` 指令的功能和使用。如果有进一步的问题，欢迎继续提问！

好的，作为一名有20年教学和研究经验的ISTJ硕士生导师，我将介绍伪代码 `R1 <- M[R2 + 100]`，并分点解释说明，同时在每个类别下举例说明。

### 伪代码介绍

`R1 <- M[R2 + 100]` 是一种伪代码（pseudo-code）表示形式，用于描述计算机指令的操作。该表达式表示将内存地址 `R2 + 100` 处的值加载到寄存器 `R1` 中。这种表示方法简洁明了，便于理解和传达指令的基本操作。

### 详细解释

1. **R1**
- **说明**：目标寄存器（Target Register），用于存放从内存中加载的数据。
- **类比**：可以将其类比为一个存储柜，用于存放操作结果。

2. **M[R2 + 100]**
- **说明**：内存地址（Memory Address），由寄存器 `R2` 的值加上立即数 `100` 计算得到。
- **类比**：可以将其类比为一个存放在指定位置的文件，该位置由基础位置（R2）和偏移量（100）决定。

3. **<-**
- **说明**：赋值操作符（Assignment Operator），表示将右侧的值赋给左侧。
- **类比**：可以将其类比为将文件内容复制到存储柜中的操作。

### 示例说明

#### 示例1：加载字指令（Load Word Instruction）

**伪代码**：`lw $1, 100($2)`
- **功能**：从内存中加载数据到寄存器 `$1`，地址由寄存器 `$2` 的值加上偏移量 `100` 决定。
- **表示**：`R1 <- M[R2 + 100]`
- **解释**：
- **`lw`**：代表 "Load Word"，从内存加载一个字（4字节）到寄存器。
- **`$1`**：目标寄存器，存放加载的数据。
- **`100($2)`**：内存地址，由寄存器 `$2` 的值加上偏移量 `100` 计算得出。

#### 示例2：立即数加法指令（Add Immediate Instruction）

**伪代码**：`addi $1, $2, 100`
- **功能**：将寄存器 `$2` 的值与立即数 `100` 相加，结果存入寄存器 `$1`。
- **表示**：`R1 <- R2 + 100`
- **解释**：
- **`addi`**：代表 "Add Immediate"，进行立即数加法。
- **`$1`**：目标寄存器，存放加法结果。
- **`$2`**：源寄存器，提供操作数。
- **`100`**：立即数，与源寄存器的值相加。

### 类比与归纳

1. **类比**：
- 将寄存器类比为存储柜，内存地址类比为文件位置，赋值操作类比为文件内容复制。
- 例如，`R1 <- M[R2 + 100]` 就像是将文件 `R2 + 100` 处的内容复制到存储柜 `R1` 中。

2. **归纳**：
- 通过这两个示例，我们归纳出伪代码的表示方法和计算机指令的基本操作逻辑。
- `R1 <- M[R2 + 100]` 代表从内存地址 `R2 + 100` 处加载数据到寄存器 `R1`。
- `R1 <- R2 + 100` 代表将寄存器 `R2` 的值与立即数 `100` 相加，结果存入寄存器 `R1`。

### 总结

伪代码 `R1 <- M[R2 + 100]` 通过简单的符号和操作符，清晰地描述了将内存数据加载到寄存器中的操作。通过具体的指令示例，如 `lw` 和 `addi`，我们可以更好地理解这种伪代码的实际应用。希望这些解释能帮助你深入理解相关知识。如果有任何疑问，欢迎继续提问！

不，以上两个示例的操作结果是不一样的。尽管它们看起来相似，但它们执行的操作本质上是不同的。让我们详细解释一下这两个示例的区别。

### 示例1：加载字指令（Load Word Instruction）

**操作结果**：
- 假设 `R2` 的值为 `2000`，则 `M[R2 + 100]` 指的是内存地址 `2100` 处的内容。
- 如果内存地址 `2100` 处的值是 `5000`，那么 `R1` 将被赋值 `5000`。

### 示例2：立即数加法指令（Add Immediate Instruction）

**操作结果**：
- 假设 `R2` 的值为 `2000`，则 `R2 + 100` 等于 `2100`。
- 因此，`R1` 将被赋值 `2100`。

### 总结

尽管这两个示例都涉及到寄存器和立即数 `100`，它们的操作是不同的：

- **示例1**：`lw $1, 100($2)` 从内存地址 `R2 + 100` 处加载数据到寄存器 `$1`。
- **示例2**：`addi $1, $2, 100` 将寄存器 `$2` 的值与立即数 `100` 相加，并将结果存入寄存器 `$1`。

因此，操作结果取决于内存地址 `R2 + 100` 处的内容和寄存器 `R2` 的值。在大多数情况下，这两个指令的结果不相同。

#### 3. 转移型指令格式（J型）

转移型指令用于跳转操作，指令格式如下：

| 字段 | 位数 | 说明 |

| ------- | ----- | -------- |

| op | 6位 | 操作码 |

| address | 26位 | 目标地址 |

**示例**：`j 8000`

- 功能：跳转到地址`PC[31:28] | (8000 << 2)`。

- 表示：`PC <- (PC[31:28] << 28) | (8000 << 2)`

### 操作数寻址方式

MIPS指令集支持三种操作数寻址方式：

1. **基址加16位位移量的访存寻址**：

- 例如：`lw $1, 100($2)`

- 说明：从内存中加载数据，地址由寄存器$2的值加上偏移量100决定。

2. **立即数寻址**：

- 例如：`addi $1, $2, 100`

- 说明：将寄存器$2的值与立即数100相加，结果存入寄存器$1。

3. **寄存器寻址**：

- 例如：`add $1, $2, $3`

- 说明：将两个源寄存器$2和$3的值相加，结果存入目标寄存器$1。

通过以上总结，我们可以清楚地了解MIPS指令格式及其操作数寻址方式，便于进一步深入学习和应用。

好的，下面是一个更具体的示例，说明 `PC[31:28] | (8000 × 4)` 的计算过程，并包含所需的先修知识。

### 示例说明

假设当前 `PC` 值为 `0x00400000`，并且要处理的指令是 `j 0x8000`。

#### 先修知识

1. **程序计数器（PC）**：
- `PC` 是程序计数器，指向当前正在执行的指令的地址。

2. **指令格式**：
- MIPS指令 `j target_address`，其中 `target_address` 是指令要跳转到的目标地址。

3. **二进制和十六进制**：
- 进制转换：`0x8000` 转换为二进制是 `1000 0000 0000 0000`。
- 位操作：左移和按位或操作。

4. **MIPS架构**：
- MIPS指令集和跳转指令的格式。

#### 计算步骤

1. **取 `PC[31:28]`**：
- 当前 `PC` 值为 `0x00400000`，二进制表示为 `0000 0100 0000 0000 0000 0000 0000 0000`。
- `PC[31:28]` 为高4位，即 `0000`。十六进制表示为 `0x0`。

2. **转换并计算目标地址**：
- 目标地址 `0x8000`：
- 十六进制 `0x8000` 转换为二进制为 `1000 0000 0000 0000`。
- 目标地址左移2位（乘以4）：
- 二进制 `1000 0000 0000 0000` 左移2位后为 `1000 0000 0000 0000 00`，即 `0x20000`。

3. **组合地址**：
- 将 `PC[31:28]` 与目标地址左移后的结果进行按位或操作：
- `PC[31:28]` 是 `0x0`，二进制为 `0000`。
- 目标地址左移后的结果是 `0x20000`，二进制为 `0000 0010 0000 0000 0000 0000 0000 0000`。
- 按位或操作：`0000 0000 0000 0000 0000 0000 0000 0000` | `0000 0010 0000 0000 0000 0000 0000 0000` 结果为 `0000 0010 0000 0000 0000 0000 0000 0000`。
- 即新的地址为 `0x0020000`。

### 结果

- 通过上述计算，最终跳转到的目标地址为 `0x0020000`。

### 总结

通过这个示例，我们可以看到以下步骤和相关的先修知识：

1. **程序计数器（PC）**：理解 `PC` 的作用。
2. **指令格式**：了解 MIPS 跳转指令格式。
3. **进制转换**：能从十六进制转换到二进制，并理解二进制左移操作。
4. **位操作**：理解按位或操作如何组合地址。
5. **MIPS架构**：理解 MIPS 指令集和跳转指令的地址计算方法。

这些知识点结合起来，使我们能够正确地计算出跳转指令的目标地址。

好的，让我们具体分析从什么地址跳到什么地址。

### 假设
当前程序计数器（PC）的值为 `0x00400000`，指令是 `j 0x8000`。

### 具体步骤

#### 1. 提取目标地址
目标地址字段为 `0x8000`（十六进制），转换为二进制为：
```
1000 0000 0000 0000
```

#### 2. 左移2位（乘以4）
为了得到字节地址，我们需要将目标地址左移2位：
```
1000 0000 0000 0000 << 2 = 1000 0000 0000 0000 00
```
转换为十六进制为 `0x20000`。

#### 3. 组合高4位
在MIPS架构中，跳转指令的目标地址是一个伪指令地址，需要组合当前PC的高4位。
- 当前PC值为 `0x00400000`，二进制表示为：
```
0000 0100 0000 0000 0000 0000 0000 0000
```
- 高4位为 `0000`，十六进制为 `0x0`。

#### 4. 计算最终跳转地址
将高4位与目标地址组合：
```
0x0 << 28 | 0x20000 = 0x0020000
```
即最终跳转地址为 `0x0020000`。

### 总结
- **从地址**：`0x00400000`
- **到地址**：`0x0020000`

因此，执行跳转指令 `j 0x8000` 将使程序从地址 `0x00400000` 跳转到地址 `0x0020000`。

好的，让我们具体分析字对齐对上述操作的影响。

### 假设
当前程序计数器（PC）的值为 `0x00400000`，指令是 `j 0x8000`。

### 具体步骤

#### 1. 提取目标地址

目标地址字段为 `0x8000`（十六进制），转换为二进制为：
```
1000 0000 0000 0000
```

#### 2. 左移2位（乘以4）

为了得到字节地址，我们需要将目标地址左移2位：
```
1000 0000 0000 0000 << 2 = 1000 0000 0000 0000 00
```
转换为十六进制为 `0x20000`。

#### 3. 组合高4位

在MIPS架构中，跳转指令的目标地址是一个伪指令地址，需要组合当前PC的高4位。
- 当前PC值为 `0x00400000`，二进制表示为：
```
0000 0100 0000 0000 0000 0000 0000 0000
```
- 高4位为 `0000`，十六进制为 `0x0`。