Zemax单透镜的优化设计（Single Lens/Singlet）

0.题目

一、单透镜的优化设计（Single Lens/Singlet）

1. 设计参数与要求

（1）入瞳直径为50.00mm；

（2）系统F数为4.0；

（3）全视场角为8度；

（4）工作波长为588nm；

（5）材料为光学玻璃或光学塑料；

（6）学号尾号为双数同学：光阑到第一个光学面的距离范围为2mm-6mm，透镜中心厚度范围为5.00-10.00mm；

（7）学号尾号为单数同学：光阑到第一个光学面的距离范围为6mm-10mm，透镜中心厚度范围为10.00-15.00mm；

（8）设计目标为Spot Diagram的均方根半径在近轴像面小；

（9）光学与结构参数均保留小数点后三位；

（10）无其他限制；（以上仅采用球面光学面进行设计）

（11）进一步，利用单个非球面提升单透镜的性能，并输出结果。

2. 设计结果

（1）2D和3D系统图；

（2）系统参数数据（Prescription Data）及评价（下述内容以表格或图的形式给出）；

* General Lens Data；

* Field；

* Wavelength；

* Surface Data Summary；

* Spot Diagram；

* RMS vs Field Plot

（3）对比分析仅采用球面光学面设计与引入非球面设计前后单透镜光学系统的成像质量变化。

3. 阐述单透镜设计过程中关键参数计算及其优化设计思路（Tips和Tricks）（字数不限）

---

1.设计参数与要求

（1）入瞳直径为50.00mm;

新建的项目

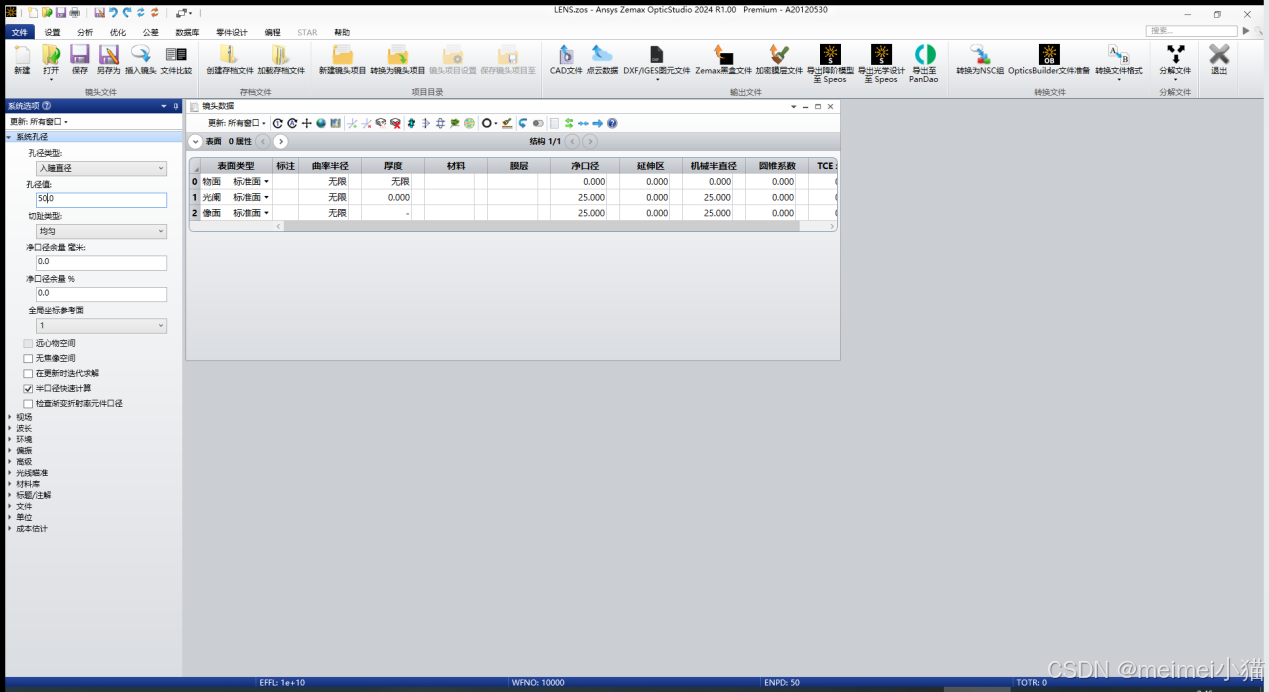
设置入瞳直径为50.0

设置单位为毫米（mm）

（2）系统F数为4.0;

  F数与焦距和入瞳直径有以下关系：

本题的F数为4，入瞳直径为50.00mm，故焦距（EFFL）为200.00mm。

系统F数的设定方法有两种，第一种可以在评价函数中添加EFFL操作数，使之目标为200；第二种为对像面（Image）前的最后一个面的曲率半径设置F数求解，将其中的F数设置为4。我们使用第二种方法，但F数的设置至少需要先构建好所有面的序列，所以F数的设置在后续操作中实现。我们首先将系统直径、视场、波长设置完成。

（3）全场视角为8度;

全场视角为8度意味着半场视角为4度，我们对视场角的设置会选用半场视角。题目中未限制视场个数与取法，我们首先介绍视场的取法，视场的取法满足以下公式：

式中n为视场个数，例如视场个数为3时，视场的取法为：0视场、0.707视场、1视场；如视场个数为5时，视场取法为：0视场、0.5视场、0.707视场、0.866视场、1视场。但是我们习惯选用3个视场，并且惯用取法为：0视场、0.7视场、1视场。

我们打开视场数据编辑器，点击三次insert，对三个视场进行命名（标注）为0视场、0.7视场、1视场，并设置它们的视场角为0、2.8、4，因为：

这些视场角设在Y角度上，X角度均为0。最后关闭视场数据编辑器。

打开视场数据编辑器

插入三个视场

加入标注

设置视场角度

（4）工作波长为588nm;

双击系统选项中的波长/设置，修改波长为0.588，回车并点击关闭。

打开波长数据

直接修改波长为0.588并回车

三大基本设置（系统孔径、视场、波长）到此完成，下面完成对成像系统镜面的搭建。

（5）材料为光学玻璃和光学塑料;

对于材料的选择题目没有对具体型号提出要求，我们可以选择最常用的BK7玻璃。

（6）学号尾号为双数的同学：光阑到第一个光学面的距离范围为2mm-6mm，透镜中心厚度为5.00-10.00mm;

（7）学号尾号为单数的同学：光阑到第一个光学面的距离范围为6mm-10mm，透镜中心厚度为10.00-15.00mm;

我的学号尾号为双数，选做第（6）项。因为本题为《单透镜的优化设计》，故至此可以确定好我们的成像系统的表面序列。一共有5个表面，分别为物面、光阑面、透镜前表面、透镜后表面、像面。示意图如下：

单透镜成像系统表面序列示意图

接着以此添加所有表面，并修改标注：

添加表面

修改标注

修改透镜的材料为BK7，修改的位置要在透镜前表面的一行，同样道理，对于任意两个表面之间的区间的材料、厚度均在这个区间的前表面那一行设置。

设置透镜的材料为BK7玻璃

当表面创建完成可以调出几个基本的可视化窗口：2D视图、标准点列图、光线像差图（光线光扇图）、光程差图，也可以提前将评价函数编辑器调出，直接对窗口布局好。点击设置/窗口/窗口布局/平铺所有窗口。

调出2D视图

调出标准点列图

调出光线像差图

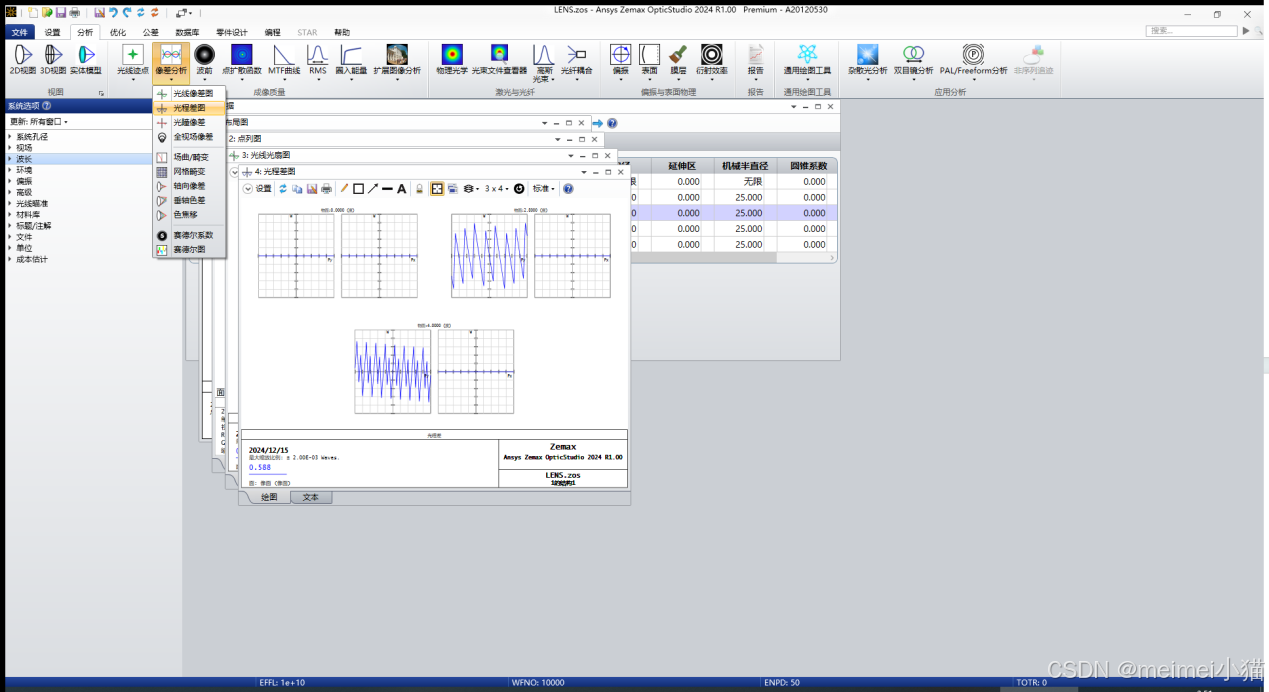
调出光程差图

调出评价函数编辑器

窗口布局

设置系统的F数，通过对像面前的最后一个表面的曲率半径使用F数求解来约束整个系统的F数，使得在系统孔径为50.00mm时，焦距（EFFL）为200.00mm。

设置F数为4

操作界面最下方

在操作界面的最下方我们可以看到EFFL的值为200，也就是焦距为200mm，我们可以以此对单透镜成像系统的几个值进行初始的合理设定。对于透镜后表面的厚度，即透镜后表面到像面的距离，可以设定为与焦距接近的值，我们设置为200mm。

透镜后表面厚度设置为200mm

对于透镜的厚度，因为入瞳直径为50.00mm，故透镜的厚度取5mm较为合适。

透镜厚度取5mm

光阑到透镜前表面有一定的距离，按照题目要求可先暂时设置为3mm。

光阑到透镜前表面距离设置为3mm

先重新优化一下窗口布局。

重新优化窗口布局

至此我们完成了一项工程“三步走”中的前两个步骤：“设置”和“分析”，而第三个步骤为“优化”。在优化之前，我们先对未优化的系统示意图和各个参数进行简单的分析。在我们打开的几个窗口中，我们可以首先关注点列图窗口：

点列图1

这是目前点列图的绘图报告，我们注意到上面有我们所设置的3个视场，并分别对应了其RMS半径，在优化过程中，RMS半径越小代表系统优化越完美。为了显示另一个参数艾里斑，我们打开设置并勾选显示艾里斑。

勾选显示艾里斑

这是目前点列图的文本报告：

点列图数据列表

文件 : C:\Users\IIP123\Documents\Zemax\SAMPLES\LENS.zos

题目:

日期 : 2024/12/15

角（度）

像单位: 毫米

参考: 主光线

参考: 主光线

面    : 像

波长:           值  权重

          0.588000 1.00

                                   X                Y

视场坐标  :   0.00000000E+00   0.00000000E+00

像坐标  :   0.00000000E+00   0.00000000E+00

RMS光斑半径   :   1.12020349E+03 µm

RMS X方向光斑尺寸   :   7.92103481E+02 µm

RMS Y方向光斑尺寸   :   7.92103481E+02 µm

最大光斑半径   :   1.82760199E+03 µm

视场坐标  :   0.00000000E+00   2.80000000E+00

像坐标  :   0.00000000E+00   9.78038268E+00

RMS光斑半径   :   1.22956189E+03 µm

RMS X方向光斑尺寸   :   8.26256660E+02 µm

RMS Y方向光斑尺寸   :   9.10561572E+02 µm

最大光斑半径   :   2.66140145E+03 µm

视场坐标  :   0.00000000E+00   4.00000000E+00

像坐标  :   0.00000000E+00   1.39817101E+01

RMS光斑半径   :   1.33857721E+03 µm

RMS X方向光斑尺寸   :   8.61480019E+02 µm

RMS Y方向光斑尺寸   :   1.02451995E+03 µm

最大光斑半径   :   3.09915108E+03 µm

光线光扇图1

这是目前光线光扇图（光线像差图）的绘图报告，由于ZEMAX软件原因，导致导出的图像模糊，但是我们的关注点主要在三个视场所绘制出的线形。对于优化至最完美的成像系统，图中的蓝色线条应该完全与横坐标轴重合，也就是曲线越接近横轴代表聚焦得越好。这是目前光线光扇图（光线像差图）的文本报告过于冗长，不再展示。

光程差图1

这是目前光程差图的绘图报告，其观察方法与光线像差图一致，不过多赘述，同时其文本报告也过于冗长，不再展示。

对于透镜的布局我们可以从2D视图、3D视图和实体模型来观察。对于3D视图和实物模型我们均给出了Y-Z、X-Y剖面和等轴测视图：

2D视图1

三维布局图1Y-Z

三维布局图1X-Y剖面图

三维布局图1等轴测视图

实体模型1Y-Z

实体模型1X-Y剖面图

实体模型1等轴测视图

从二维布局图、三维布局图和实体模型中我们都不难发现，优化前的单透镜系统的聚焦性还比较差，结合标准点列图中的最大视场RMS半径为1338.58，我们需要对这个单透镜系统进行优化，并实时关注上述这些分析量的变化。

（8）设计目标为SpotDiagram的均方根半径在近轴像面小;

为了设计好优化函数，我们需要设定一系列变量，并按照第（6）问的要求限制这些变量的变化范围。由于我们先前对透镜后表面的曲率半径进行了F数求解的条件限制，于是我们可以确定选择这些量作为变量：光阑面到透镜前表面的空气厚度、透镜前表面的曲率半径、透镜的厚度、透镜后表面到像面的距离。我们将这些参数设置为变量V，如图：

设置变量前

设置4个变量

将变量设置完成后我们可以开始设置优化函数。首先点开优化函数编辑器中的优化向导：

点开优化向导

优化函数中进行如下选择：成像质量选点列图、类型选RMS、参考选质心。因为设计目标为“SpotDiagram的均方根半径在近轴像面最小”。

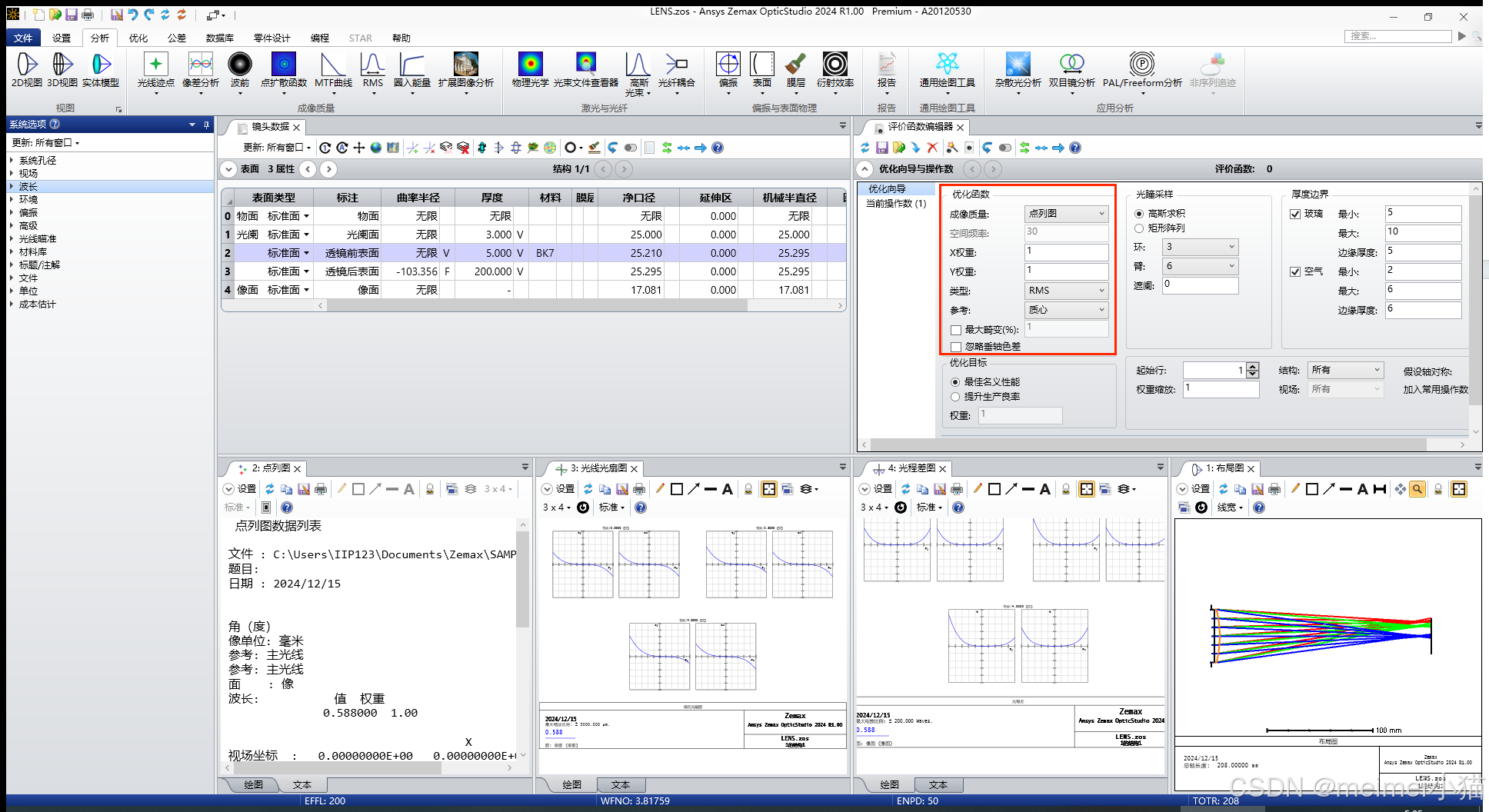
优化向导中的优化函数选择

光瞳采样选用高斯求积，超参数定位3环6臂，遮阑取0。也可取4环8臂，优化效率更高。这一步的高斯求积为一种优化算法。

优化向导中的光瞳采样

对于厚度边界，第（6）问要求光阑到第一个光学面的距离范围为2mm-6mm，透镜中心厚度范围为5.00mm-10.00mm。于是我们应该将玻璃厚度设置为最小为5、最大为10、边缘厚度为5，而玻璃厚度可以设置为最小为2、最大为6、边缘厚度为6。设置完成后点击确认，获得一系列的优化函数操作数。

获得优化函数操作数

此时有个比较重要的细节，即此时的操作数实际上是错误的，因为我们在设置厚度边界的时候并没有制定设置哪几个区间的厚度，如果此时不对厚度边界的操作数进行修改，则会得到错误的优化结果。对于厚度边界的操作数我将一一介绍：MNCA、MXCA、MNEA分别为最小空气厚度、最大空气厚度、空气的边缘厚度；MNCG、MXCG、MNEG分别为最小玻璃厚度、最大玻璃厚度、玻璃的边缘厚度。当我们鼠标选中厚度边界的某一行操作数，在列上就会出现对应的意义。

选中操作数

我们发现某一个操作数的面1和面2可以确定一个区间，而根据题目要求，我们显然是不需要这么多多余的操作数来限制其他区间变量的取值范围的，这会导致错误。所以我们需要将厚度边界操作数的区间修改到我们需要的范围上并删去多余的操作数。

对于光阑面到透镜前表面的空气厚度，我们只需将前三个操作数（MNCA、MXCA、MNEA）的面2都改为2即可，这表示了1表面到2表面这个区间，即光阑面到透镜前表面的空气厚度。对于透镜厚度，我们只需要将接下来三个操作数（MNCG、MXCG、MNEG）的面1改为2、面2改为3即可，这表示了2表面到3表面这个区间，即玻璃透镜的厚度。

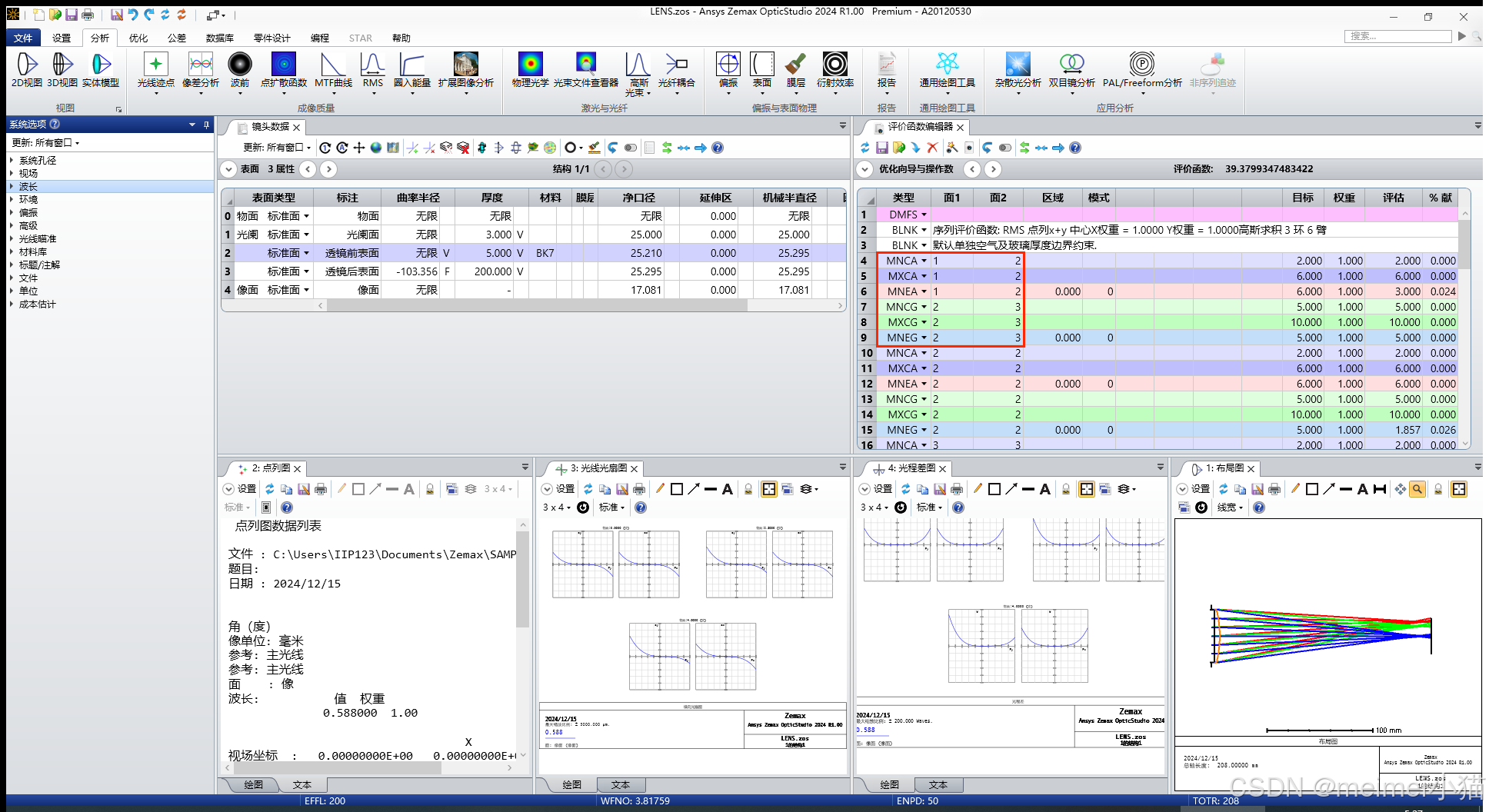
修改厚度边界操作数的区间

其余的有关厚度边界的操作数均要选中后右键删除。

删除多余厚度边界操作数

删除多余厚度边界操作数后

此时我们的评价函数已经设置好了，下一步可以直接优化。但我们先检查一下优化前题目剩余的要求。

（9）光学与结构参数均保留小数点后三位;

打开设置/OpticStudio选项，发现小数位已设置为3，符合要求。

打开设置/OpticStudio选项

设置小数位为3

（10）无其他限制；（以上仅采用球面光学面进行设计）;

每一个表面的表面类型，我们都设置为标准面，即为球面。

球面光学面

至此我们可以开始优化。点击优化/自动优化/执行优化。

点击执行优化

设置优化选项

在这几个选项中，我们按照如图示进行选择。迭代选自动。勾选自动更新（几个分析窗口可以实时变化），注意初始评价函数和当前评价函数的对比和变化。内核数目选择自己电脑CPU的线程数，按下Ctrl+Shift+Esc快捷键打开任务管理器，发现我们的CPU型号为Intel Core I9 10900KF，我们的逻辑处理器个数为20，故内核数目选20。

查看CPU

点击开始，开始优化。如图为优化后的界面：

优化后

可见优化后一些量发生了变化，首先初始评价函数为1.33，而当前评价函数变为了0.04，评价函数的大幅减小意味着这次优化是成功的。对于我们设置的4个变量：光阑面到透镜前表面的空气厚度从初始的3.000mm变成了6.000mm，优化后的这一变量符合问题（6）给出的要求，即光阑到第一个光学面的距离范围为2mm-6mm；透镜前表面的曲率半径从初始的无限变成了119.296mm；透镜的厚度从初始设置的5.000mm变成了9.999mm，优化后的这一变量符合问题（6）给出的要求，即透镜中心厚度范围为5.00mm-10.00mm；透镜后表面到像面的距离从初始设置的200.000mm变成了191.525mm。此外透镜后表面的曲率半径也受到F数求解的限制以维持EFFL的值保持为200mm，其值调整为了-751.445mm。

接下来再分别从几个分析窗口来观察优化后的系统状态。

对于标准点列图，优化后的图像如图所示：

点列图2

图像上，优化后的汇聚能力明显增强。指标上，可以发现最大视场RMS半径和GEO半径都得到了显著减小，最大视场的RMS半径减小超过十倍，这表明优化效果及其显著。但是艾里半径略微增大。以下是优化前后的点列图对比图：

点列图（优化前）

点列图（优化后）

对于光线光扇图（光线像差图），优化后的图像如图所示：

光线光扇图2

可以发现优化后的曲线更加均匀地分布在横轴的上下两侧，说明优化效果很好。以下是优化前后的光线光扇图对比图：

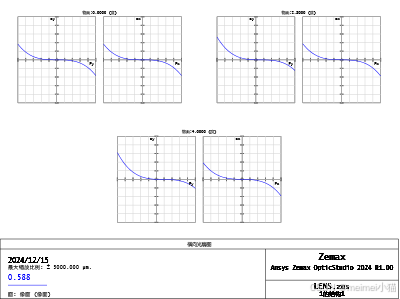
光线光扇图（优化前）

光线光扇图（优化后）

以下是优化前后的光程差图对比图：

光程差图（优化前）

光程差图（优化后）

以下是优化前后的二维布局图对比图：

2D视图（优化前）

2D视图（优化后）

对比可见，优化后的焦点明显落在像面上，会聚能力更强：

以下是优化前后的三维布局图对比图：

三维布局图Y-Z（优化前）

三维布局图Y-Z（优化后）

三维布局图X-Y剖面图（优化前）

三维布局图X-Y剖面图（优化后）

三维布局图等轴测视图（优化前）

三维布局图等轴测视图（优化后）

以下是优化前后的实体模型对比图：

实体模型Y-Z（优化前）

 实体模型Y-Z（优化后）

实体模型X-Y剖面图（优化前）

实体模型X-Y剖面图（优化后）

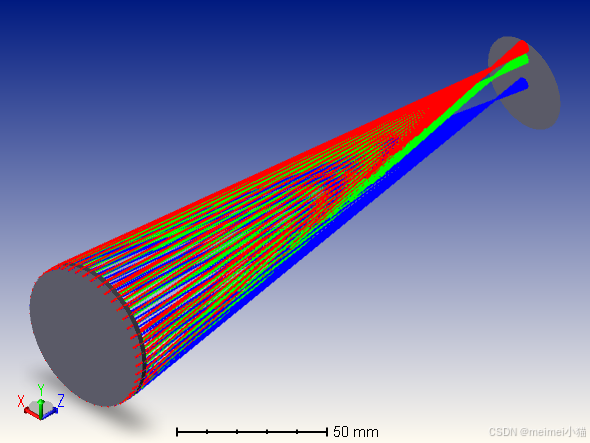
实体模型等轴测视图（优化前）

实体模型等轴测视图（优化后）

---

2.设计结果

（1）2D和3D系统图

2D系统图

3D系统图

（2）系统参数数据（Prescription Data）及评价（下述内容以表格或者图的形式给出）；

系统参数数据：

系统/详细数据

文件 : C:\Users\IIP123\Desktop\Zemax_Homework\单透镜的优化设计\ZEMAX文件\Single Lens.zos

题目:

日期 : 2024/12/15

常用透镜数据:

面                      :                4

光阑                    :                1

系统孔径                : 入瞳直径 = 50

半口径快速计算           : on

视场无偏振               : On

将膜层相位转化为等效几何光线              : On

J/E 转化方法            : X轴参考   

玻璃库                   : SCHOTT

光线瞄准                : 关

切趾法                  : 均匀,因子 =    0.00000E+00

OPD参考                 : 出瞳  

近轴光线                : 忽略坐标断点  

F/#计算                 : 追迹光线  

惠更斯积分计算   : 自动

显示坐标断点             : on

多线程                  : on

OPD以2π取模             : off

温度 (℃)               :     2.00000E+01

压强 (ATM)              :     1.00000E+00

折射率数据与环境匹配     : off

有效焦距                :              200 (在系统温度和压强的空气中)

有效焦距                :              200  (在像方空间)

后焦距                  :         194.0735

总长                    :         209.3988

像方空间 F/#            :                4

近轴处理 F/#            :                4

工作F/#                 :         4.001412

像方空间 NA             :        0.1240347

物方空间 NA             :          2.5e-09

光阑半径                :               25

近轴成像高度            :         13.98536

近轴放大率              :                0

入瞳直径                :               50

入瞳位置                :                0

出瞳直径                :          51.7295

出瞳位置                :        -206.2433

视场类型                : 角（度）

最大径向视场            :                4

主波长                  :            0.588 μm

角放大率                :        0.9665665

透镜单位                :             毫米

光源单位                 :    瓦特

分析单位                :    瓦特/cm^2

无焦模式单位             :    毫弧度

MTF 单位                :    周期/毫米  

计算数据保存于Session文件                 : On  

计算数据保存于Session文件                 : On  

视场         : 3

视场类型                : 角（度）

 #      X-角度        Y-角度          权重

 1       0.000000       0.000000       1.000000

 2       0.000000       2.800000       1.000000

 3       0.000000       4.000000       1.000000

渐晕因子

 #      VDX      VDY      VCX      VCY      VAN

 1  0.000000  0.000000  0.000000  0.000000  0.000000

 2  0.000000  0.000000  0.000000  0.000000  0.000000

 3  0.000000  0.000000  0.000000  0.000000  0.000000

波长    : 1

单位: μm

 #         值           权重

 1       0.588000       1.000000

预测坐标 ABCD 矩阵:

A =        199.3

B =            0

C =            0

D =        199.3

  

*General Lens Data

镜头数据

*Filed

全视场像差

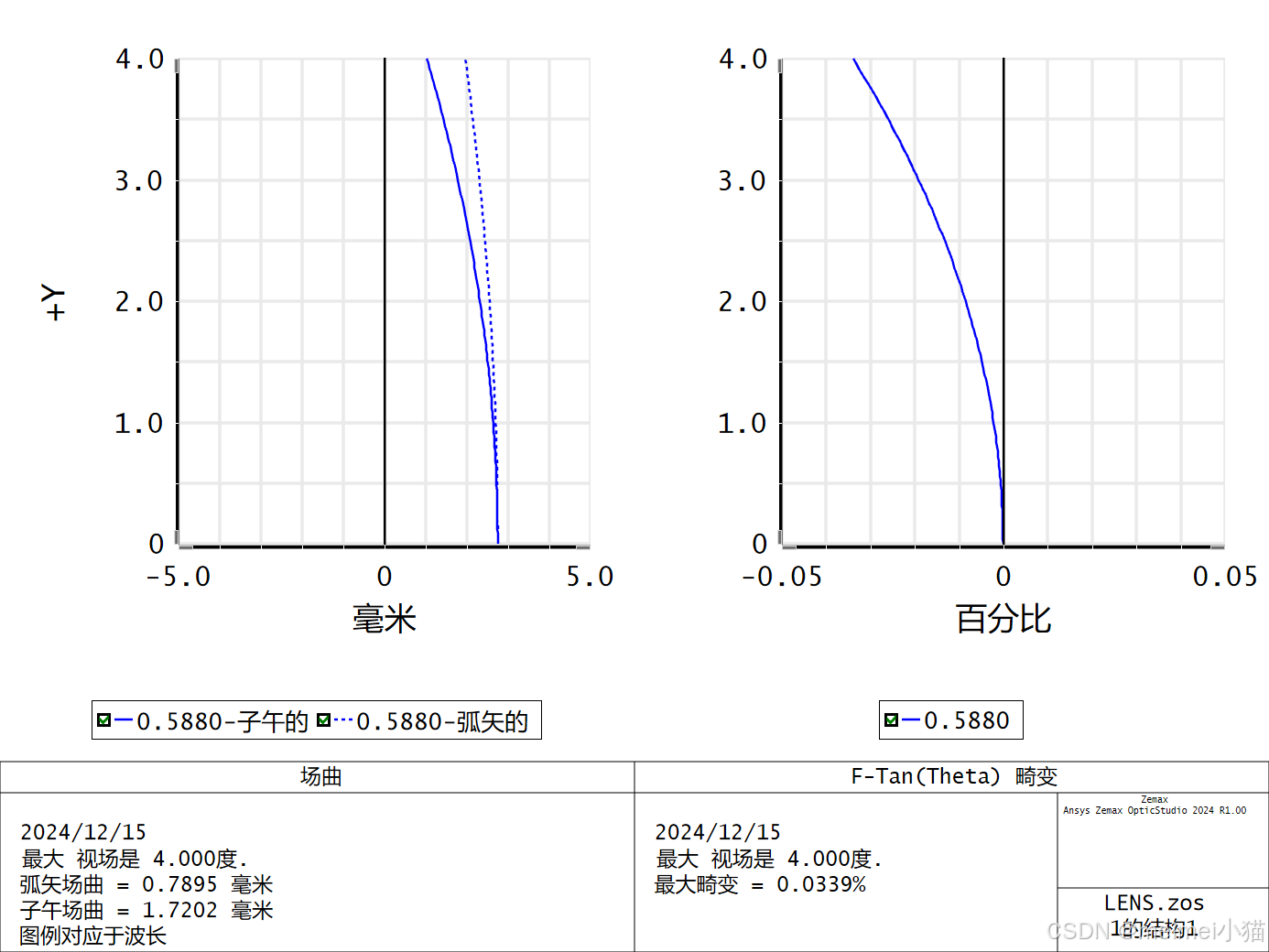
视场场曲畸变

FFTMTFvs视场

惠更斯MTFvs视场

几何MTFvs视场

*Wavelength

RMSvs波长

*Surface Data Summary

表面	注释	厚度 (mm)	直径 (mm)	Y 边缘厚度 (mm)	X 边缘厚度 (mm)	玻璃类型	波长 1 (折射率)	波长 2 (折射率)	波长 3 (折射率)
1	光阑面	5.99995	50.000	8.89107	8.89107	-	1.0000000000	-	-
2	透镜前表面	10.000	51.2434	6.81142	6.81142	BK7	1.5167817368	-	-
3	透镜后表面	193.399	50.8054	193.696	193.696	-	1.0000000000	-	-
4	像面	0.000	28.185	0.000	0.000	-	1.0000000000	-	-

*Spot Diagram

*RMS vs Field Plot

RMSvs视场

---

1.设计参数与要求

（11）进一步，利用单个非球面提升单透镜的性能，并输出结果。

2.设计结果

（3）分析对比仅采用球面光学设计与引入非球面设计前后单透镜光学系统的成像质量变化。

在球面光学系统优化的基础上，我们引入偶次非球面，代替透镜前后表面中的某一个，以实现非球面光学系统的设计，如图是先前的球面光学系统：

球面光学系统

我们将透镜后表面的表面类型更改为偶次非球面，并设置非球面的高阶项为变量，这里只设置2阶项和4阶项。

更改为偶次非球面

设置偶次非球面的高阶项为变量

点击执行优化：

进行非球面优化

引入了非球面设计并进行了优化后，评价函数从原来的0.043降到了0.027。镜头数据中的偶次非球面透镜后表面的高阶项：2次项从0变成了-4.150E-03，4阶项从0变成了1.717E-08。其他镜头数据也发生了如图变化：

非球面优化的参数变化

对于分析窗口，我们将依次比较仅采用球面光学设计与引入非球面设计的前后成像变化。

如图展示了仅采用球面光学设计与引入非球面设计的前后标准点列图对比图：

仅使用球面优化设计的点列图

引入非球面优化设计的点列图

我们发现引入了非球面设计后，最大视场的RMS半径又进一步从132.539减小到了76.692，这证明引入非球面设计可以进一步优化仅使用球面的光学系统优化设计。

仅使用球面优化的光线光扇图

引入非球面优化的光线光扇图

仅使用球面优化设计的光程差图

引入非球面优化设计的光程差图

仅使用球面优化设计的2D视图

引入非球面优化设计的2D视图

仅使用球面优化的三维布局图Y-Z

引入非球面优化的三维布局图Y-Z

仅使用球面优化的三维X-Y剖面

引入非球面优化的三维X-Y剖面

仅使用球面优化的三维等轴测视

引入非球面优化的三维等轴测视

仅使用球面优化的实体模型Y-Z

引入非球面优化的实体模型Y-Z

仅使用球面优化的实体X-Y剖面

引入非球面优化的实体X-Y剖面

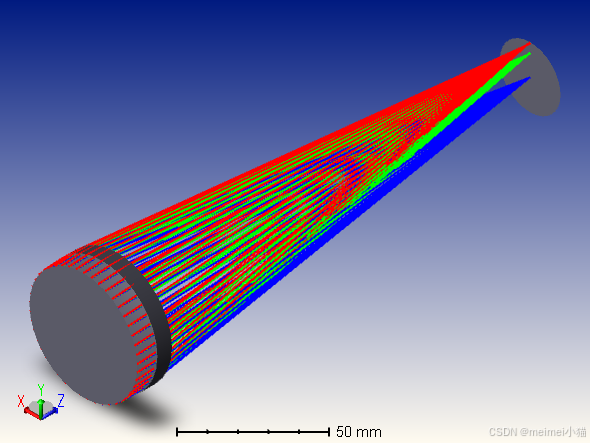
仅使用球面优化的实体等轴测视

引入非球面优化的实体等轴测视

对于2D布局图和3D布局图，引入非球面优化设计前后变化不明显，不易察觉。

综合上述对比，在引入了非球面优化设计后，评价函数从原来的0.043降到了0.027，同时最大视场的RMS半径也进一步从132.539减小到了76.692，这证明引入非球面设计可以进一步优化仅使用球面的光学系统优化设计。

3.阐述单透镜设计过程中关键参数计算及其优化设计思路（Tips和Tricks）（字数不限）

1.系统设计第一步是“设置”，包括设置系统孔径、视场、波长，也包括设置约束条件的F数求解。其中系统孔径的注意点是，其数值等于焦距（EFFL）除以F数；视场的注意点是，视场的选取有固定的方法，一般选用0视场、0.7视场和1视场，视场角的大小为半视场角乘0、0.7或1；波长的设置可以是一个数，也可是一个范围；F数的设置有两种方法，第一种是根据系统F数与入瞳直径（系统孔径）的乘积算出焦距（EFFL）（焦距或者入瞳直径其中的一个量会直接给出），然后再优化函数的操作数中添加EFFL操作数，将其目标值定位我们依据F数计算出的焦距或者给出的焦距，并将权重设为1。第二中方法是对像面前的最后一个表面的曲率半径添加F数求解的约束条件。

2.系统设计的第二步是“分析”，为了分析系统当前状态并比较优化前后的状态变化以评估优化的好坏，我们会调出几个常用的分析窗口：标准点列图、光线光扇图（光线像差图）、光程差图、二维布局图（也可查看三维布局图和实体模型）。标准点列图中我们主要关注各视场的像点分布图像和最大视场的RMS半径和GEO半径，对于效果比较完美的优化设计，0视场的像点应该分布地均匀且集中，其代表中心成像质量。0.7视场和1视场代表边缘成像质量，理想状态下，它们的像点也应该集中分布；对于光线光扇图（光线像差图），较为理想状态下曲线应该均匀分布在横轴两侧且靠近横轴；对于光程差图，较为理想的状态下曲线应该尽可能靠近横轴；对于二维布局图、三维布局图和实体模型，我们主要关注透镜的形态，以及所有视场的焦点是否正好落在像面上。

3.系统设计的第三步是“优化”，我们首先需要确定优化变量（设置了F数求解约束条件的参数我们不要选择），然后通过评价函数编辑器中的优化向导操作来自动生成操作数并做相应的修改。优化向导中的优化函数要根据我们的设计目标来设定，光瞳采用是优化算法及其超参数的选定，厚度边界的设定是初步的，具体对哪些区间进行厚度边界的设定需要手动对操作数进行修改。优化后我们需要关注镜头数据的各个参数变量的变化以及分析窗口评价指标和评价函数的变化。需要仔细检查我们对厚度限制的变量是否在设定范围内，二维布局图中的透镜形态和焦点落点是否正常，标准点列图中所有视场的像点是否会聚等。主要的评价指标我们关注最大视场的RMS半径和GEO半径是否减小，如果显著减小说明优化效果和成像质量都很高，评价函数最理想的状态为0，如果评价函数减小说明此次优化有效。

4.非球面优化：仅仅使用球面光学面进行设计的最佳优化性能有限，我们可以引入一个或多个非球面，我们常使用偶次非球面。可将像面前的最后一个表面的表面类型从标准面改为偶次非球面，此时在镜头数据编辑器中会出现这个偶次非球面的高阶项，我们将一些高阶项（通常只设置2阶项和4阶项等）设置为变量，并直接局部优化，可以发现评价函数进一步下降，各项评估指标进一步优化。除了使用局部优化，我们也可使用锤型优化以突破局部最优，试图在足够长的时间内找到全局最优解。