单变量微积分（02）：Derivatives, Slope, Velocity, and Rate of Change

1. 导数的几何意义

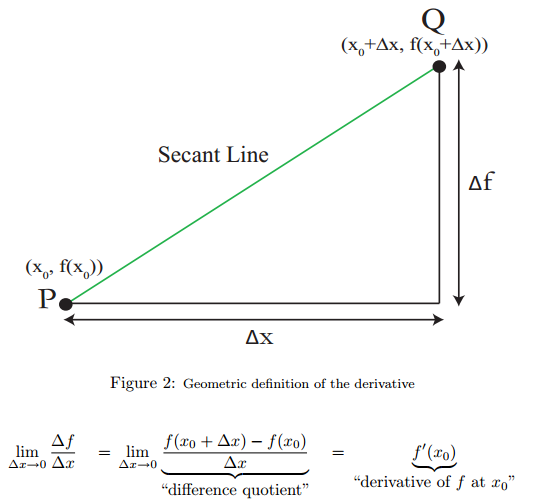
函数$f(x)$在点$P$的导数定义为$P$点在函数曲线上的该点切线的斜率。但是如何来准确的求出曲线在该点的切线呢。

有两点要注意：

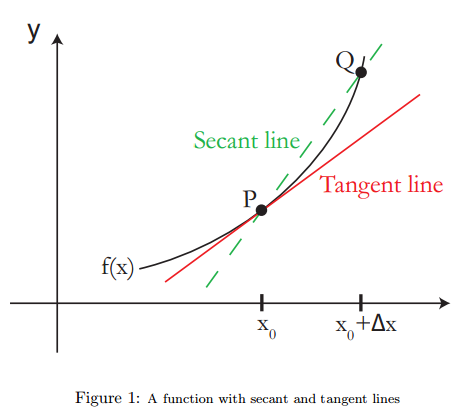
• 切线并不是只与曲线只有一个交点的线
• 它是曲线上另一点逐渐靠近$P$点时，形成的割线斜率的极限。

所以导数的几何定义即为：

Limit of slopes of secant lines $PQ$ as $Q\to P$($P$ fixed). The slope of $\overline{PQ}$:

在我们知道了曲线的导数$f'(x)$后，我们可以求得点$P(x_0,y_0)$处的切线方程为：

$$y-y_0 = f'(x)(x-x_0)$$

一些记号

由于$y=f(x)$，所以我们记：

Δy