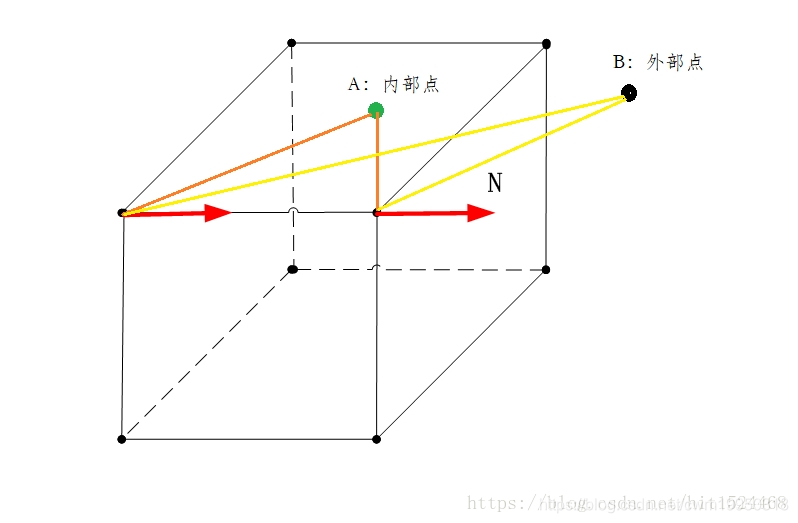
几何解释
如下图所示，我们其实只需要判断一个点是否在3组平行平面的同一侧即可以判断(前/后面，左/右面，上/下面)，判断的方法比较简单：即利用如图所示中的与法线的夹角，当一个点(如图中点B)在左右面的同一侧时，与法线的夹角都是锐角或钝角；当一个点(如图中点A)在左右面的不同侧时，与法线的夹角必定一个为锐角一个为钝角；实际上，我们不需要判断角度，我们只需要判断余弦值的符号即可，即可以判断向量的内积的符号即可。
判断点是否在两个平行面的同一侧 <=> 判断点与法线的夹角的大小 <=> 判断余弦值的符号 <=> 判断向量内积的符号
引用自：判断点是否包含在任意姿态长方体内部
数学工具
平面方程的一般形式为：
A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0
假设 D ≠ 0 D\neq0 D=0，将 D D D移至 = = =右边，所有系数除以 D D D，并乘以 − 1 -1 −1，公式可写为：
A x + B y + C z = 1 Ax+By+Cz=1 Ax+By+Cz=1
三个不共线的点确定一个平面
假设已知不共线三点： ( x 1 , y 1 , z 1 ) ， ( x 2 , y 2 , z 2 ) ， ( x 3 , y 3 , z 3 ) (x_{1},y_{1},z_{1})，(x_{2},y_{2},z_{2})，(x_{3},y_{3},z_{3}) (x1,y1,z1)，(x2,y2,z2)，(x3,y3,z3)，可列出一组三元一次方程：
A x 1 + B y 1 + C z 1 = 1 A x 2 + B y 2 + C z 2 = 1 A x 3 + B y 3 + C z 3 = 1 Ax_{1}+By_{1}+Cz_{1}=1\newline Ax_{2}+By_{2}+Cz_{2}=1\newline Ax_{3}+By_{3}+Cz_{3}=1 Ax1+By1+Cz1=1Ax2+By2+
最低0.47元/天 解锁文章
3161
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
