入门级深度神经网络 with Pytorch(3) - 线性网络（二）

cy448219947

已于 2023-08-28 22:04:06 修改

阅读量46

点赞数

文章标签： dnn pytorch 人工智能

于 2023-08-28 21:59:51 首次发布

本文链接：https://blog.csdn.net/cy448219947/article/details/132546018

版权

前言

上一篇内容：入门级深度神经网络 with Pytorch(2) - 线性网络（一）

在上一篇内容中，我们介绍了最基本的由 $y = w x$ 为基础的数据集进行的单线性网络层模型的训练。不知道大家对其吸收的如何了呢？上篇我们留下了一个悬念，那就是对于 $y = w x + b$ 为基础组成的数据，它的底层训练逻辑又有些什么扩展呢？

代入场景

我们再次代入挖金矿的场景，由于在市场上流通的黄金实在太多，太碎太小的黄金已然变得不值钱。只有开采到一定重量的金矿石，你才能卖出一个价格。于是你又记录了一次当前的市场下，金矿石的重量和可卖出的价格之间的关系，如下图所示：
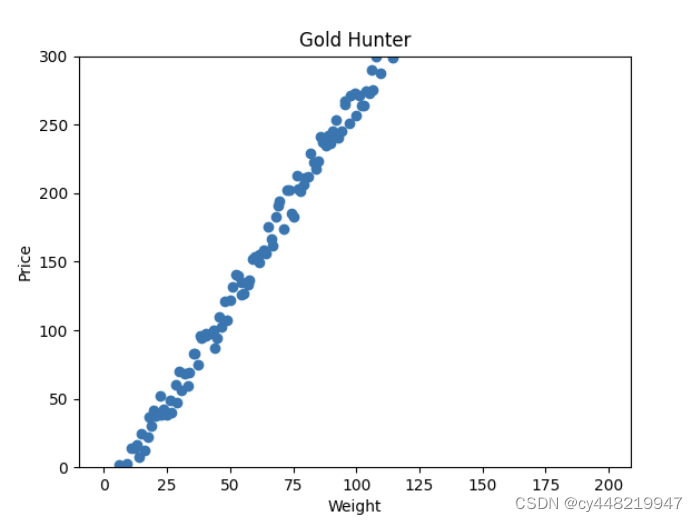
金矿石重量和价格关系图

可以看到，直到金矿石达到了一定的重量，市场才认可它是有价值的。很显然，我们已经不能再像之前那样去预测我们挖到金矿的价格了，那应该怎么办呢？我们是时候更新我们的模型了。

理论

我们还是一步一步地对模型训练时的每一个过程进行推导。

前向传播

这次我们还是先遵从我们的直觉，从这个数据分布来看，这次我们应该要用一个 $y = w * x + b$ 的直线来对我们现在的数据集进行描述。
和往常一样，我们先随便猜了一个w和b的取值，比如是1和-1，于是我们现在的预测直线就是 $y = 1 * x - 1$
好，我们迫不及待地随机拿出一块石头，发现它重量是30.4，于是我们计算出这块石头的预测重量应该是 $1 * 30.4 - 1 = 29.4$
又一次，我们完成了我们的前向传播。

损失计算 —— w

我们查了一下我们的数据表，发现这块石头真正的价格是56.2，欧我的老伙计，这可不太妙。但由于有了以往的经验，我们并不是特别慌张，我们祭出了我们已经熟练使用的老朋友——均差方损失函数来对我们这次的损失进行计算。
这次我们多了一个参数b，但没关系，我们先假设b是一个定值，而w是自变量，来得到我们的计算公式：
$G_{loss}=(y_{0} - (x_{0}*w+b))^{2}$
我们对这个二次项进行展开，可以得到：
$G_{loss}=x_{0}^{2}w^{2}-2*x_{0}*(y_{0}-b)*w + (y_{0}-b)^2$
注意，这里的b，我们姑且认为它是一个定值，而不是变量。基于这个前提，我们发现这个损失函数仍旧是一个w为自变量的开口向上的抛物线。
也就是说，我们给定了x, y, b的值的前提下，我们仍旧可以算出w当前的一个损失。

损失计算 —— b

接着，我们看看b。现在我们转换一下，假设w是一个定值，而b是自变量，我们可以看看展开的公式变成了什么样：
$G_{loss}=b^{2}-2*(y_{0}-x_{0}*w)*b + (y_{0}-x_{0}*w)^{2}$
这就很nice了，我们可以看到w是定值的情况下，我们得到的损失函数，是一个关于b的开口向上的抛物线。它还是一样的抛物线。

梯度下降

接下来是需要大家进行一个三维空间想象的环节。我们现在建立这样一个三维坐标系：横坐标x轴是变量w，纵坐标y轴是损失G_loss，然后我们在垂直于xy轴的方向作一条z轴，代表变量b。
由上面的推导我们知道，对于定值b，w是一个个开口向上的抛物线，而对于定值w，b也是一个个开口向上的抛物线，那在三维空间里，它会是一个怎么样的图形呢？引用网上找到的图，它应该是长这样的：
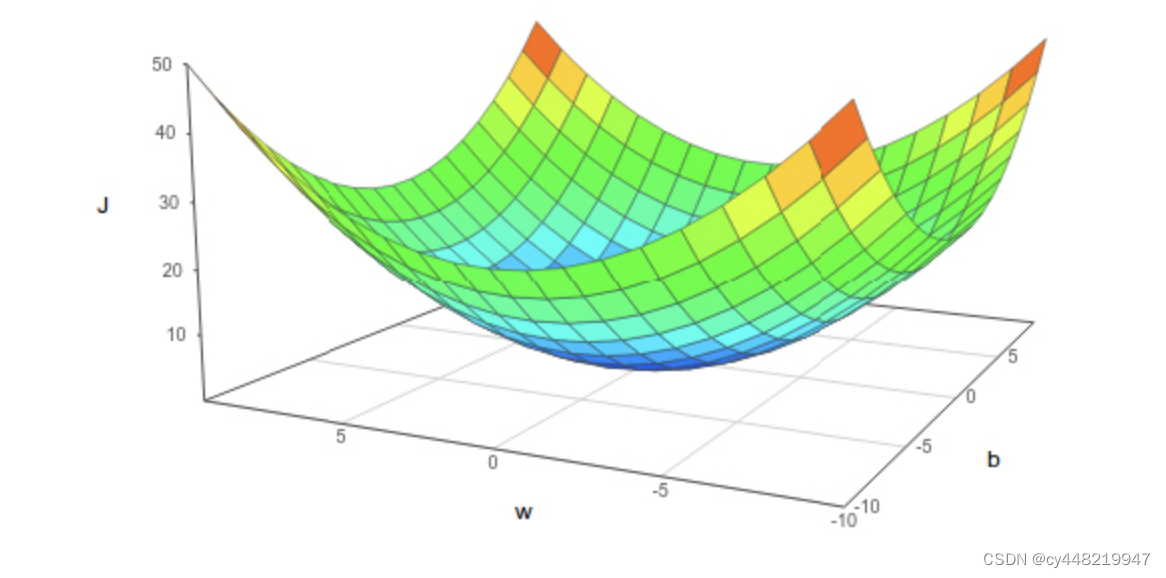
搜索引擎找到的图，如有侵权请告知我我会删除
这是一个有点类似一个碗的图形，我们把它横着切开（固定w），或者竖着切开（固定b）看截面，它都应该是一条开口向上的抛物线。
现在如果我们要让损失尽可能的低，那么很显然，我们就要让w和b向这个碗的最低点移动。
移动的策略非常简单，我们在固定b的情况下，由于G_loss与w的图形就是个开口向上的抛物线，我们仍旧让w减去当前切线的斜率乘学习率alpha即可：
$w_{n+1}=w_{n}-alpha*k_{n}$
$k_n=2*c*w_n +d$
其中
$c=x_{0}^{2}+x_{1}^{2}+...+x_{m}^{2}$
$d=-2*(x_{0}(y_{0}-b_{n}) +x_{1}(y_{1}-b_{n})...+x_{m}(y_{m}-b_{n}))$
如此代入所有值，我们便可计算出梯度下降后的w。
然后对于b我们则将w固定，用同样的方法，进行一次梯度下降：
$b_{n+1}=b_n-alpha*k_n$
$k_n=2*b_n+c$
其中
$c=2*((y_{0}-x_{0}*w_n) + (y_{1}-x_{1}*w_n) + ... + (y_{m}-x_{m}*w_n)$
代入所有值后，梯度下降后的b我们也就算出来了。有一个事情是要注意的，我们先计算了w，得到了下一个w(n+1)，但是我们在计算b时，仍旧应该代入w(n)，而不是w(n+1)。

反向传播

既然我们已经计算出了新的w和b，我们擦除旧的w和b，替换上新的就可以了。我们的一个batch的训练也就这么完成了。接着我们便一遍遍把batch数据送入，一次次得到更加好的w和b，就能让我们的预测模型越来越准确了。
相信在理解了上篇文章的前提下，本次的扩展的理解难度会降低不少，毕竟我们本身就掌握了梯度下降的精髓，当我们一看到开口向上的抛物线的时候，我们就能一下子反应过来应该要怎么做。

代码实践

ok，既然理论已经了解完了，那我们便直接进入pytorch的代码实践环节。本次的代码环节和上一次差的不太多，相同的地方我就一笔带过，不同的地方我会详加解释。

训练数据构造

这次的训练数据我们和上次稍有不同，一方面是多了一个截距b，另一方面我们把斜率稍微弄的低一些，以降低我们的训练难度：

import numpy as np
import random

def get_data(num):
    xs = []
    ys = []
    weight = 3
    bias = -30

    for i in range(num):
        x = i + random.randint(-4, 4) / 10
        # 这里我们加上截距b
        y = (weight) * x + random.randint(-15, 15) + bias
        xs.append(x)
        ys.append(y)

    X = np.array(xs)
    Y = np.array(ys)
    return X, Y

同样的，我们用matplotlib画出图形看一下：

from matplotlib import pyplot as plt

X, Y = get_data(total)

plt.title("Gold Hunter", fontsize=12)
plt.xlabel("Weight")
plt.ylabel("Price")
plt.ylim(0, 300)
plt.scatter(X, Y)

这次得到的数据大概长这样
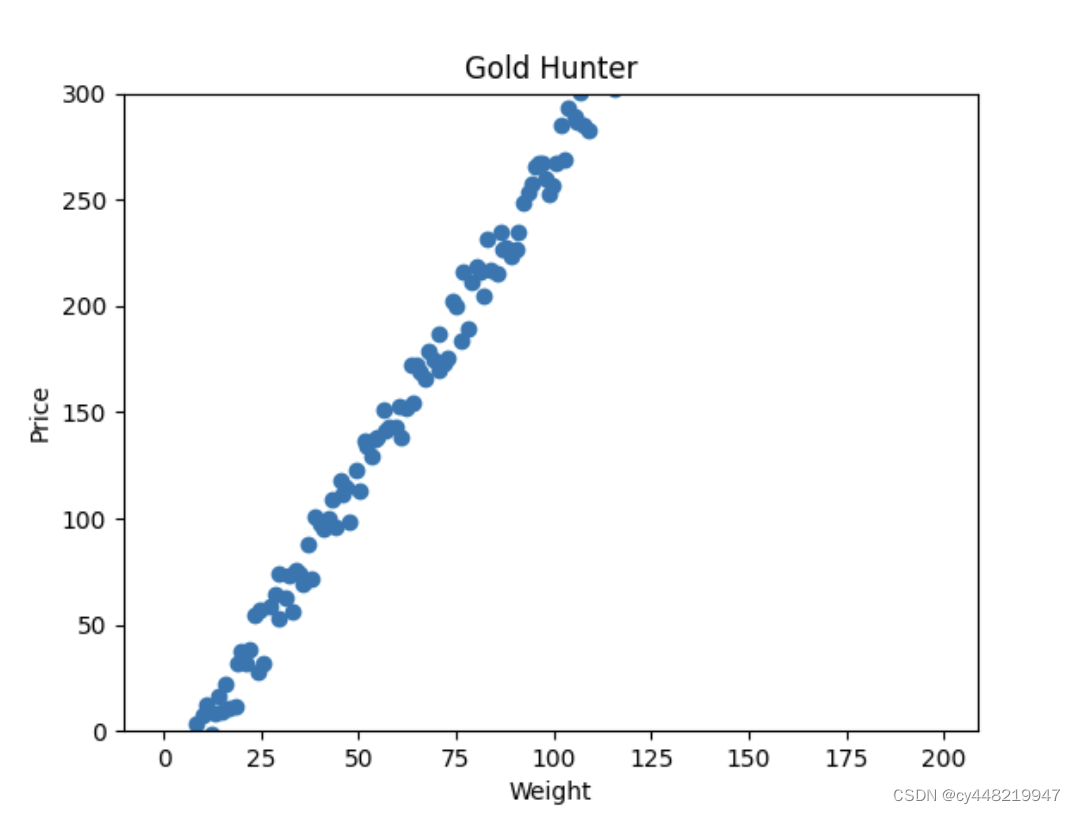
在这里插入图片描述
也与之前相同，我们把数据放入tensor中

import torch

train, result = torch.FloatTensor(X), torch.FloatTensor(Y)

神经网络搭建

神经网络的搭建和上一篇文章基本相同，在此就不多赘述了，我们直接上代码：

import torch.nn as nn

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # 构造一个出入皆为1维的线性层
        self.lc = nn.Linear(1, 1)

    def forward(self, x):
        output = self.lc(x)
        return output

import torch.optim as optim
from torch.nn import MSELoss

# 在这里，我们设学习率为0.00002
learning_rate = 2e-5

model = Net()
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
loss_function = MSELoss()

注意一下，这里学习率我略微调高了一点，否则之后会发现学习的效果并不是特别好。

开始训练

好了，万事俱备，只欠训练。这次我们训练的时候需要多记一个参数，也就是截距b，我们需要把它记录下来来最后看下我们拟合出来的图线，其它的细节与我们之前基本都是完全一样的。

final_w = 0
final_b = 0
for i in range(int(total/batch_size)):
    data = train[i*batch_size:(i+1)*batch_size]
    target = result[i*batch_size:(i+1)*batch_size]
    optimizer.zero_grad()
    output = model(data)
    loss = loss_function(output, target)
    loss.backward()
    optimizer.step()

    grad = []
    for parameters in model.parameters():
        grad.append(parameters)

    final_w = grad[0].data[0][0]
    final_b = grad[1].data[0]

跑一次试试

我们加入我们的图形验证代码，来跑一次试试，看看是否做到了拟合：

y_pre = final_w * X + final_b
plt.plot(X, y_pre)
plt.show()

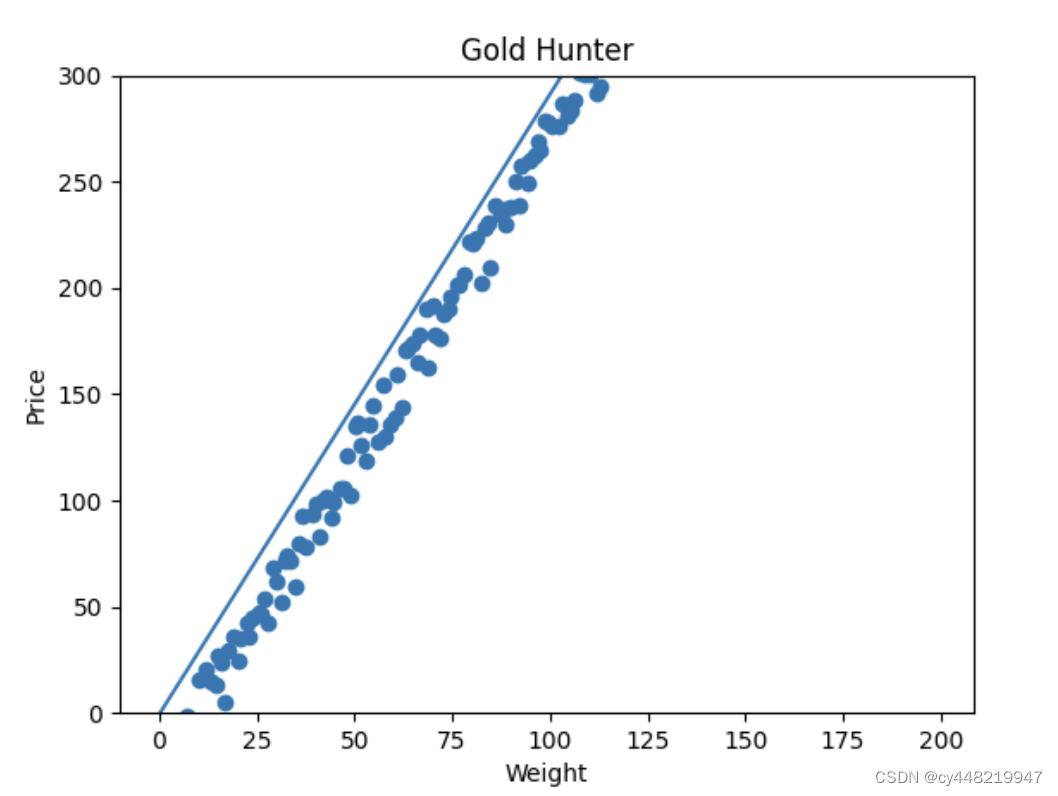
在这里插入图片描述
Emmm，总感觉有些差强人意，大致上是有些拟合出来的感觉了，但在截距上仍旧差了些。这时候我们应该怎么办呢？方法有两种：

调整我们的学习率，来让梯度下降的快一些或者慢一些。
更简单有效的办法，便是直接再跑几次，让模型针对我们的训练集再来几轮梯度下降，这样我们的参数拟合度不就越来越高了吗（也就是多跑几轮Epoch）
我们修改一下我们的训练代码，说是修改，其实就是外面再嵌套一个循环：

for x in range(2000):
    for i in range(int(total/batch_size)):
        data = train[i*batch_size:(i+1)*batch_size]
        target = result[i*batch_size:(i+1)*batch_size]
        optimizer.zero_grad()
        output = model(data)
        loss = loss_function(output, target)
        loss.backward()
        optimizer.step()

        grad = []
        for parameters in model.parameters():
            grad.append(parameters)


        final_w = grad[0].data[0][0]
        final_b = grad[1].data[0]

在这里我们直接简单暴力地让它跑2000轮，我们看看现在的效果
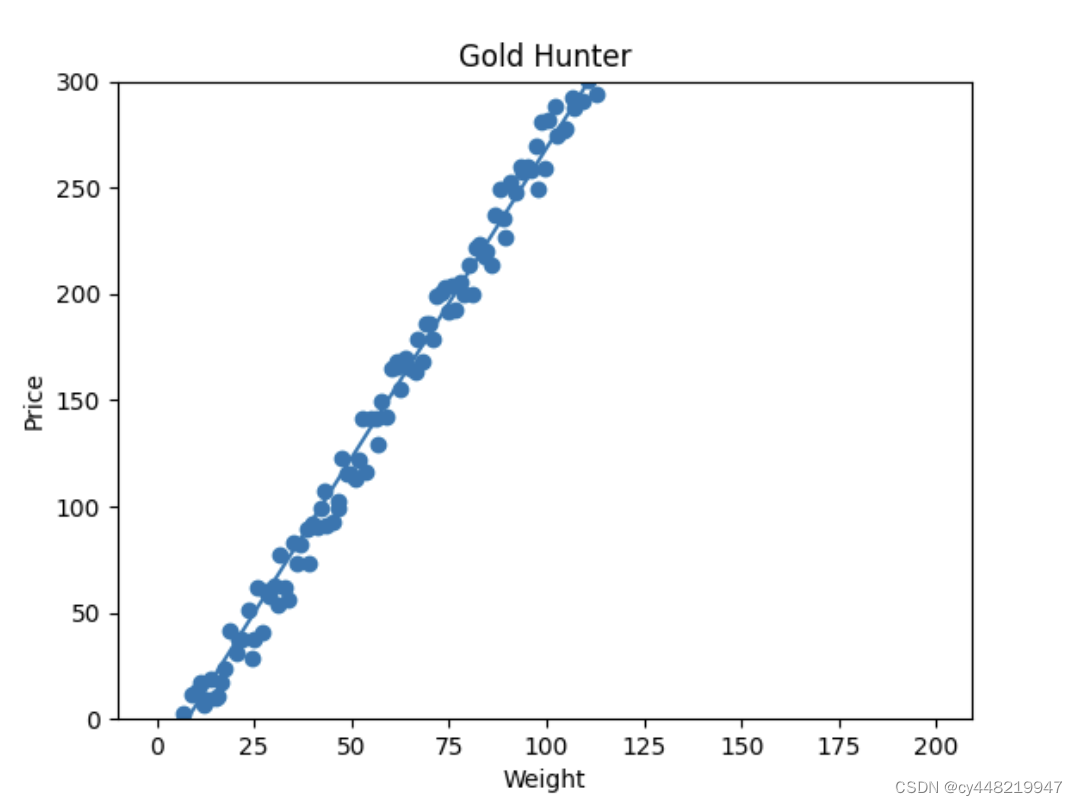
在这里插入图片描述
芜湖~非常好，现在的直线看起来就拟合的很完美了。

结语

好了，我们先来总结一下今天的文章的内容。在本次，我们对之前的直线引入了截距b，让我们的模型可以应对新的金矿卖钱场景。我们了解了在多了一个参数的情况下，如何对我们的网络层进行梯度下降，并通过pytorch代码对此进行了实践。
从下篇文章开始，我们要讨论一个更具有实际意义的问题——二元分类问题，我们会结识我们新的伙伴，激活函数。也敬请大家期待啦~

完整代码

import numpy as np
import random
import torch
from matplotlib import pyplot as plt
import torch.nn as nn
import torch.optim as optim
from torch.nn import MSELoss

batch_size = 1
learning_rate = 2e-5

def get_data(num):
    xs = []
    ys = []
    weight = 3

    for i in range(num):
        x = i + random.randint(-4, 4) / 10
        y = (weight) * x + random.randint(-15, 15) - 30
        xs.append(x)
        ys.append(y)

    X = np.array(xs)
    Y = np.array(ys)
    return X, Y


class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.lc = nn.Linear(batch_size, batch_size)

    def forward(self, x):
        output = self.lc(x)
        return output


if __name__ == "__main__":
    device = torch.device("mps")

    total = 200

    X, Y = get_data(total)

    plt.title("Gold Hunter", fontsize=12)
    plt.xlabel("Weight")
    plt.ylabel("Price")
    plt.ylim(0, 300)
    plt.scatter(X, Y)

    train, result = torch.FloatTensor(X), torch.FloatTensor(Y)

    model = Net()
    optimizer = optim.SGD(model.parameters(), lr=learning_rate)
    loss_function = MSELoss()

    final_w = 0
    final_b = 0

    for x in range(2000):
        for i in range(int(total/batch_size)):
            data = train[i*batch_size:(i+1)*batch_size]
            target = result[i*batch_size:(i+1)*batch_size]
            optimizer.zero_grad()
            output = model(data)
            loss = loss_function(output, target)
            loss.backward()
            optimizer.step()

            grad = []
            for parameters in model.parameters():
                grad.append(parameters)


            final_w = grad[0].data[0][0]
            final_b = grad[1].data[0]

    print(final_w)
    print(final_b)
    y_pre = final_w * X + final_b
    plt.plot(X, y_pre)
    plt.show()

cy448219947

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
1
评论
入门级深度神经网络 with Pytorch(3) - 线性网络（二）

好了，我们先来总结一下今天的文章的内容。在本次，我们对之前的直线引入了截距b，让我们的模型可以应对新的金矿卖钱场景。我们了解了在多了一个参数的情况下，如何对我们的网络层进行梯度下降，并通过pytorch代码对此进行了实践。从下篇文章开始，我们要讨论一个更具有实际意义的问题——二元分类问题，我们会结识我们新的伙伴，激活函数。也敬请大家期待啦~
复制链接

扫一扫