线性代数 --- Gauss消元的部分主元法和完全主元法(补充)

松下J27

已于 2023-12-27 18:32:30 修改

阅读量1.9k

点赞数 1

分类专栏： Linear Algebra 文章标签：线性代数高斯消元 gauss 高斯消元法 LU分解

于 2022-12-22 18:09:28 首次发布

本文链接：https://blog.csdn.net/daduzimama/article/details/128405919

版权

Linear Algebra 专栏收录该内容

68 篇文章 60 订阅

订阅专栏

Gauss消元的部分主元法和完全主元法(补充)

本文主要是对下文的补充，而补充的主要内容就是如何直接(手动)写出部分主元法中的P矩阵和L矩阵：

线性代数 --- Gauss消元的部分主元法和完全主元法_松下J27的博客-CSDN博客_高斯消元的主元是什么Gauss消元的部分主元法和完全主元法https://blog.csdn.net/daduzimama/article/details/124797212

在我之前写的文章中，我留下了一个问题。那就是，在高斯消元的过程中，如果使用了行交换（或者列交换），怎么才能像不选主元法那样直接写出标准的下三角L矩阵呢？以及如何直接写出P矩阵，使得：PA=LU呢？后面，分别有两个热心的网友留言，并进行了答复。其中有一个网友的留言，我已经做了验证，并把他所说的算法补充到了原文中。后来，又有一位网友留言，同时推荐了一本书（如下图）：

这里面详细介绍了直接写出标准下三角矩阵L和置换矩阵P的办法。且，这本书里的方法和我前文中的方法不完全一样（可以说更好)，但也有相似之处。现在我就把书中的方法写出来，由于那本书中对矩阵的命名和我前文的命名有很大的不同，这里我依然沿用原书中的命名。

Part I: Lloyd N. Trefethen书中不选主元法的表示方式

这里，为了便于比较，我们依然沿用原来的例子：

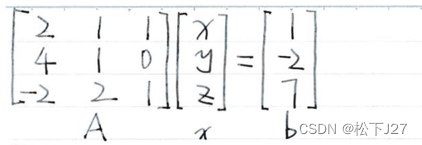
1，首先：就不选主元法而言，这本书并没有使用基本消元矩阵E来记录高斯消元的过程。而是用带有下标的矩阵 $\large L_{n}$ ，把第n列主元下所有元素的消元过程都放到一个矩阵中(也就是把一整列的消元过程用一个矩阵来记录)。下图为书中的示意图：

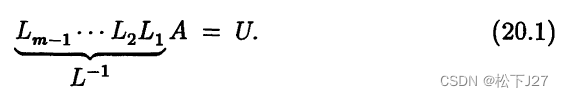
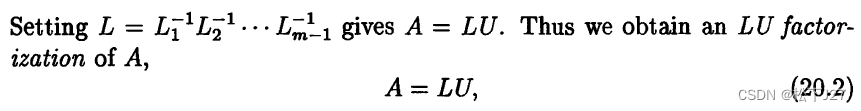
为了便于比较，我这里也把用消元矩阵 $E_{xy}$ 来表示的做法，用和书中类似的方式画下来了(红叉“x”表示值进行过更改):

也就是我原来的用法是用 $E_{nn-1}...E_{n2}...E_{42}E_{32}E_{n1}...E_{31}E_{21}A$ 来表示（或记录）消元过程的，而书中的作者是用 $L_{n-1}...L_{2}L_{1}A$ 来表示消元的过程。而且，从上面的列子，我们可以看出对于4x4的矩阵而言：

$\large E_{41}E_{31}E_{21}=L_{1}$

$\large E_{42}E_{32}=L_{2}$

$\large E_{43}=L_{3}$

2，此外:书中的L矩阵同样用到了基本消元矩阵E的两个性质。

2.1，若要计算基本消元矩阵 $E_{xy}$ 的逆，只需改变矩阵 $E_{xy}$ 中第x行，第y列元素的符号即可。

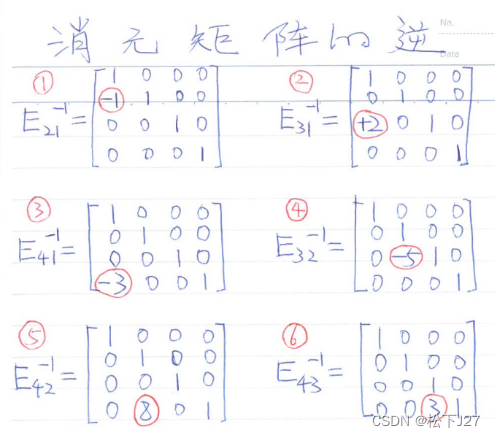
例如下面的六个消元矩阵和他们的逆矩阵（这不是本文起始处Ax=b所对应的消元矩阵）：

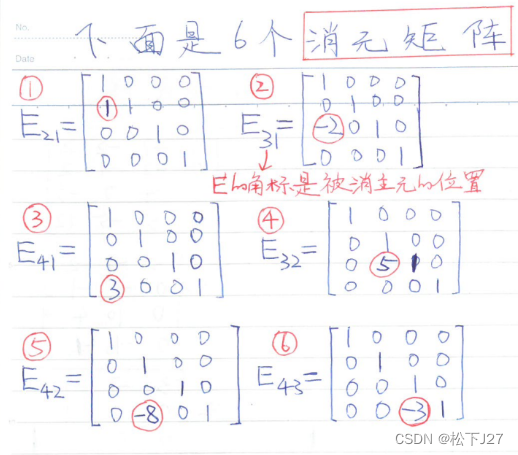
6个消元矩阵的逆（只需改变对应元素的符号即可）

2.2，要求多个的消元矩阵E的乘积，只需在单位矩阵I中，逐一填入 $E_{xy}$ 对应位置的值即可。(下面的例子中为多个消元矩阵的逆矩阵的乘积)

例如：

只不过，在这个作者的书中，他是以整列为单位操作的（即，以 $\large L_{n}$ 矩阵为单位处理的)，如下：

$L_{1}=\large E_{41}E_{31}E_{21}$

只需把三个消元矩阵 $E_{21}$ ， $E_{31}$ ， $E_{41}$ 中对应位置的值填入单位矩阵I中，就能得到矩阵 $\large L_{1}$ 。

同样，只要中间不涉及换行操作，按照同样的方法可写出 $\large L_{2}$ 和 $\large L_{3}$ 。

在他的书中，作者把上文中提到的消元矩阵 $E_{xy}$ 的两个特性称为两个LUCK“ two stroke of luck”。

Luck 1(20.4)：等同于消元矩阵E的第一条属性。即，逆矩阵只需改变对应元素的符号即可:

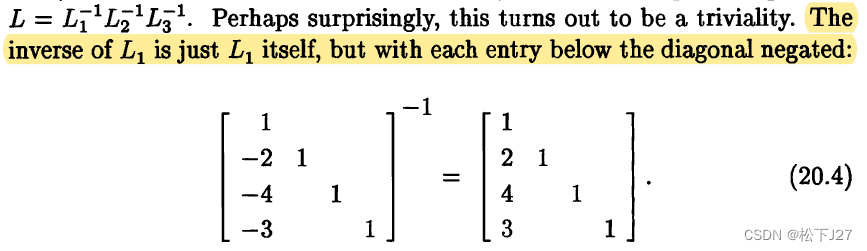
Luck 2(20.5)：等同于消元矩阵E的第二个属性。即，要求多个 $\large L_{n}$ 矩阵的乘积，只需把 $\large L_{n}$ 中的元素逐一填入单位矩阵I中对应的位置即可。

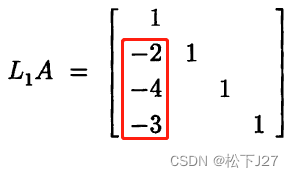
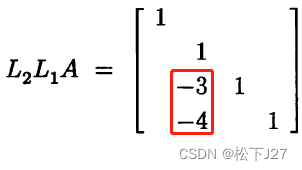
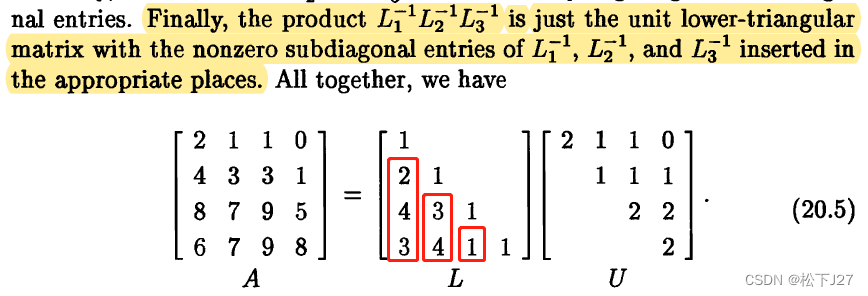
把L1，L2和L3中用红色方框框出来的元素(改变符号后。注意：L为多个L矩阵的逆矩阵的乘积)，逐一放在单位矩阵I中对应的位置，即可生成L矩阵。

$L={L_{1}}^{-1}{L_{2}}^{-1}{L_{3}}^{-1}$

下面我们用matlab来验证上述结论。

close all
clear all

%% 不分主元
L1=[1 0 0 0;-2 1 0 0;-4 0 1 0;-3 0 0 1]
L2=[1 0 0 0;0 1 0 0;0 -3 1 0;0 -4 0 1]
L3=[1 0 0 0;0 1 0 0;0 0 1 0;0 0 -1 1]

L1_inv=inv(L1)
L2_inv=inv(L2)
L3_inv=inv(L3)


L=L1_inv*L2_inv*L3_inv

不选主元法中的L1，L2，L3分别为：

L1，L2，L3的逆都是下三角矩阵，且根据这些逆可以直接写出L矩阵：

按照顺序依序填充单位矩阵，最终得到 $L={L_{1}}^{-1}{L_{2}}^{-1}{L_{3}}^{-1}$

按照作者Lloyd N. Trefethen的做法，我也把用多个消元矩阵 $E_{xy}$ 相乘的表示方式和用文中多个 $\large L_{n}$ 矩阵相乘的表示方式做了一个类比。

多个基本消元矩阵E的逆相乘得到的L矩阵：

多个 Ln矩阵的逆相乘得到的L矩阵：

Part II: Lloyd书中部分主元法的表示方式

不选主元法，并不是本文的重点。下面我们看看在他的书中，如果遇到了行交换的问题，他是怎么直接写出L矩阵的。

1，首先，他在这里也是用P表示置换矩阵。

2，和用消元矩阵E+置换矩阵P的表示方式一样，他也是按照从A到U的消元过程，按照消元的顺序，把整个消元过程用若干个置换矩阵P和消元矩阵L的乘积表示。（唯一不同的就是在我的方法中用的是E矩阵记录消元过程，而在他的方法中用的是L矩阵）

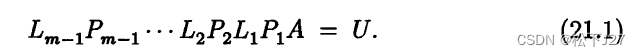
我们先看看书中的一个例子，以便更好的理解他的做法，尤其要注意他的L'矩阵：

（下图中的L1应为L2）

最终，按照从A到U的消元顺序得到：

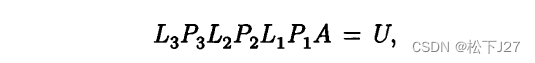
注意：这里L3P3L2P2L1P1逐一相乘后的结果和前面不选主元法的例子中得到的L3L2L1可不一样。由于置换矩阵P的存在，他得到的不是一个标准的下三角矩阵，但后者（L3L2L1）是，且后者的逆也是。

同样，我们用matlab来验证这一结论：

%% 部分主元
P1=[0 0 1 0;0 1 0 0;1 0 0 0;0 0 0 1]
L1=[1 0 0 0;-1/2 1 0 0;-1/4 0 1 0;-3/4 0 0 1]
P2=[1 0 0 0;0 0 0 1;0 0 1 0;0 1 0 0]
L2=[1 0 0 0;0 1 0 0;0 3/7 1 0; 0 2/7 0 1]
P3=[1 0 0 0;0 1 0 0;0 0 0 1;0 0 1 0]
L3=[1 0 0 0;0 1 0 0;0 0 1 0;0 0 -1/3 1]

P1_inv=inv(P1)
L1_inv=inv(L1)
P2_inv=inv(P2)
L2_inv=inv(L2)
P3_inv=inv(P3)
L3_inv=inv(L3)

L=P1_inv*L1_inv*P2_inv*L2_inv*P3_inv*L3_inv

A=[2 1 1 0;4 3 3 1;8 7 9 5;6 7 9 8]

[l u]=lu(A)

部分主元法中的P1,L1,P2,L2,P3,L3分别为：

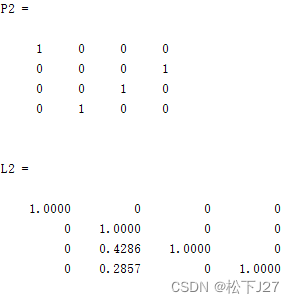
他们的逆为：

注意：因为P矩阵的引入，这些矩阵的逆矩阵的乘积L=P1'L1'P2'L2'P3'L3'并不是一个标准的下三角矩阵。

更重要的是，在有P矩阵的情况下，你很难直接写出标准的下三角矩阵L。一般情况下，算到这里就结束了，且能得到和matlab自带函数相同的结果：

但，这本书的作者提到了一个可以直接写出标准下三角矩阵L的办法，并称之为第三个LUCK：

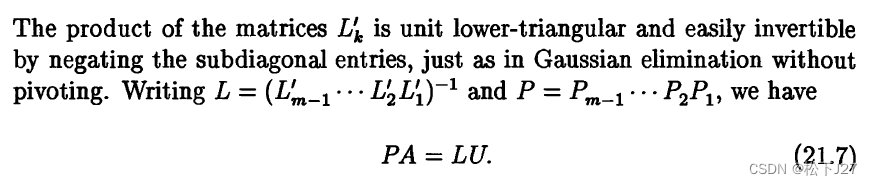
用他的话说就是，我们最终想得到的PA=LU中的P和L，他们分别由：

和

这两个公式给出。

举个例子吧，如果是用部分主元法对一个4x4的矩阵消元，则我们所需要的L1',L2'和L3'分别是：

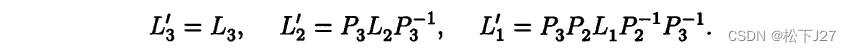
而最终的L应该等于：

$\large L=(L_{3}^{'}L_{2}^{'}L_{1}^{'})^{-1}={L_{1}^{'}}^{-1}{L_{2}^{'}}^{-1}{L_{3}^{'}}^{-1}$

分别代入上面的L1',L2'和L3'得到（置换矩阵的逆等于他自己）：

$\large L=(P^{3}P^{2}L^{1}{P^{2}}^{-1}{P^{3}}^{-1})^{-1}(P^{3}L^{2}{P^{3}}^{-1})^{-1}(L^{3})^{-1}=(P^{3}P^{2}L^{1}{P^{2}}{P^{3}})^{-1}(P^{3}L^{2}{P^{3}})^{-1}(L^{3})^{-1}$

我们按照书中的说法做一遍，看看最终的结果：

用matlab来验证上述过程：

%% 第三个LUCK
L3p=L3
L2p=P3*L2*P3
L1p=P3*P2*L1*P2*P3

L3p_inv=inv(L3p)
L2p_inv=inv(L2p)
L1p_inv=inv(L1p)

L_standard=L1p_inv*L2p_inv*L3p_inv

1,先求L1',L2'和L3'

2,求出他们的逆

3，求出标准下三角矩阵L

最后，我用他的这个方法来计算本文最开始的那个例子，有兴趣的读者可以和我原文中用消元矩阵E+置换矩阵P的算法算法做个对比：（尤其是要注意PnLn左乘和LnPn右乘的区别，以及右乘对最终L矩阵的影响，我想这就是作者所说的第三个Luck吧）

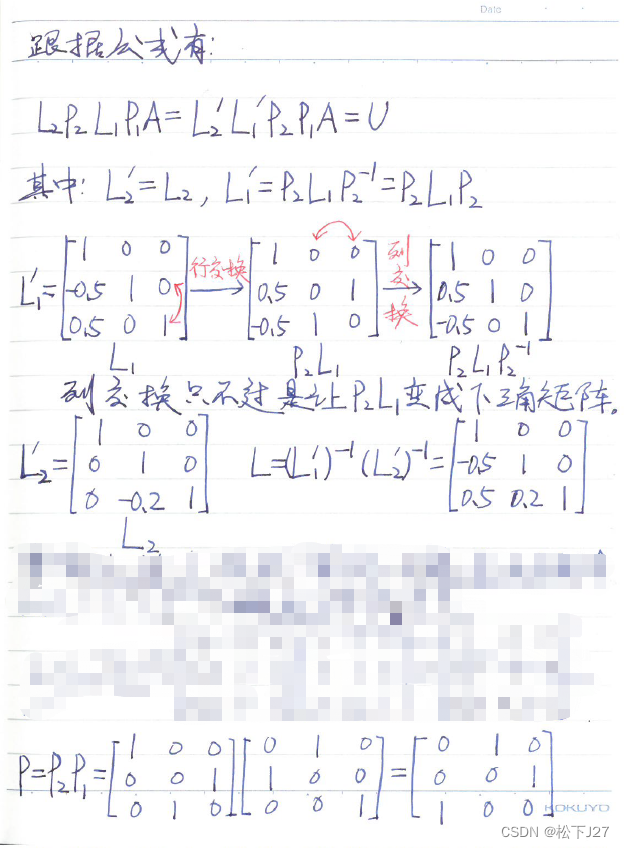
这里我们要注意两点：

1，在计算Ln'矩阵时要注意：Ln'等于若干个置换矩阵P左乘Ln和若干置换矩阵P的逆右乘Ln。

当我们自己手算时(也许包括编程时)，如果注意到Ln后面所乘的一系列的置换矩阵P的逆，都只是为了把前面PPPP...PLn的结果变成下三角矩阵而已的话。

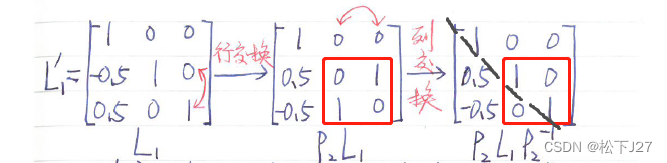
且，我们在写L矩阵时也只是用到了Ln'中的第n列主元下面的值(要改变符号)，完全不需要考虑他究竟是不是标准的下三角矩阵，也就是说大可不需要Ln后面的一系列的列交换操作，依然也能写出L矩阵。

这样一来我们在计算Ln'时，可以选择一种取巧的办法，不去管Ln后面的P，只需把PPPP...PLn乘起来即可。

2，私以为，他的这种表示方法，有一个地方可以改进，那就是把P1，P2。。。的命名方式改成P14(交换14行),P23(交换23行)可能会更好，这样更直观一些。但，似乎又不利于计算Ln时的排序。。。

（全文完）

作者 --- 松下J27

古诗词赏析：

《破阵子·为陈同甫赋壮词以寄》

---辛弃疾

醉里挑灯看剑，梦回吹角连营。八百里分麾下炙，五十弦翻塞外声，沙场秋点兵。
马作的卢飞快，弓如霹雳弦惊。了却君王天下事，赢得生前身后名。可怜白发生！

参考文献（鸣谢）：

《Numerical Linear Algebra》---Lloyd N. Trefethen, David Bau

（配图与本文无关）

松下J27

关注

1
点赞
踩
7

收藏

觉得还不错? 一键收藏
打赏
0
评论
线性代数 --- Gauss消元的部分主元法和完全主元法(补充)

直接写出部分主元高斯消元法中的L矩阵和P矩阵的方法。
复制链接

扫一扫

专栏目录