偏导数(是一个标量)
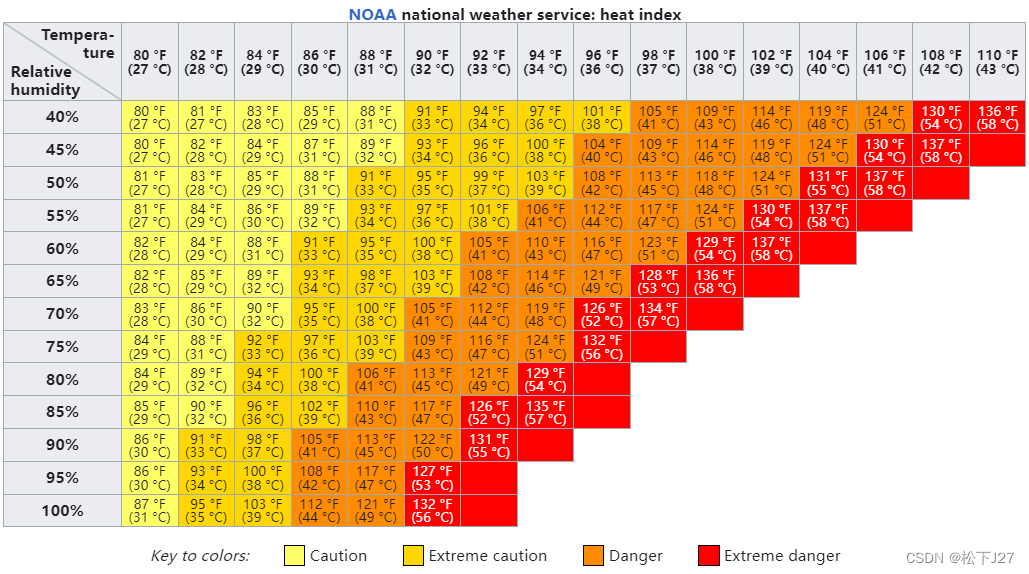
在非常炎热的夏天,如果再加上非常潮湿天气,人们就会觉得更热。或者说,实际体感感受到的温度会比天气预报或者温度计上所显示的温度热的多。这是因为人体通过排汗来达到降温的目的,在这个过程里汗液中的水分得以蒸发并且从人体带走热量。但是当相对湿度较高时,水分的蒸发率就会降低。这意味着从身体中带走热量的过程变得缓慢,针对这一现象,美国的国家气象服务局给出了一个叫heat index(酷热指数)的东西,用于描述温度temperature和湿度humidity综合效应。
heat index I表示的是当实际温度T为某一定值时,随着相对湿度H的变化,体感温度的变化。比如说,当温度为30摄氏度时,湿度为40%时,体感温度是29度,但当相对湿度升高到80%时,体感温度就会上升到38度。
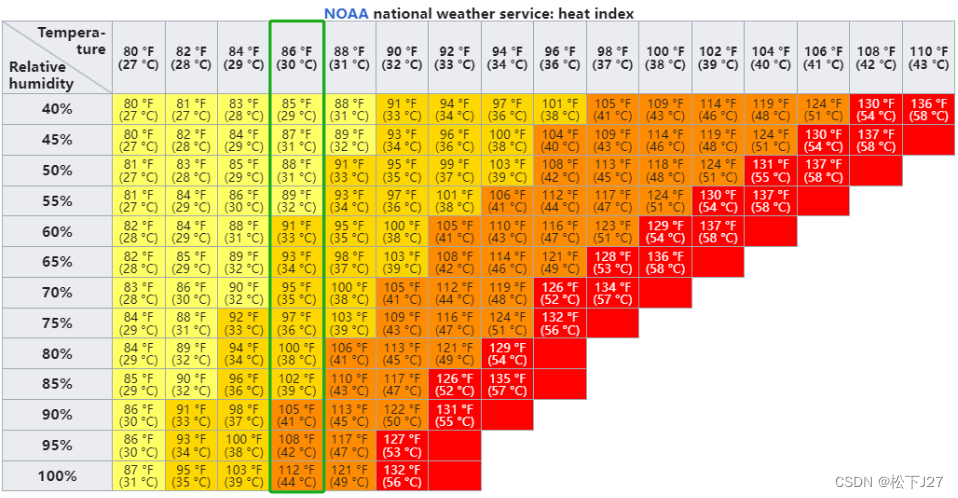
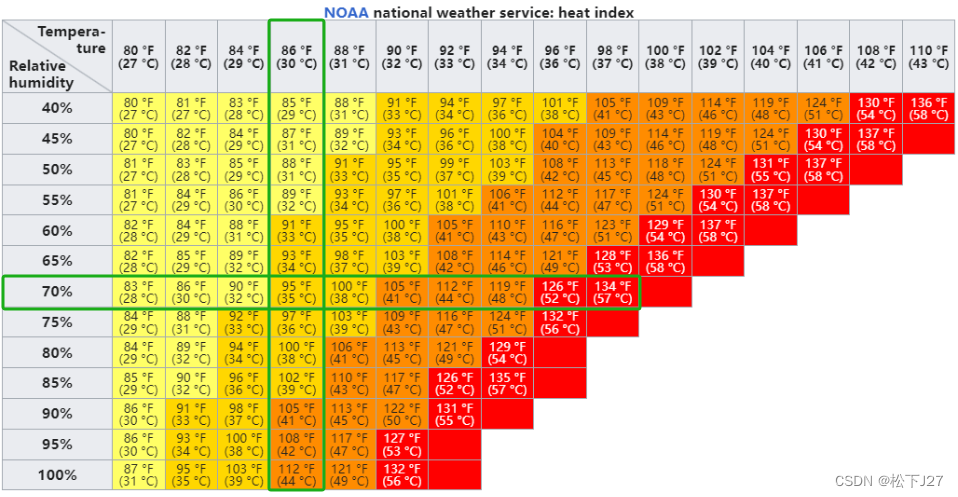
同样的, 如果把相对湿度稳定到70%,可以看到当实际温度是27度时,体感温度和实际温度还差不多,但当实际温度上升到28度后,体感温度就开始变得比实际温度高了(30度)。
这就是说,上述表格中的关系可以转换为一个数学模型,即,I是T和H的函数:
当我们固定一个变量不变去观察函数值随着另一个变量的变化而变化时,正如我们上面的做法那样。实际上这就是偏导的实际含义!
下图是酷热指数表中所截取的一部分:
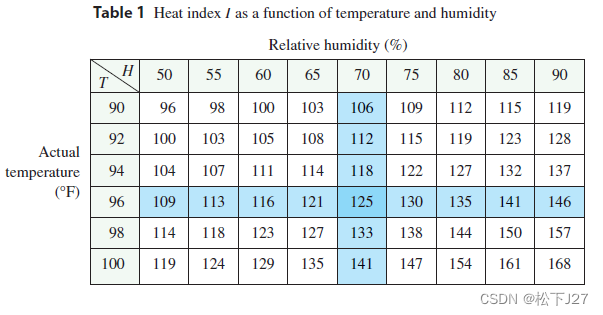
我们用函数g(T)=f(T,70)表示相对湿度稳定在70%时,体感温度(也就是酷热指数)随实际温度的变化程度。根据导数的定义我们可以求出,函数g(T)在T=96时的瞬时变化率。
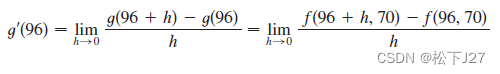
分别用T等于94,96和98时的数值去估算瞬时变化率,即,函数关于T的导数在T=96这一点处的导数值。
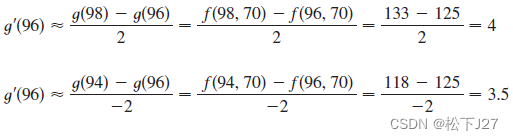
如果我们把上面的酷热函数I=f(T,H),用更一般的二元函数z=f(x,y)来表示,并且固定y为一常数b,使原函数变成了一个只随一个自变量而变化的新函数g(x)=f(x,b)。然后再求函数g(x)在x=a处的导数的这一计算过程,我们称之为,对f求x在(a,b)处的偏导。

代入求导的极限公式:
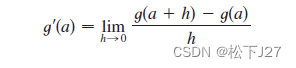
有:
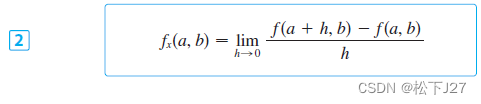
同样的,如果用G(H)=f(96,H)来表示当实际温度为华氏96度时,体感温度关于相对湿度的函数。求H=70%时的导数值G'(70):
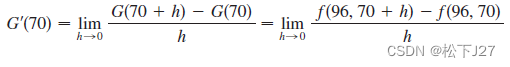
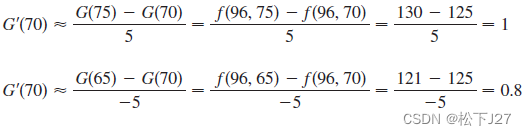
套用一般二元函数表达式,这是对y求点(a,b)处的偏导:
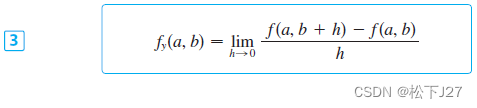
最终得到对于二元函数的偏导数的一般表达式:

下面是偏导数的常见表达式,他们所表示的都是同一个东西,只是写法不同:

这是偏导数的求法:

例子:

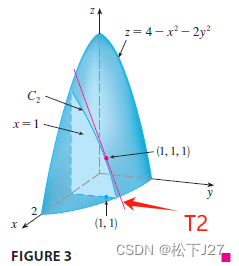
偏导数的几何解释:
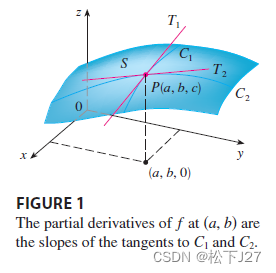
上图中曲面S由二元函数z=f(x,y)给出,若f(a,b)=c,则点P(a,b,c)在曲面S上。令y=b,得到曲线C1及其对应的函数g(x)=f(x,b)。求g(x)在x=a处的偏导g'(a),得到曲线C1所对应的切线T1在点(a,b,c)处的斜率。同理,令x=a得到曲线C2,G(y)=f(a,y)。与之对应的切线T2在点(a,b,c)处的斜率就是G(y)在y=b处的偏导数G'(b)。
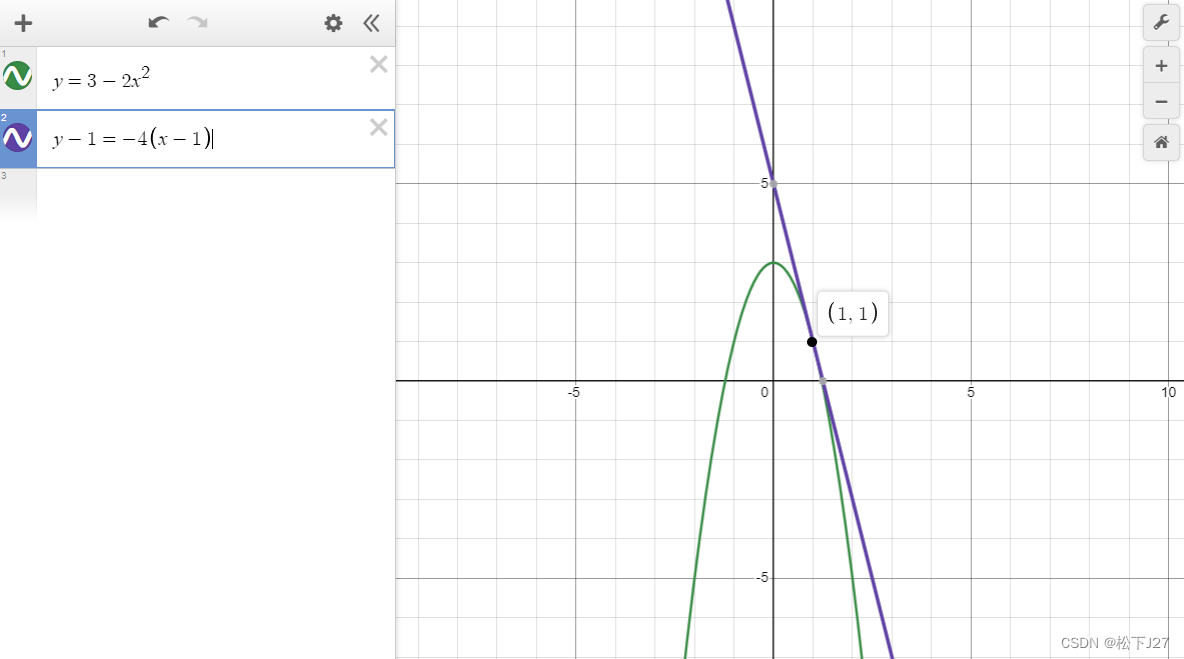
例子:
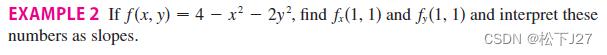
求f关于x的偏导。
当y=1时:
得到曲线C1的函数。
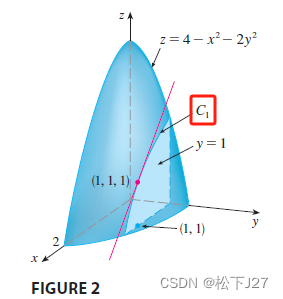
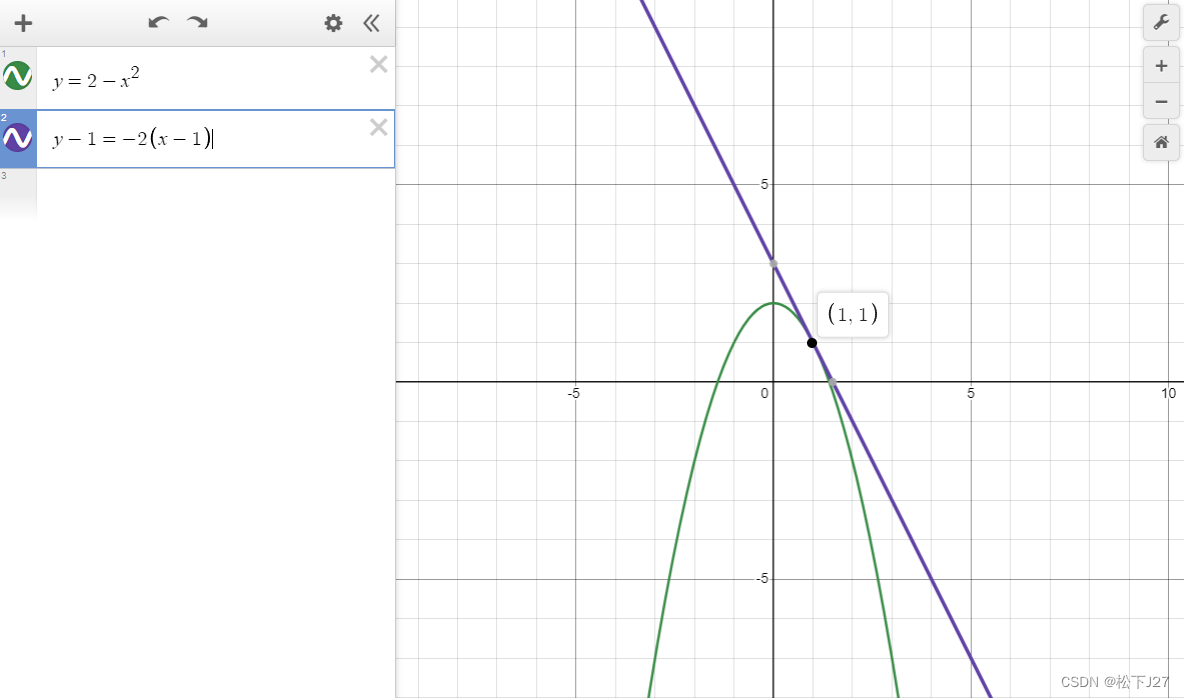
求f(x,1)关于x的导数:
代入x=1,得到,函数在x=1处的切线的斜率:
把斜率代入点斜式方程,得到,函数在x=1处的切线T1:
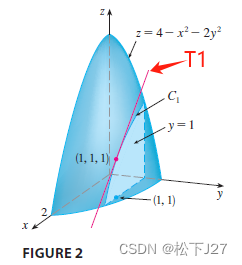
求f关于y的偏导。
令x=1,得到函数:
这就是曲线C2。
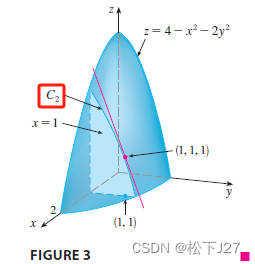
求f(1,y)关于y的导数:
代入y=1,得到,函数在y=1处的切线的斜率:
把斜率代入点斜式方程,得到,函数在y=1处的切线T2:
(全文完)
--- 作者,松下J27
参考文献:
1,https://zh.wikipedia.org/wiki/%E9%85%B7%E7%83%AD%E6%8C%87%E6%95%B0
3,https://en.wikipedia.org/wiki/Heat_index
4,Calculus --- James Stewart,page 952 chapter 14

(配图与本文无关)
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27























 926
926

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










