从头学pytorch(四)　softmax回归实现

最新推荐文章于 2024-08-16 13:19:57 发布

山与海丫

最新推荐文章于 2024-08-16 13:19:57 发布

阅读量1.3k

点赞数 1

本文链接：https://blog.csdn.net/dengyu810/article/details/103718067

版权

FashionMNIST数据集共70000个样本,60000个train,10000个test．共计10种类别.
www.wityx.com

通过如下方式下载．

mnist_train = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST', 
                                                train=True, download=True, 
                                                transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST', 
                                               train=False, download=True, 
                                               transform=transforms.ToTensor())

softmax从零实现

数据加载
初始化模型参数
模型定义
损失函数定义
优化器定义
训练

数据加载

import torch
import torchvision
import torchvision.transforms as transforms

mnist_train = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST',
                                                train=True, download=True,
                                                transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST',
                                               train=False, download=True,
                                               transform=transforms.ToTensor())
batch_size = 256
num_workers = 4  # 多进程同时读取
train_iter = torch.utils.data.DataLoader(
    mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(
    mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)

初始化模型参数

num_inputs = 784  # 图像是28 X 28的图像,共784个特征
num_outputs = 10

W = torch.tensor(np.random.normal(
    0, 0.01, (num_inputs, num_outputs)), dtype=torch.float)
b = torch.zeros(num_outputs, dtype=torch.float)

W.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)

模型定义

记忆要点:沿着dim方向.行为维度0,列为维度１. 沿着列的方向相加,即对每一行的元素相加.

def softmax(X):  # X.shape=[样本数,类别数]
    Ｘ_exp = X.exp()
    partion = X_exp.sum(dim=1, keepdim=True)  # 沿着列方向求和,即对每一行求和
    #print(partion.shape)
    return X_exp/partion  # 广播机制,partion被扩展成与Ｘ_exp同shape的,对应位置元素做除法

def net(X):
    # 通过`view`函数将每张原始图像改成长度为`num_inputs`的向量
    return softmax(torch.mm(X.view(-1, num_inputs), W) + b)

损失函数定义

假设训练数据集的样本数为\(n\)，交叉熵损失函数定义为
\[\ell(\boldsymbol{\Theta}) = \frac{1}{n} \sum_{i=1}^n H\left(\boldsymbol y^{(i)}, \boldsymbol {\hat y}^{(i)}\right ),\]

其中\(\boldsymbol{\Theta}\)代表模型参数。同样地，如果每个样本只有一个标签，那么交叉熵损失可以简写成\(\ell(\boldsymbol{\Theta}) = -(1/n) \sum_{i=1}^n \log \hat y_{y^{(i)}}^{(i)}\)。

def cross_entropy(y_hat, y):
    y_hat_prob = y_hat.gather(1, y.view(-1, 1))  # ,沿着列方向,即选取出每一行下标为y的元素
    return -torch.log(y_hat_prob)

https://pytorch.org/docs/stable/torch.html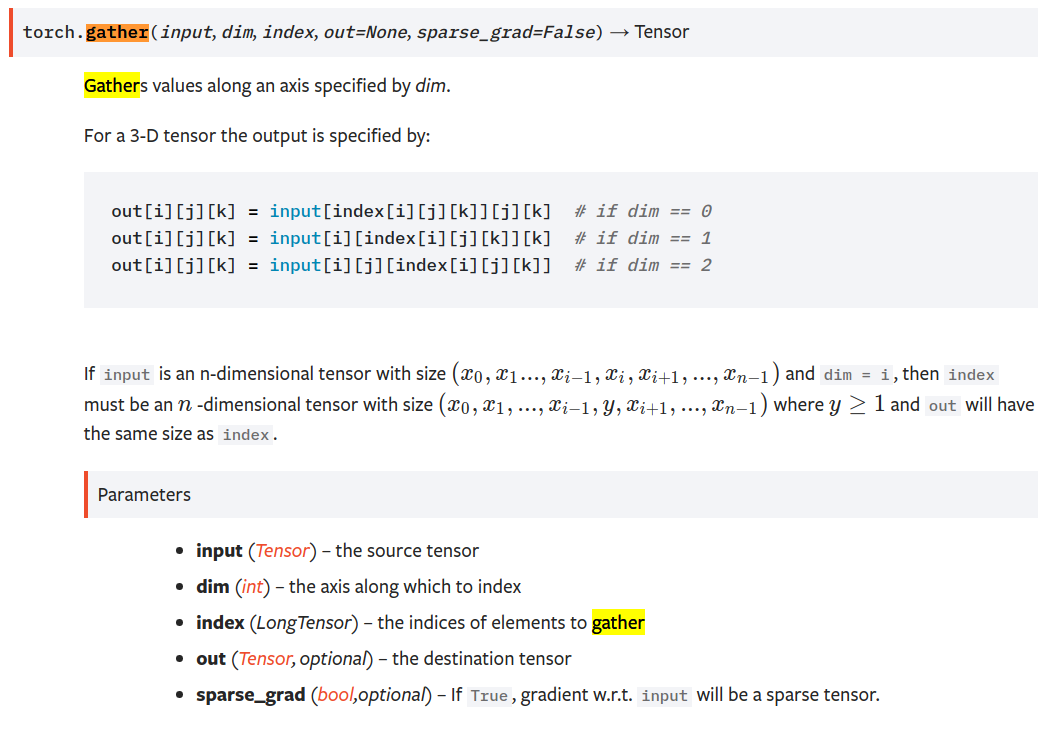
www.wityx.com
gather()沿着维度dim,选取索引为index的元素

优化算法定义

def sgd(params, lr, batch_size):
    for param in params:
        param.data -= lr * param.grad / batch_size  # 注意这里更改param时用的param.data

准确度评估函数

def evaluate_accuracy(data_iter, net):
    acc_sum, n = 0.0, 0
    for X, y in data_iter:
        acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
        n += y.shape[0]
    return acc_sum / n

训练

读入batch_size个样本
前向传播,计算预测值
与真值相比,计算loss
反向传播,计算梯度
更新各个参数
如此循环往复.

num_epochs, lr = 5, 0.1
def train():
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter:
            #print(X.shape,y.shape)
            y_hat = net(X)
            l = cross_entropy(y_hat, y).sum()  # 求loss
            l.backward()  # 反向传播,计算梯度
            sgd([W, b], lr, batch_size)  # 根据梯度,更新参数

            Ｗ.grad.data.zero_()  # 清空梯度
            b.grad.data.zero_()

            train_l_sum += l.item()
            train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
            n += y.shape[0]
        test_acc = evaluate_accuracy(test_iter, net)
        print('epoch %d, loss %.4f, train_acc %.3f，test_acc %.3f'
              % (epoch + 1, train_l_sum / n, train_acc_sum/n, test_acc))

train()

输出如下：

epoch 1, loss 0.7848, train_acc 0.748，test_acc 0.793
epoch 2, loss 0.5704, train_acc 0.813，test_acc 0.811
epoch 3, loss 0.5249, train_acc 0.825，test_acc 0.821
epoch 4, loss 0.5011, train_acc 0.832，test_acc 0.821
epoch 5, loss 0.4861, train_acc 0.837，test_acc 0.829

-------

softmax的简洁实现

数据加载
模型定义及初始化模型参数
损失函数定义
优化器定义
训练

数据读取

import torch
from torch import nn
from torch.nn import init
import numpy as np
import sys
import torchvision
import torchvision.transforms as transforms

mnist_train = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST',
                                                train=True, download=True,
                                                transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST',
                                               train=False, download=True,
                                               transform=transforms.ToTensor())
batch_size = 256
num_workers = 4  # 多进程同时读取
train_iter = torch.utils.data.DataLoader(
    mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(
    mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)

模型定义及模型参数初始化

num_inputs = 784  # 图像是28 X 28的图像,共784个特征
num_outputs = 10

class LinearNet(nn.Module):
    def __init__(self,num_inputs,num_outputs):
        super(LinearNet,self).__init__()
        self.linear = nn.Linear(num_inputs,num_outputs)
    
    def forward(self,x):  #x.shape=(batch,1,28,28)
        return self.linear(x.view(x.shape[0],-1))　#输入shape应该是[,784]

net = LinearNet(num_inputs,num_outputs)

torch.nn.init.normal_(net.linear.weight,mean=0,std=0.01)
torch.nn.init.constant_(net.linear.bias,val=0)

没有什么要特别注意的,注意一点,由于self.linear的input size为[,784]，所以要对x做一次变形x.view(x.shape[0],-1)

损失函数定义

torch里的这个损失函数是包括了softmax计算概率和交叉熵计算的．

loss = nn.CrossEntropyLoss()

优化器定义

optimizer = torch.optim.SGD(net.parameters(),lr=0.01)

训练

精度评测函数

def evaluate_accuracy(data_iter, net):
    acc_sum, n = 0.0, 0
    for X, y in data_iter:
        acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
        n += y.shape[0]
    return acc_sum / n

训练

读入batch_size个样本
前向传播,计算预测值
与真值相比,计算loss
反向传播,计算梯度
更新各个参数
如此循环往复.

num_epochs = 5
def train():
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X,y in train_iter:
            y_hat=net(X)   #前向传播
            l = loss(y_hat,y).sum()#计算loss
            l.backward()#反向传播

            optimizer.step()#参数更新
            optimizer.zero_grad()#清空梯度

            train_l_sum += l.item()
            train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
            n += y.shape[0]

        test_acc = evaluate_accuracy(test_iter, net)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
                % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))

train()

输出

epoch 1, loss 0.0054, train acc 0.638, test acc 0.681
epoch 2, loss 0.0036, train acc 0.716, test acc 0.724
epoch 3, loss 0.0031, train acc 0.749, test acc 0.745
epoch 4, loss 0.0029, train acc 0.767, test acc 0.759
epoch 5, loss 0.0028, train acc 0.780, test acc 0.770