《鞋匠的AI之旅》- 1. 缘起 & 2. 新生【简析人工神经网络的原理】

1.缘起

【内含公式，建议PC端浏览器阅读】

鞋匠的工作是擦鞋，拂去过往者鞋上的尘埃是他的生活日常。鞋匠常说，鞋如心镜照见每个浮念，时时勤拂拭，不使惹尘埃，而熙熙攘攘的大街上很少有人会停下脚步，来到路边鞋匠的小摊。

鞋匠正擦着鞋，西装革履的顾客对着手里的电话说个不停,“GPT，Transformer，填空题，选择题，大模型，…”，情绪飘扬，指点着领域的未来。原本淅淅沥沥的小雨没有带来一丝凉意。这让鞋匠的思绪回到了那个激情燃烧的岁月，那时股市是头猛牛，昂首阔步四处冲击，遍地黄金，也有一个顾客电话里谈论着股市的涨跌，指点着这片股市江山。鞋匠累了，他娴熟的擦完眼前的这双鞋，早早地收工了。

窗外起风了，斜风缠着细雨，迷了人眼。鞋匠提笔写下了自己的初心，好在初心还在，心里平静了许多。他带上了自己心爱的眼镜，尝试着看清事物的本质。看着自己刚刚写下的这段话，鞋匠闭上眼，暂且忘却了身边的浮华，仔细地体会着。他悟到，有些人读完这段文字会觉得唯美，有些可能觉得幽默，有些可能体会到些许幽怨，有些则觉得带有些许讽刺。而鞋匠深知自己真正怎么想的、想表达什么，没有人可以百分之百体会得到。这就是语言。它那么简单，不需要做出什么努力就都能体会的到，张嘴可得。它又是这么的复杂，每个人都有独有的处理和理解，难以琢磨。鞋匠试图躲闪着什么，但眼前有一个问题始终挥之不去：今天那个顾客谈论的大模型是什么，它又是怎么来处理并体会这一切的呢？

如果人工智能（AI）是树林，那大模型已长成了一棵参天大树。它枝繁叶茂，叶子遮盖了众多的枝干。鞋匠怀着敬畏之心观察着这棵大树，多么希望通过观察外表的众多树叶来了解它，掌握它，然而它是那么复杂壮阔的智能奇迹，繁茂的枝叶遮盖了各级枝干的脉络。如果自己能够穿越时间那该多好，这样就可以看到这棵大树最初的模样，那棵战战兢兢的嫩苗，等待着巨大的算力来滋养！

2.新生

鞋匠思索着，仿佛看到了远古时代的那棵幼苗。那是一个简单的2维世界，一个维度是时间，另一个维度是高低位置，所有人都和谐地生活在这个2维的平面里，而鞋匠是这个2维世界的科学家。在那里，每个人的人生轨迹只是简单的随着时间的流逝而高低变化着，当下在二维平面的这个位置，下一时刻在那个位置，但轨迹是连续的。从数学上看，一个人的人生轨迹像极了一条2维平面的曲线，y=f(t)，这里只有一个横轴的自变量时间t和一个纵轴的因变量高低位置y。如图0所示，那是鞋匠的人生轨迹。在过去的时间t1到t5鞋匠有着清晰的轨迹，他经历了人生的巅峰，也曾跌落谷底，但谁也不知道在未来的时间，如t6，t7，会如何发展，他可能又一次扶摇直上，如绿色虚线所示，也可能再次跌下神坛，如红色的虚线所示。所以鞋匠很想预测自己生活的未来，即他想知道未来下一个时间点自己在哪，不用等到未来的时间点到来时才知道自己具体的位置。从数学上看，可以说是预测下一个时刻t对应的y的值。这样他就可以完全掌控自己的人生了，就像今天可以看到明天的股市一样，一切都将变得无比的美妙。

图0，鞋匠的人生轨迹

复杂是简单的叠加

鞋匠开始了自己的研究，他先在纸上画下了两个可能的人生轨迹，如图1，图2所示。

图1，轨迹1

图2，轨迹2

可以看到这两个轨迹的变化都比较单一，按照各自的变化模式周期性地重复着。从信息学上看，鞋匠称这两个都是单一频率的信号。接下来鞋匠把这两个轨迹叠加在了一起，形成了如图3所示的轨迹3。

图3，轨迹3

轨迹3已经看不出原来周期性的变化模式了，但它是两个单一周期性变化的轨迹叠加而成的。鞋匠灵光乍现，是不是复杂的轨迹都可以分解为单一的轨迹的叠加呢？鞋匠觉得自己是对的，后来他在傅里叶的论文里找到了依据：满足一定条件的周期性连续信号，可以被唯一且精确地表示为无穷级数的形式，该级数由一系列特定频率、不同强度和不同相位的正弦函数与余弦函数组成，这个无穷级数被称为傅里叶级数。他不懂傅里叶在说什么，但鞋匠觉得这是他简化问题方法的一种印证，即“复杂”是“简单”的叠加。在他的2维世界里，复杂的轨迹应该都可以简化为众多单一周期性变化轨迹的叠加。

鞋匠很满意自己脑子里闪过的那道灵光。接下来怎么选择“简单”的曲线呢？鞋匠想还是得从现实入手。现实当中，经常要处理的问题是这样的：

• 灰与白：这一类问题一般会要求根据一定的信息来判断对与错，判断它是不是某个或者某类东西，是这类东西的可能性,衡量某种程度等等。如果对这一类问题进行量化，量化值一般会落在0到1之间的某个值上。如果这个值是0，则判为“不是”，如果是1则判为“是”，介于0和1之间，就是对这个判断的置信度，比如0.9则表示有90%的信心说它是对的。于是，鞋匠在纸上画了图4的一个曲线来表示这一单一的“简单”曲线。
• 左与右：在上面的灰与白的问题中，不会出现小于0的值（纵轴的取值大于0）。但有一类问题是需要考虑负值来表示相反的方向，比如，向左转30度，和向右转30度，都是30度，只用大于0的30这个数值就无法表示向左还是向右了。于是鞋匠把上面的曲线下移到了负数区间，用负号来代表相反的方向，如图5。
• 断与舍：有些时候，负数是没有意义的，比如股市，它不会出现面值为负数的股票，而大于0的真实的面值一丝一毫也不能少。于是，鞋匠把小于0的情况都舍弃掉，当作0来处理，而大于0是保持不变的，得到了图6所示的“简单”曲线。
• 选与决：有时候一个人会面临多个选项，而又必须对选哪个做出决断。假设你的面前有三条路，而生活还要继续，你必须选择一条路走下去，怎么选呢？你可能希望有人帮你分析下，每条路给出了一个概率，有20%的概率选路1，30%的概率选路2，50%的概率选路3。这种情况下是你总是要选择一条路，而面前只有3条路，所以选择每条的路的概率加起来是100%，即你总要选择一条走下去。如果把这三个概率值放到一起来表示，可以用有3个元素的1组数来表示，即(0.2, 0.3, 0.5)。这条“曲线”看起来不再是条曲线，它是离散的，但它是有意义的。鞋匠还是试图把它形象化的展示出来了，如图7（后来被证明这是在概率论中经常用到的函数）。

为什么是这样的一些曲线呢？鞋匠心里也没底，至少它们是鞋匠喜欢的模样。鞋匠认为这些是问题答案的基本单元，把这些简单的基本单元叠加在一起，就是要找的问题答案，至于对与错就交给时间吧。

图4，Sigmoid函数

图5，Tanh函数

图6，ReLU函数

（p1，p2，p3，…,pn），其中0≤ pn ≤1 , p1 + p2 + p3 + … + pn = 1

图7，Softmax函数

第一个神经元

这些简单的曲线是没有灵魂的，鞋匠不想整天面对的是一堆的曲线，得为它们找个宿主，体现其“简单”的生命力，这样才能通过叠加形成一个有机体。这个有机体可以自我进化，形成自己的模式，找到“复杂”问题的答案，即在鞋匠的2维世界里模拟他那条复杂的生活轨迹，预测未来的走向。这就是鞋匠要寻找的“智能”，人工的智能！

说到有机体，鞋匠想到了生物学课堂上的内容。老师说有机体是由简单的细胞组成的，包括你的大脑。大脑是一个人智慧的中心，由众多的神经元细胞组成。每个神经元通过树突来接收一个或者多个神经元的信号，经过神经元的处理后再通过轴突把处理过的信号发送到下一个或者多个神经元。在单个神经元层面一切都是那么的简单，当大约1000亿个神经元高度复杂地连接在一起的时候，经过不断学习，就产生了智慧，但科学家在大脑里并没有发现一个“我”或者独立“意识”的存在，这真得很神奇。鞋匠也不知道这一切是怎么发生的，但他觉得这和“复杂是简单的叠加”有关。鞋匠重复着这些想法，“复杂是简单的叠加”，“复杂曲线是简单曲线的叠加”，“智慧的大脑是简单神经元的叠加”。等等！简单曲线和神经元貌似可以结合起来。“赋予简单曲线灵魂的是神经元”鞋匠心里有了答案！

鞋匠重新审视着他画出的简单曲线，在数学上他们都以函数的形式表示，如图4的Sigmoid函数，图5的Tanh函数，图6的ReLU函数，图7的Softmax函数。怎么把这些函数和神经元结合在一起呢？鞋匠在纸上画了一个圈，并用左侧的连线表示输入，右侧的连线表示输出，它和一个真正的大脑神经元的机理类似，接收输入，发出处理结果，如图8。将某个函数与一个神经元结合在一起就是将这个函数作用于一个神经元上，这意味着：这个神经元把接收到的信号量，输入给这个函数，并将函数的运算结果作为输出信号量发送出去。如果把神经元想象成一个载体，那激活它的就是作用在它上面的“简单”曲线的函数。鞋匠把这类函数称之为激活函数。

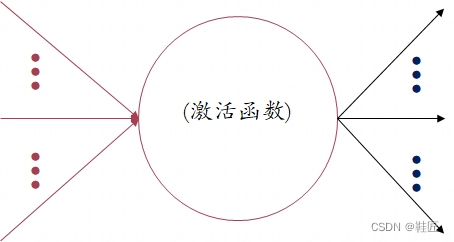
图8，一个神经元

现在回到鞋匠2维世界的生活轨迹上，一个神经元输入就是某个时间量t（即某个时间点），输出就是作用在这个神经元上对应的激活函数的运算结果。每一个神经元的运算结果对于同一个输入量来说都是一样的，那么把众多一样的神经元的运算结果加在一起并不能形成复杂的曲线，而只是增加了原来简单曲线的输出幅度，改变不了原函数的周期性变化模式。正如前面曲线叠加的例子，图1和图2的曲线都是简单的周期性变化的曲线，但其周期变化的模式不一样，经过叠加才形成了图3的复杂曲线。如果两个图1的曲线加在一起，曲线的形状还是类似图1的曲线，只是上下震动的幅度变大了。这是个问题，需要解决！

他翻开了傅里叶的那篇论文，“傅里叶级数由一系列特定频率、不同强度和不同相位的正弦函数与余弦函数组成”。“频率”、“强度”、“相位”，这三个词在他眼前最为活跃。一个复杂信号之所以可以被精确的表示出来，和这三个性质有关，其中频率对应着周期性，强度对应着上下震动幅度，相位对应着起始位置。鞋匠的简单曲线有着与周期对应的单一性，但没有与强度和相位对应的调整。这些简单曲线在强度上的调整，就相当于对原简单曲线上每个点的y值的放大和缩小，如下：

y = a1 ×  Sigmoid(t)；

y = a2 ×  Tanh(t)；

y = a3 ×  ReLU(t)；

y = a4 ×  Softmax(t)

图9，上下幅度调整

这里a1，a2，a3，a4 都是常数，即不随时间t变化的数，它们对应不同曲线上下幅度的放大和缩小。a的值大于1，就是对原曲线上下幅度的放大，小于1就是对原曲线上下幅度的缩小，等于1就是原曲线保持不变。鞋匠把a这类数称之为权重。除了上下幅度的调整，整体曲线还可以左右移动的调整，这就是傅里叶级数里不同相位给予鞋匠的启示。一个曲线的整体左移一小段“距离”，相当于自变量加上这段“距离”对应的量，而整体右移，就相当于自变量上减去对应的量。有意思的是加和减在数学上是可以相互转化的，比如加上一个负数，将相当于减去这个数所对应的正数，即t + (-7) = t - 7。所以在上下调整的基础上，整体曲线的左右调整就可以都用加法形式来表示了：

y = a1 ×  Sigmoid(t + b1)；

y = a2 ×  Tanh(t + b2)；

y = a3 ×  ReLU(t + b3)；

y = a4 ×  Softmax(t + b4)

图10，左右位置调整

这里b1，b2，b3，b4都是常数，即不随时间t变化的数，它们对应不同曲线左右位置的调整。鞋匠把b这类数称之为偏置项。鞋匠想验证这些函数的调整应该是简单的：拿出来一张大大的纸，给上面的权重和偏置项选定一些具体的值，在纸上画出了这些新的函数在2维平面坐标系下的曲线，对比原曲线，会发现以上的调整分析是对的。

人工神经网络的形成

有了以上的形式，鞋匠就可以自由地调整每一个神经元的输入和输出了，而一定数量的神经元以某种方式的叠加就可以拟合鞋匠所在2维世界的复杂轨迹了。怎么确定这里的“一定数量”和“某种方式”呢？鞋匠觉得应该是基于对现实问题和科学理论的深刻理解，先给出一个感觉合理的数量和结构，而后经过不停的试验进行验证、改进、再验证，如此循环往复，直到得到自己满意的一个结果。这将是一个漫长的过程，但鞋匠坚信窗外终会雨过天晴。

人类把某类事物放到一起时，一般都会采用分类、分块、分层进行放置，而这些事物的关系一般有一对一、一对多、多对一、多对多等。2维世界里的鞋匠也不例外，他想到了一种众多神经元的排列方式。它是分层的，一共3层，一个输入层，一个隐藏层，一个输出层，并且每一个神经元都和下一层的所有神经元相连，鞋匠称这种连接为全连接，称这种网络为人工神经网络，如图11。

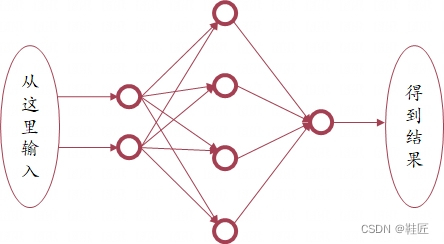
图11，一个全连接人工神经网络

想要这个人工神经网络拟合一个复杂的曲线，首先要选定各神经元的权重，有几个输入就设定几个权重，这些权重分别单独作用于每个输入量上，这样可以对每个输入量单独调整。每个神经元再选定一个偏置量，用于对所有输入量经过权重加权求和后的结果进行调整。鞋匠觉得这个偏置项设计很妙：有了这个偏置项，如果某个神经元来自前一层输入的加权和为0，该神经元也会有个输入，那就是这个偏置量本身，也就是说这个神经元也会对整个神经网络的运算有贡献，因为它有个偏置量作为输入。

鞋匠仔细考虑了下，其实输入层不需要有什么权重和偏置项，这一层真实地反映现实情况即可，它传递真实输入的各项数值，有多少项就有多少个输入点，这就是输入层。鞋匠称这些输入项为输入维度，多少维度就对应多少个输入点，即多少个输入层神经元。接下来鞋匠试图去解决他的问题了，即模拟他在2维世界的生活轨迹，在给定一些现有数值对的基础上，让这个人工神经网络来预测即将到来的下一个时间点上所对应的y值。鞋匠把已经发生的时间点与自己测得的y值记录了下来，形成了真实的现实数据记录。它们是在鞋匠生活轨迹y=f(t)这条曲线上的一些点。这些点都对应着过去的一段时间生活轨迹曲线，未来的事件还没有发生，所以没人知道这条曲线将以什么样的形状发展，但过去已发生的事件形成的轨迹曲线代表着鞋匠生活轨迹的大量信息，让人工神经网络从这些大量已存在的轨迹点上学习，从而学习到鞋匠生活轨迹的某些发展模式，达到能够预测未来事件的目的，即预测即将到来的下一个时间点上所对应的y值。鞋匠记录的生活轨迹点如下，它们是一系列的2维坐标：

X = [[t1, y1]

     [t2, y2]

     …

      [tn, yn]]

这里[t1, y1]代表着一个2维坐标点，这个点是y=f(t)曲线上的一个点，其中t1是过去的某个时间值, y1代表在这个时间值上对应的y值。可以看到X里每一行都是一个2维坐标，第1列代表时间值，第2列代表其对应的y值。X这种表示方式就是数学上的矩阵。这里X这个矩阵的形状就是n ×  2，即n行2列。同样的，如果有人把所有的t值放到第1行，所有对应的y值放到第2行，就会得到一个2 ×  n的矩阵。至于用哪种形式，鞋匠觉得并不重要，但n ×  2是鞋匠喜欢的形状。有了这些实际发生过的现实数据，接下来要做的就是让上面的人工神经网络从这些数据中进行学习。就像人类从孩童时代开始学习，长大后成为社会主义的接班人一样，他的大脑的每个神经元都经过了现实知识的训练，使其成为了某个领域的专家。为了验证网络学习的效果，鞋匠将这些数据分为了两份，一个用来训练网络，一个用来测试网络。用来训练网络的数据集称之为训练集，用来测试网络的数据集称为之测试集。鞋匠的想法大概是这样的，给网络一个输入，如[t1，y1]，他希望网络输出y2这个数值，即下一时刻t2所对应的y值。同样的，给网络下一个输入[t2，y2]，他希望网络输出y3这个数值。于是就形成了这样的期望的输入输出对，如（[t1, y1]，y2），（[t2, y2]，y3）等。这每一个输入输出对，都是一条有效的训练数据，鞋匠称之为一个样本。所有样本，包括训练样本和测试样本，集合在一起，鞋匠称之为样本空间。在训练的过程中，网络会不停的调整，直到网络对于训练集里的所有样本，都能正确输出或者输出达到一定的满意度，就可以用测试集来对网络进行测试了。这就像人类对学生的考试一样，是检验过去一段时间学习成果的一种方式。在对网络进行测试的过程中，不会再对网络进行调整，如果测试的结果令人满意，那么这个被训练过的网络就是鞋匠想要的网络。这时鞋匠把当下这个时刻的时间值t和对应的y值作为输入（即生活轨迹上当下的这个点），便能得到即将到来的下一个未来时间点的y值预测，且这个预测值在一定程度上会是一个令人满意的结果。这是一个不断收集数据、不断优化的过程，会越来越精准。鞋匠觉得他不需要一个完美的网络来精准地看到遥远的未来，只需要今天知道明天股市的结果，那他在这个2维世界里就将羽化成神！

人工神经网络的自我演化

理想是丰满的，而现实是骨干的。想要羽化成神，鞋匠得找到训练他所设计的人工神经网络的方法。鞋匠先把所有的样本以及网络的所有权重、偏置项都以数学的形式展示出来，如图12。

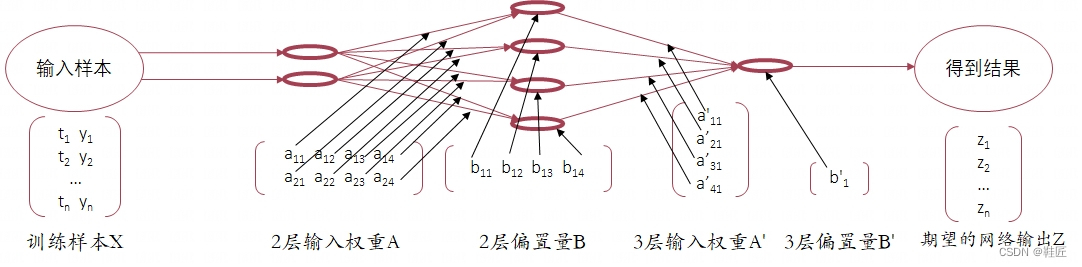
图12，网络样本和参数的数学表示

这里所有神经元输入对应的权重和偏置项统称为人工神经网络的参数，这些参数是在训练过程中被调整的项，直到网络的输出达到满意的程度。上图中的a11，a12，b11，a'11，b'1等就是待调整的网络参数，即需要对权重矩阵A和A'、偏置项矩阵B和B'进行调整。输入矩阵X的每一行都是一个数据样本，权重矩阵A的每一列都对应第2层的一个神经元接收上一层所有神经元输出作为输入的各自独立的加权值，比如，a11即是第2层第1个神经元对应上一层第1个神经元输出的加权值，a21即是第2层第1个神经元对应上一层第2个神经元输出的加权值，b11即是第2层第1个神经元的偏置量，这个神经元在接收上一层所有神经元的输出经过a11和a21加权求和后，加上这个偏置量，最后的求和结果作为该神经元的输入。鞋匠把每个神经元的激活函数定为ReLU（每一层甚至每一个神经元都可以单独赋予不同的激活函数，但实际操作上没有必要这样做，为了计算方便，一般是整个网络或者每一层、每一功能块选择同一种激活函数），以[t1, y1]作为输入为例，来看看整个网络的输出是怎么计算的。在这个计算过程中，鞋匠用·表示乘法运算符。

1）第2层的4个神经元的输入分别为：

I11 = t1 · a11 + y1 · a21 + b11

I12 = t1 · a12 + y1 · a22 + b12

I13 = t1 · a13 + y1 · a23 + b13

I14 = t1 · a14 + y1 · a24 + b14

2）第2层的4个神经元的输出分别为：

O11 = ReLU(I11) = ReLU(t1 · a11 + y1 · a21 + b11)

O12 = ReLU(I12) = ReLU(t1 · a12 + y1 · a22 + b12)

O13 = ReLU(I13) = ReLU(t1 · a13 + y1 · a23 + b13)

O14 = ReLU(I14) = ReLU(t1 · a14 + y1 · a24 + b14)

3）输出层这1个神经元的输入为：

I21 = O11 · a'11 + O12 · a'21 + O13 · a'31 + O14 · a'41 + b'1

4）输出层这1个神经元的输出为：

O21 = ReLU(I21)

对于输入[t1, y1],这里的O21是网络的实际输出，上图中的z1则是期望的输出。这两个值在训练之初是有差异的，这很正常，训练的目的就是缩小这个差异。

同样的，对于上面的4个步骤，如果输入的是所有的训练样本集X，那么：

1）第2层的4个神经元的输入为：

I1 = X·A + B

这个过程即是数学上矩阵间的点积运算和一种神经网络领域特有的加法运算。鞋匠用·来表示点积运算符。这个计算过程的演算示例如下：

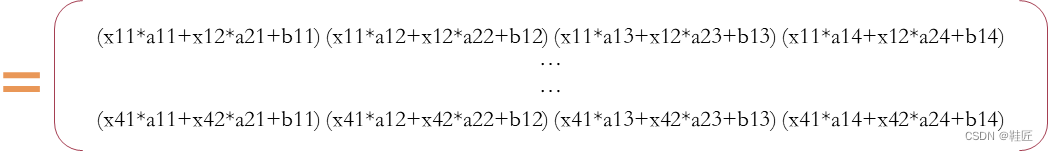
这里X形状为4 ×  2的矩阵，A是2 ×  4的矩阵，得到的结果是 4 ×  4的矩阵。按照以上计算规则，如果两个矩阵可以点积相乘，那么前一个乘数的列数必定要等于后一个乘数的行数，得到的结果的形状以前一个乘数的行数为行数、后一个乘数的列数为列数。

在数学上，严格来讲矩阵的加法应该是对应元素相加，所以两个相加的矩阵必须是行列数相等，但这里的加法实际是将只有一行的B扩展成了4行，扩展的后三行和第一行各元素值都是一样的，而后再做加法运算。鞋匠称这种做法为“广播（Broadcasting）”。

了解了矩阵的运算法则，鞋匠觉得在以下步骤中没有必要再对每个矩阵的运算进行展开了。

2）第2层的4个神经元的输出为：

O1 = ReLU(I1)

3）输出层这1个神经元的输入为：

I2 = O1·A' + B'

4）输出层这1个神经元的输出为：

O2 = ReLU(I2)

对于输入X，这里的O2是网络的实际输出，上图中的Z是期望的输出。它们之间的差异小到一个可接受的范围，鞋匠觉得就算得到了一个训练好的网络。为此，鞋匠定义了一个简单的函数L来衡量这个差异：

                                                        L = Z - O2

                                                           = Z - ReLU(I2)

                                                           = Z - ReLU(O1·A' + B')

                                                           = Z - ReLU(ReLU(I1)·A' + B')

                                                           = Z - ReLU(ReLU( X·A + B ) · A' + B')

鞋匠称这种用来衡量期望的真实值和输出的预测值之间的差异的函数为损失函数。以上就是以损失函数的形式来展示的网络输入输出影射关系的完整的数学表达。鞋匠仔细的思考着，他觉得这里有个弯弯绕。这里的变量是A，B，A'和B'，而训练样本X是固定不变的，它是对实际生活的采样。要调整的就是这些变量，最终使得L落到一个可接受的范围。就上面这个简单的人工神经网络来说，A，B，A'和B'共有17个变化的量，如a11，b11，a'11，b'1等，即这个网络有17个参数。对于任意一个样本来说，X是固定的，需要调整的是这17个参数，使得L差值小到满意的程度。网络训练的过程是对所有的样本一遍一遍的按照同样的规则慢慢调整，直到L差值小到满意的程度。那么L这个函数的自变量就变成了A，B，A'和B'，而因变量就是L了。所以上面的人工神经网络的优化的问题就变成了怎么样寻找到这些自变量的一个具体的数值组合，让L的对所有或者大部分训练样本的计算结果尽可能的小。

这个问题看起来有点复杂，因为这里的自变量太多了，组合将会更多！（如果鞋匠看到后面OpenAI的大模型有1700多亿个参数的话，他可能就不觉得这里17个参数“太多了”）不过鞋匠想，应该将问题简化，先研究简单问题，慢慢总结解决复杂问题的方法。既然这里自变量太多了，那就先研究个简单的，先研究1个、2个或者3个自变量数值组合的求解方法。

先分析1个自变量的情况：鞋匠在纸上画了一个2维平面内的曲线，t是唯一的1个自变量，可以称之为时间变量，横轴就是时间轴，L是因变量，随着时间的变化而变化，它是纵轴。g(t)代表这个函数运算式本身，即L的值是根据这个算式来计算的。如下图。

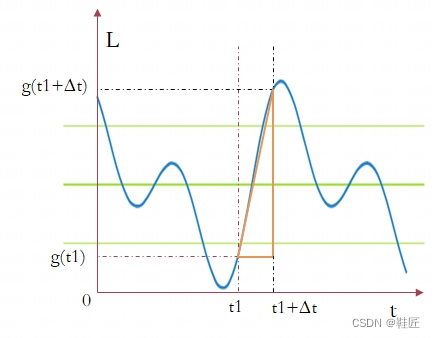
图13，2维曲线变化的快与慢

如果要从这个曲线上的某一个点(t1, g(t1))处把L向着更优化的方向（使得L变小的方向）调整，应该怎么做呢？对于正在看着这条曲线的人类来说，这太简单了，“把t这个自变量向左调整”，这是人类瞬间给出的答案，它是如此的明显，毫不费力，向左调整就可以得到更小的L。但鞋匠的世界是2维的，他无法跳出这个平面来观察这个世界，作为2维世界的科学家，他觉得需要找个科学的方法来解决问题。于是，鞋匠开始研究曲线在(t1, g(t1))这个位置上是如何变化的，即L随着t的变化关系，比如L随着t在t1这个点的变化是快还是慢？是减小还是变大？鞋匠首先假设时间t在t1处增加了一个小小的增量，以Δt表示，那么L这个量就会由g(t1)变化到了g(t1+Δt)，如上图所示，那么衡量L随着t增加而变化的快慢就可以这样来表示

(g(t1+Δt) – g(t1)) / (t1 + Δt – t1) = (g(t1+Δt) – g(t1)) / Δt

即用L的变化量与t的变化量相比，用这个比值来衡量L随着t变化的快慢。鞋匠先用D来表示上面这个表达式的值，D越大表示L在Δt一定的情况下其变化量就越大，D越小就代表L在Δt一定的情况下其变化量就越小。怎么判断L是变大了还是变小了呢？仔细想下，如果g(t1+Δt)比g(t1)大，就意味着L变大了，如果g(t1+Δt)比g(t1)小，就意味着L变小了。那么在变大的情况下，D就是正值，而变小的情况下，D就是负值。太好了，鞋匠想可以用D的正负来判断L是变大还是变小。现在，鞋匠可以确定L在(t1, g(t1))这个点随着t变化而变化的快与慢，以及变大还是变小了。如果想把L向着更小的方向调整，那就看D的正与负，如果是正值，那么把t向左侧调整，即把t调小一点，如果是负值，那么把t向着右侧调整，即把t调大一点。而调整的幅度正好可以根据L变化的快与慢来调整，如果L在这个点的变化很快，即D在不考虑正负的情况下其值很大，可以把t的变化幅度（即Δt）调整的大一点，因为L在该点处向着最小值的方向比较明显，t调整的大一点可以快速接近L的最小值。如果L在这个点的变化的慢，即D在不考虑正负的情况下其值很小，可以把t的变化幅度（即Δt）调整的小一点。在这种情况下L最小值的方向不明显，形势不明朗的情况下，就要慢慢调整。可以看到，这里衡量L变化的快与慢是在不考虑D的正与负的情况下，仅看D的大小来判断的，在数学上，鞋匠把D的大小这样的数值称之为D的绝对值。鞋匠觉得自己找到了正确的路。

导数的诞生

“如果”，鞋匠继续研究着，“如果让Δt无限趋近于0呢”？那么D会怎么变化呢？在这种情况下D的变化是不是就可以看作在(t1, g(t1))这个点的变化呢？鞋匠用lim这样一个符号来表示这个Δt趋于0的过程，如下

之所以使用lim，这和多年前鞋匠学过的一个英文单词limit有关，鞋匠觉得这不重要，重要的是后面都用这个符号来表示这个过程就好了。鞋匠认真的思考着，他觉得自己已经进入了一个崭新的的世界，那里有着众多的“无限”，无限大（正无穷大或者负无穷大），无限小（无限接近于0），而这些“无限”之间的关系又是那么的朦胧：两个无限大哪个大？两个无限小哪个小？无限大除以无限大等于1吗？无限小除以无限小呢？无限大乘以无限小是向着无限大变化还是无限小变化还是有其它的选项？这些值得研究下。

鞋匠在纸上写下了几个无限的例子：

                                                        E1 = 

                                                        E2 =

                                                        E3 =

                                                        E4 =

                                                        E5 =

                                                        E6 =

这几个表达式都比较直观。这里x无限趋于0而不等于0。当x趋于0时 、 、 也会趋于0，而 和 变得无穷大， 则趋于1/1000。鞋匠称0为 、 、 的极限，1/1000为 的极限，即E1，E2，E3都等于0，E6等于1/1000,而符号lim就代表求解极限的运算。两个趋于无限小的数相比可能是无限大，比如E2/E1 =   趋于无限大，也可能是某个固定的值 ，比如E3/E2 =   =   = 2，无限大乘以无限小可能趋于无限大，比如E2 ×  E5 =  ；也可能趋于无限小，比如E1 ×  E4 = 。所以鞋匠觉得无限大处和无限小处需要具体情况具体分析，对于能趋于某个固定值情况，鞋匠称之为收敛，这个固定值即是它的极限，对于不能收敛到一个具体值的情况，鞋匠称之为发散。

同样的，上面衡量L随着t在(t1, g(t1))点变化快慢的过程，也是一种求其极限的过程，即

这个极限值可能是一个具体的数，即它是收敛的，也可能趋于无穷大，即它是发散的。当它可以收敛时，它就能精确地表示L随着t在(t1, g(t1))点变化的快慢。回到图13的那条曲线，这个极限值就是曲线g(t)在(t1, g(t1))处的切线的斜率。斜率就是衡量一条直线在一个2维平面内的倾斜程度，转化为变化的快与慢的概念时，可以把这个斜率理解为因变量随着自变量变化的快慢。以图13的坐标系为例，即是L随着t变化而变化的快慢，只是对一条直线来说，这种变化率是不变的，所以这个斜率在直线上所有的点都是一个固定值。这种求极限的过程，就是确定L随着t在(t1, g(t1))点变化的快慢的过程，在数学上，鞋匠称之为求导过程，即求在(t1, g(t1))点处L对t的导数。鞋匠意识到自己已经来到了微积分的世界。数学上，导数一般表述为 ，可简单的表示为 ，更一般的，在数学教科书上常见的是 ，称之为y对x的导数。所以，可以把刚刚求解L变化的快慢过程描述为求解L对t的导数的过程。这个过程对曲线上所有的点都是一样的，只是不同的t点，可能对应不同的导数值，也就是说这个导数值是随着t的变化而变化的。等等！鞋匠意识到这里的导数 也是对应着一个自变量为t的函数，鞋匠将这个函数表示为  =  = 。有了这个函数 ，只要给出任意一个t点，鞋匠就能通过 计算出g(t)在t点处的导数。

还记得上面推导的D的正与负、大与小（绝对值大小）代表着什么吗？这里可以用L在(t1, g(t1))点的导数，即 ，重新描述一下。 的绝对值越大，就代表曲线g(t)在t1点的切线的斜率越大，L（即g(t)）在该点的变化越快。 的绝对值越小，就代表曲线g(t)在t1点的切线的斜率越小，L（即g(t)）在该点的变化越慢。当 为正时，要使L变得更小，就应该把t向左调整，即把t减少一个量，当 为负时，要使L变得更小，就应该把t向右调整，即把t增加一个量。

至此，鞋匠觉得在1个自变量的世界里一片晴空万里，他可以轻松地优化L，使其向着更小的方向调整。

偏导数与梯度

但这还不够！在上面鞋匠的人工神经网络的例子中，有

L = Z - ReLU(ReLU( X·A + B ) · A' + B')

这里有17个自变量，鞋匠的目的是确定这17个自变量的值，在这些值固定不变的情况下，带入每个一X中的样本数据后，得到的L值都比较小，或者绝大多数都比较小，这个“小”要小到让鞋匠满意的程度。

所以鞋匠继续着自己的研究，他又增加了一个自变量，即研究一个因变量随着两个自变量而变化的情况。仔细想下，L = g(x)，是一个2维平面的曲线，这里相对于上面的例子只是把t换成了x，但道理都是一样的。L = g(x)表示在横轴为x、纵轴为L的2维平面里的一条曲线。现在增加一个自变量，写成 L = h(x, y)，这里x和y是两个自变量，它们各自可以独立的变化，而L随着x和y的变化而变化。注意，上面的两个L是不同的，这样写是为了体现L不断增加自变量个数的过程。L = g(x)是一个2维平面的曲线，L = h(x, y)呢？它代表了什么？鞋匠发现上面 L = g(x)里有两个变化的量，而这两个量可以对应到一个平面。平面是2维的，即鞋匠的世界，那里只有前后（维度L）和左右（维度x）。相对应的，L = h(x, y)一共有3个变化的量，分别是L，x和y，那么三个变化量的L = h(x, y)则可以对应人类的3维世界，那里不仅有前后（维度y）、左右（维度x）还有上下（维度L）。所以L = g(x)是2维世界的一条线（或直或曲），L = h(x, y)是3维世界的一个面（或平或曲）。鞋匠无法看到3维世界，但他在2维世界里近似的画出了L = h(x, y)在3维世界里的一个曲面，如图14。

图14，3维空间中确定下降速度最快的方向

上图中两个山丘的表面就是L = h(x, y)所描述的在3维世界的一个曲面。鞋匠已经知道，对于一个自变量的情况，要判定在某个点处如何调整，可以通过在这个点处求解导数的方法来确定自变量的调整量以及向哪个方向调整。现在是两个自变量，怎么确定调整方向和调整量呢？化繁为简一直都是鞋匠解决问题的思路，就像上面的“复杂是简单的叠加”一样。鞋匠想，x和y两个自变量同时变化问题就会变得比较复杂，何不先固定一个，这样的话，问题就退化成了一个自变量的情况。太好了，这是个好方法，鞋匠感受到离答案不远了。

鞋匠在上图的一个山坡上确定了一个点，（x1, y1, L1），看看在这个点处如何确定x和y应该如何调整，使得L向着更优化的方向（更小的方向）变化。按照化繁为简的思路，鞋匠先把y = y1固定不变，即现在只有x在变化，L随着x的变化而变化，于是L = h(x, y)在这种情况下就变为 L = h(x, y1)，这里的y1不再变化。这就变成了一个自变量的情况，可以按照上面推理的求导过程来确定x的调整方向和调整量，即L在点（x1, y1, L1）处对x求解y固定为y1时的导数。鞋匠觉得有必要设计一个新的符号来表示这里的导数，以区分刚刚的 这种形式，如下：

 =  也可以表示为

同样的，按照上面的描述，鞋匠注意到，  绝对值越大，就代表在y = y1的情况下，L随着x的变化越快，即L在这个点向着最小值的方向上形势十分明朗，所以x的调整幅度可以大一点，  为正则代表x要向着x轴的负方向调整，即x要减少一个量，  为负则代表x要向着x轴的正方向调整，即x要增加一个量。怎么理解这个过程呢？鞋匠想 ，在2维平面内，只有前后、左右，如果固定一个维度的值，比如固定左右，那么就只能在前后这个方向上移动，这样才能保证在左右方向上始终保持在这个固定值上，在这种情况下原本可以在一个面上的移动就退化称了只能在先前或者向后这一条线上移动了。在3维空间中，有3个维度，前后、左右和上下，如果固定一个维度的值，比如上下，那就只能在前后、左右这两个方向或者维度上移动了，在这种情况下原本可以在一个立体的空间内的移动就退化成了只能在一个等高的平面上移动了，此时3维的问题就退化为了2维问题。所以L = h(x, y)代表了一个曲面，这个曲面有左有右、有前有后、有高有低，固定住y值，即令 y = y1就意味着与y轴对应的“前后”被固定了，只能左右和上下移动了，从数学上看，就意味着在这个曲面上只有y = y1的点才是符合要求的点，这些点连在一起是一条在这个曲面上的一条线，也可以说是这个曲面在y = y1这个平面上的投影。和L = g(x)一样，这个投影也是一条曲线。所以在y = y1的情况下，问题就退化成了求解一条曲线上某个点处的导数的过程。这种导数显然和 是不同的，鞋匠称这种先固定一个维度的值（或者固定多个维度的值）然后求解出来的导数为偏导数，  。

鞋匠觉得到这里有必要重点备注下，是时候来正向理解导数了。上面一直都是从使得L变小的角度来分析问题，而导数或者偏导数的正与负，恰恰和L变小的调整方向是相反的。导数或者偏导数为正时，其对应的变量的调整方向为负，即往该自变量的负方向调整，该自变量要减少一个量。导数或者偏导数为负时，其对应的变量的调整方向为正，即往该自变量的正方向调整，该自变量要增加一个量。如果正向来理解导数或者偏导数的话，导数和偏导数的正负正好指示了L随着自变量x或y增速最快的方向，导数或者偏导数为正，则表示随着自变量的增加L有个正增速，即增大，导数或者偏导数为负，则表示随着自变量的增加L有个负增速，即减小。这一点很重要，鞋匠用带箭头的线段来表示所求解的偏导数，线段的长度代表L的增速，即L随着该自变量增加而变化的速度，而线段的箭头代表导数所确定的在该维度上所对应的自变量增加时，L增加的方向。

如图14， 用一个线段来表示就是紫色的那条线段。可以看到，在y = y1的情况下，L只随着x的变化而变化，所以偏导数 所确定的方向只是体现了在x轴上的调整，其方向代表了L随着x增加而增加的最快的方向。鞋匠按照同样的方法，把x值固定，即令 x = x1 不变，得到了L对于y的偏导数  ,并用带有方向的蓝色箭头标注在了图14里。带箭头的蓝色线段表示L在y轴上随着y的增加而增速最快的方向以及增速大小。

看到这两个带箭头的线段这让鞋匠想起了在物理学上学到的求解合力的过程。想象一下，一个人的双手分别被两个朋友用力的拉着，一个向着左前方拉，一个向着右前方拉，假设他们的拉力大小是一样的，用力的方向和这个人的正前方的夹角也是一样的，那这个人会向着正前方移动；如果右手受到的拉力大，这个人就会向右偏，如果左手受到的拉力大，这个人就会向左偏；如果力量大小保持不变，而右手拉力的方向更偏向右侧，这个人就会向右偏，同样在双手力量大小保持不变的情况下，左手拉力的方向更偏向左侧，这个人就会向左偏，如图15所示。

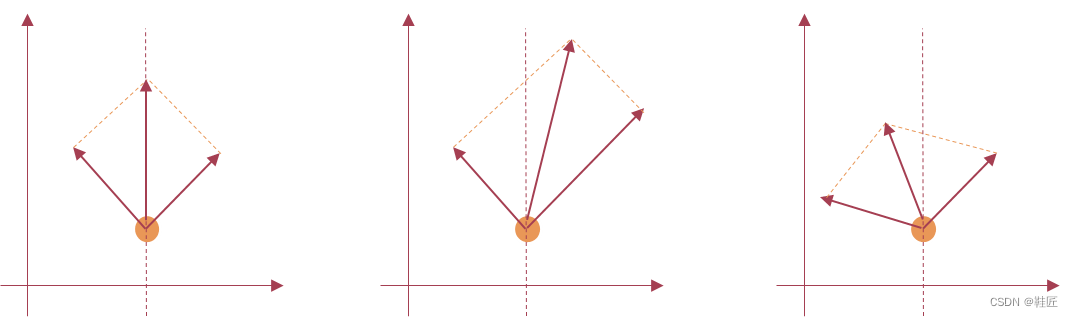
图15，合力的演示

上图中，带有箭头的线段的长短表示力的大小，箭头的方向代表拉力的方向，中间的带有箭头的线段代表的是左右两侧的两个力的合力方向和大小。这种根据两侧力的方向和大小确定的方向是最佳的合力方向，所确定的合力大小也是最大的大小。同样的，鞋匠把图14中紫色线段和蓝色线段合起来，最后的作用效果就是红色线段所表示的那样，代表着 和 合在一起所决定的L的增速方向和增速大小。这是一个“合”在一起的量，它既有方向也有大小，鞋匠把这种既有方向也有大小的量称之为向量，并用如下的形式来表示：

( ， )

这个向量所标识的方向是 和 这两个分量合在一起所决定的L的最佳的增速方向，而其合在一起的大小所决定的也是最大的增速大小。鞋匠把这种最佳的方向和最大的“大小”（最快的增速）称之为在这个点处的梯度。在图14中，点（x1, y1, L1）的梯度方向就是红色箭头所指示的方向，即L随着x和y的增加其增速最快的方向。那么，回到鞋匠的人工神经网络的调整这个问题上来，要优化L使得其变得更小，就要沿着与在这个点处的梯度相反的方向调整，而这个相反的方向就代表着在这个山坡上沿着这个方向调整x和y，L的下降速度将是最快的，如图14带箭头的白色线段所示。

现在鞋匠找到了一个方法，利用这个方法可以不停的增加自变量个数，每增加一个自变量，函数L所描述的空间图形就增加一个维度，并且在固定住一些自变量值的情况下，问题可以最终退化为2维曲线在一个点处的求导问题。这样逐一求解各个自变量在某个高维空间的一个点处的偏导数，把这些偏导数组合成一个向量，这个向量所确定的梯度方向就是L随着所有自变量增加而增速最快的方向，如果要使得L变小，那就沿着与这个梯度向量的方向相反的方向调整。这简直太棒了！对于上面17个自变量的损失函数L，如果要调整L使得其变小，鞋匠觉得确定好其梯度向量就好了。

求导链式法则

仔细看了下这个损失函数L，鞋匠又遇到了一个难题，这个L函数是一个函数嵌套，即ReLU的函数里又嵌套了一个ReLU函数，即便是上面的三层神经网络中第二层和第三层的激活函数不一样，也会有这个嵌套，只是一个函数嵌套了另一个不同的函数而已。

L = Z - ReLU(ReLU( X·A + B ) · A' + B')

上面这种嵌套关系为求解偏导数带来了困难。鞋匠称这种有着嵌套关系的函数为复合函数，比如，y=f(g(x))。假设u=g(x)，则复合函数y=f(g(x))=f(u)，这样就可以把一个复合函数转变为两个单变量的函数，一个是u=g(x)，一个是y=f(u)，其中u是中间变量，而x和y分别就是自变量和因变量，鞋匠的目标就是找到y对于x的导数，即   。

鞋匠知道，u关于 x的导数是 ​，而y关于u的导数是 。现在，考虑y是u的函数，而u又是x的函数，因此y是通过u再通过x而变化的，先是由x的变化∆x引起的u的变化∆u，再由u的变化∆u引起y的变化∆y，按照求导即求极限的思想，得到：

 

按照上面的分析，导数其实就是在某点处因变量对于自变量的变化率，所以在自变量变化某个极小值的时候，因变量的变化量就近似地等于变化率乘以自变量的变化量，如果以∆y 和∆u 为例，则有：

同理，∆u 和∆x 的关系可表示为：

因此，

​​​​​​​​​​​​​​

由此看出，对于一个复合函数来说，因变量对于自变量的导数等于因变量对于中间变量的导数乘以中间变量对于自变量的导数。有了这个变换关系，鞋匠的网络优化就可以顺利推进了。鞋匠很高兴，他把这种求导关系称为链式法则。

在链式法则下，再来看看原复合函数L：

L = Z - ReLU(ReLU( X·A + B ) · A' + B')

这里可以把ReLU( X·A + B )看作一个中间变量u，即令

u = ReLU( X·A + B )

那么，L就是待求导的复合函数，有：

L = Z - ReLU(ReLU( X·A + B ) · A' + B') = Z – ReLU(u· A' + B')

这种形式看起来就简单多了，鞋匠注意到，这里的u其实就是上面那个人工神经网络第2层神经元的输出，u随着A和B的变化而变化。以上人工神经网络的优化就简化为求解以下函数的偏导数

L = Z – ReLU(u· A' + B')

即求解L关于u（随着A和B变化而变化的中间量）、A'和B'的偏导数，其结果构成的梯度向量可表示为：

这里 是一个中间结果，它包含了L关于A（a11, a12, a13, a14, a21, a22, a23, a24）和B（b11, b12, b13, b14）的变化率信息。以上向量中的6个元素的求解，都是按照先固定其它5个参数，把原L函数转化为一个2维曲线的方式，即一个因变量和一个自变量的函数形式来求解各自偏导数的。可以看到，在这个向量里，鞋匠确定了人工神经网络的最后一层神经元的参数（A'和B'）如何调整，才能使得L向着小的方向调整，那就是根据  ,  ,  ,  , 这些偏导数所确定的各个分量的方向（正向调整还是负向调整）和大小（变化率）对A'和B'进行调整。

接下来，为了确定第2层神经元的参数（A和B）如何调整，鞋匠需要求解出L关于A和B的变化率，即偏导数，才能确定如何调整A和B。按照链式法则，鞋匠最终得到了L关于A和B的偏导数，如下：

现在一切都已尘埃落定，鞋匠把所有的偏导数放到一起得到：

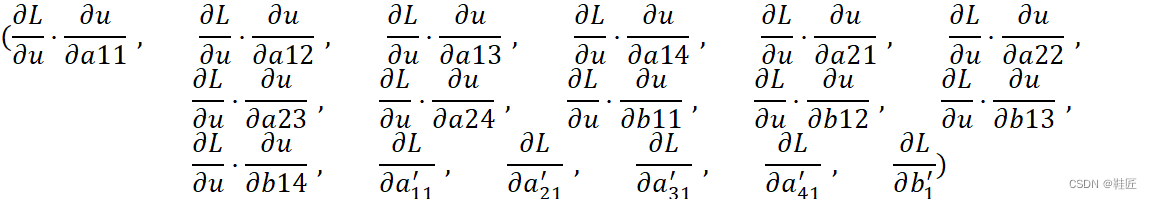
这就是最终的整个神经网络全局的所有网络参数的一个梯度向量，它有17个元素，对应17个神经网络参数，鞋匠把它称为17维的高维梯度向量。该向量方向的相反方向即是优化L使其变得更小的最快的方向。

反向传播算法

前面A，B，A'和B'都是按照矩阵的形式表示的，为了更方便地利用矩阵运算调整它们，鞋匠把这些偏导数也写成了矩阵的形式，如下

​​​​​​​ ​​​​​​​

      ​​​​​​​

​​​​​​​

​​​​​​​

​​​​​​​

由上面的过程，可以看出，神经网络的优化过程，是一层一层进行优化的，从后往前依次求解偏导数，直到所有神经网络参数的偏导数求解完成，最终形成一个巨大的高维梯度向量。鞋匠称这样的由后往前的调整方式为反向传播算法。

这样，神经网络的优化就变得简单了，每个参数的调整，就是按照该参数所对应的在该维度上的梯度向量的分量来调整，即根据其所对应的偏导数进行调整，以a11为例，L关于a11的偏导数为 ，这个偏导数代表了L随着a11增加而增加的增速，鞋匠觉得不能以这个增速的大小本身来作为a11的调整量，而应该有个系数来约束a11的调整量，就像不能拿一辆车的行驶速度来作为其行驶的距离的衡量一样，在同一速度下，所经历的行驶时间不同，得到的行驶距离（距离增量）也不同。同样的，不同的系数乘以偏导数值，就可以得出不同的调整量，这样就可以控制调整量的大小，即控制整个神经网络的优化速度了。鞋匠称这个系数为学习率，那么a11的调整可以表示为：

a11new = a11old - η·

这里η就是学习率，a11new表示a11调整后的值，a11old表示a11调整前的值。按照上面总结出的规律，鞋匠验证了下这个式子是否正确： 为正时，表示a11需要往小的方向调整，即新的a11需要在原来的基础上减去一个正量，在这种情况下，上面的式子是正确的。 为负时，表示a11需要往大的方向调整，即新的a11需要在原来的基础上加上一个正量，在这种情况下，上面的式子也是正确的，因为减去一个负值，相当于加上一个正值。把同样的算法应用到所有的参数矩阵，鞋匠得到了网络所有参数的调整如下：

Anew = Aold - η·∇A

Bnew = Bold - η·∇B

A'new = A'old - η·∇A'

B'new = B'old - η·∇B'

Anew代表调整后的第2层神经元的输入权重矩阵，Aold代表调整前的第2层神经元的输入权重矩阵；Bnew代表调整后的第2层神经元的输入偏置项矩阵，Bold代表调整前的第2层神经元的输入偏置项矩阵；A'new、A'old和B'new、B'old则分别代表第3层神经元调整前、调整后的输入权重矩阵和偏置项矩阵。

可以看到，η也是一个需要确定的参数，但这个参数和A、B等网络参数不同，它的大小决定了调整量的大小，即影响调整过程，而不会影响网络实际需要调整哪些参数，以及调整到什么程度。鞋匠称η这样的参数，为人工神经网络的超参数，简言之就是控制参数调整的参数。

利用以上的调整公式，鞋匠就可以调整所有网络参数了，但鞋匠觉得可以采用不同的策略，比如：

1）对于整个训练样本集X里的每一个样本，都计算一次损失函数关于所有参数的梯度，然后按照所有梯度的平均值来更新参数。这意味着参数的每次更新都需要遍历整个数据集，计算成本较高，尤其是在大规模数据集上，计算量更大。鞋匠称这种方法为批量梯度下降法。

2）与批量梯度下降法不同，还可以在每次迭代时仅使用一个样本来更新参数。即从训练集中随机选择一个样本，计算该样本作为输入时损失函数对所有参数的梯度，并据此更新参数。这种方法的优势在于计算速度快，可以在每次迭代时快速调整参数，适合大规模数据集。缺点是更新路径可能较为波动，因为每一步的梯度都是基于单个样本来计算的。鞋匠称这种方法为随机梯度下降法。

3）如果把前面两种方法一起考虑进来做一个折衷方案，就可以这样来调整：在每次迭代时使用数据集中的一部分样本来计算梯度，这个部分称为小批量，而小批量的大小（通常为几十到几百）是一个超参数，需要手动设置。这种方法结合了批量梯度下降的稳定性和随机梯度下降的高效性，既能减少计算量，又能保持较好的收敛性能。鞋匠称这种方法为小批量梯度下降法。

至此，鞋匠觉得似乎所有的问题都已解决！

调整、步长与宏观想象

但刚刚引入的超参数η还是比较朦胧，它犹抱琵琶半遮面，羞涩地不肯露出真容。鞋匠仔细地回忆着这个调整过程，在2维空间中，调整是为了寻找L曲线上那个全局的波谷，在3维空间中，调整就是为了寻找L曲面上那个最低的山谷，而η所决定的就是每次每个参数调整的步长，这个有什么实际意义呢？想象下，如果步长很小，那直观的感受是，整个网络的调整会很慢，但还有一个问题值得思考。先考虑2维曲线的情况，如图16，一般一个网络的参数一开始都是随机初始化的，也就是说网络参数一开始可能正好落在橙色的点处，网络需要基于这个点进行训练，并找到最低点。假设由η计算出的步长是1，整个网络的调整过程中，它最终可能落于橙点右侧的波谷的某处，但永远也无法翻越这个波谷两侧的波峰，因为其步长是1，而这个橙色的初始点离两侧的波峰处都大于1，网络的调整策略是一次调整一个步长来寻找下一个更为低的点，所以在这种情况下，a的调整被限定在了这个波谷里。如果初始化的点在蓝点处，在步长为1时，L就可以被优化到更低的点，所以网络的训练效果和初始化有着很大关系。如果想跨出橙色点所在的波谷，就需要把步长调整的更长，比如步长为6，就可以轻松的跨出橙点所在的波谷，但又带了另一个问题，假设蓝点右侧的波谷是全局最优点，那很难经过调整进入这个谷底，因为这个波谷在步长为6的情况下也很容易被跨过去。在3维的情况下，就是寻找最低的山谷的过程，这里步长同样有着类似的作用，步长太长容易跨过最低的山谷，步长太短则容易陷入局部最低点。可以想象，更高维也会有类似的情况，比如上面的17维空间，在如此高的维度里，寻找最低点会变得更为复杂。由此可见，η的意义重大，直接影响着是否能有效地找到最低点，也就是说使得L最小的点，也就是所有确定好的网络参数值组合在一起使得在X样本数据下L最小。鞋匠意识到，一般情况下，特别是在高维空间中，很难找到全局最优，那人类世界里出现的大模型呢？那可是1700多亿个参数的网络，鞋匠感觉脑袋要炸裂一般，在如此高的维度下，那究竟是一个怎样的世界呢？所以要解释一个拥有高维参数空间的人工神经网络，何其难啊！

图16，步长的作用

全局最低点就是最优的吗？是不是说经过训练的网络对于训练样本输出的预测值与期望的真实值的差越小越好呢？也不见得，那可能导致这个网络被训练的太规矩了，以至于只认得训练过的样本，而对于测试样本计算出来的预测值与期望的真实值差距较大，鞋匠称之为过拟合！不过，出现这种情况也可能是所选择的训练样本不能代表整个需要模拟的曲线，或者说这些样本不能代表那个巨大的样本空间，或者网络结构设计的过于简单或者过于复杂，或者网络结构不适合解决这个问题，等等。鞋匠觉得越想越复杂了，还是回到要解决的原始问题上比较好。

回到鞋匠的生活轨迹上来，鞋匠对以上的分析以及由此而得出的训练人工神经网络的方法很满意。通过以上方法，他训练得到的人工神经网络，可用于预测他的生活轨迹，预测2维世界的股市变化等等，这种预测的效果是令人满意的，会随着时间的推移越来越精准的。在鞋匠的2维世界里，他已化身为神！

>>下一章节：《鞋匠的AI之旅》- 3. 词嵌入

<< 内容总纲：《鞋匠的AI之旅》- 总章【一段从神经元到GPT的AI之旅】