线性代数的本质（Essense of Linear Algebra）——3Blue1Brown

视频资料：https://www.bilibili.com/video/av6731067

一、向量是什么

• 物理专业：向量是空间中的箭头，由长度和方向决定
• 计算机专业：向量是有序的数字列表
• 数学家：向量可以是任何东西，只要保证向量相加、数字与向量的相乘有意义即可

（1）当在坐标系下以有序多元数组的形式表示向量时，不同位置上的数字代表在相应坐标轴上的投影长度

（2）当把向量视作一种运动时，向量加法可以视为依次进行各个运动，即向量的首尾相连，反映到数值上，就是对应数值项的相加

（3）从几何角度看，向量数乘就是向量的缩放，反映到数值上，就是各个数值项都乘以标量

（4）线性代数的两种基本运算：向量加法和向量数乘

二、线性组合、张成的空间、基

（1）向量：基向量根据坐标值进行缩放并相加的结果　　//用数字描述向量时，都依赖于当前采用的基

（2）线性组合（数乘和加法）：两个数乘向量的和（二维）　　$a\vec{v}+b\vec{w}$　　//缩放再相加

注：线性的一种解释——当固定其中一个标量$a$时，让另一个标量$b$自由变化时，组合向量的终点会形成一条直线

（3）向量张成的空间：给定向量所有线性组合向量的集合

（4）线性相关：存在某向量可以表示为其他向量的线性组合 $\vec{u}=a\vec{v}+b\vec{w}$，即此向量落在其他向量张成的空间中，可以移除而不减小张成的空间

（5）线性无关：所有向量都给张成的空间添加新的维度

（6）基：向量空间的一组基是张成该空间的一个线性无关向量集

三、矩阵与线性变换

（1）变换与函数类似，接收输入，生成输出，变换隐含可以用运动的思想进行理解

注：此处变换接收一个向量，并输出一个向量，可以视为将输入向量移动到输出向量

（2）线性变换的特殊之处：变换保持网格线平行且等距分布

• 所有直线在变换后仍然保持为直线，不能有所弯曲
• 原点位置必须保持固定

（3）线性变换只需要记录基向量$\hat{i}=\begin{bmatrix}1 \\ 0\end{bmatrix}$ 和 $\hat{j}=\begin{bmatrix}0 \\ 1\end{bmatrix}$ 变换后的位置　　　

注：线性变换由它对空间基向量的作用完全决定

（4）重要推论：因为线性变换网格线平行且等距分布，所以变换前后向量关于基向量的线性组合保持不变！

假设原始向量为$\begin{bmatrix}x \\ y\end{bmatrix}$,当基向量$\hat{i}=\begin{bmatrix}1 \\ 0\end{bmatrix}$和 $\hat{j}=\begin{bmatrix}0 \\ 1\end{bmatrix}$变为$\hat{i}=\begin{bmatrix}1 \\ -2\end{bmatrix}$和 $\hat{j}=\begin{bmatrix}3 \\ 0\end{bmatrix}$时，原始向量变为：

$$\begin{bmatrix}x \\ y\end{bmatrix} \rightarrow x\begin{bmatrix}1 \\ -2\end{bmatrix}+y\begin{bmatrix}3 \\ 0\end{bmatrix}=\begin{bmatrix}1x+3y \\ -2x+0y\end{bmatrix}=\begin{bmatrix}\color{red}1 & \color{red}3\\ \color{red}-\color{red}2 & \color{red}0\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix}$$

可以看出，二维线性变换仅由四个数字完全确定，而这四个数字对应于基向量变换后的坐标

因此，可以看出矩阵就是对线性变换的一种描述，其中不同列表示不同基向量变换后的结果；矩阵的乘法视为变换后基向量的线性组合　　//矩阵向量乘法用于计算线性变换作用于给定向量的结果

$$\begin{bmatrix}\color{red}a & \color{blue}b\\ \color{red}c & \color{blue}d\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix}=x\begin{bmatrix}\color{red}a \\ \color{red}c \end{bmatrix}+y\begin{bmatrix} \color{blue}b\\  \color{blue}d\end{bmatrix}=\begin{bmatrix}{\color{red}ax }+\color{blue}by\\ {\color{red}cx}+\color{blue}dy\end{bmatrix}$$

注：矩阵代表对空间的一种特定线性变换

四、 矩阵乘法与线性变换复合

（1）矩阵乘法的几何意义：两个线性变换相继作用的合成　　//独立变换的“复合变换”

（2）追踪基向量的变化：

$$\begin{bmatrix}\color{red}a & \color{red}b\\ \color{red}c & \color{red}d\end{bmatrix}\begin{bmatrix}\color{blue}e & \color{blue}f\\ \color{blue}g & \color{blue}h\end{bmatrix}=\begin{bmatrix}ae+bg & af+bh\\ ce+dg& cf+dh\end{bmatrix}$$

基向量$\hat{i}=\begin{bmatrix}1 \\ 0\end{bmatrix} \rightarrow \begin{bmatrix}e \\ g\end{bmatrix} \rightarrow \begin{bmatrix}\color{red}a & \color{red}b\\ \color{red}c & \color{red}d\end{bmatrix}\begin{bmatrix}e \\ g\end{bmatrix}=\begin{bmatrix}ae+bg\\ ce+dg\end{bmatrix}$

基向量$\hat{j}=\begin{bmatrix}0 \\ 1\end{bmatrix} \rightarrow \begin{bmatrix}f \\ h\end{bmatrix} \rightarrow \begin{bmatrix}\color{red}a & \color{red}b\\ \color{red}c & \color{red}d\end{bmatrix}\begin{bmatrix}f\\ h\end{bmatrix}=\begin{bmatrix}af+bh\\ cf+dh\end{bmatrix}$

（3）矩阵乘法不符合交换律，但满足结合律

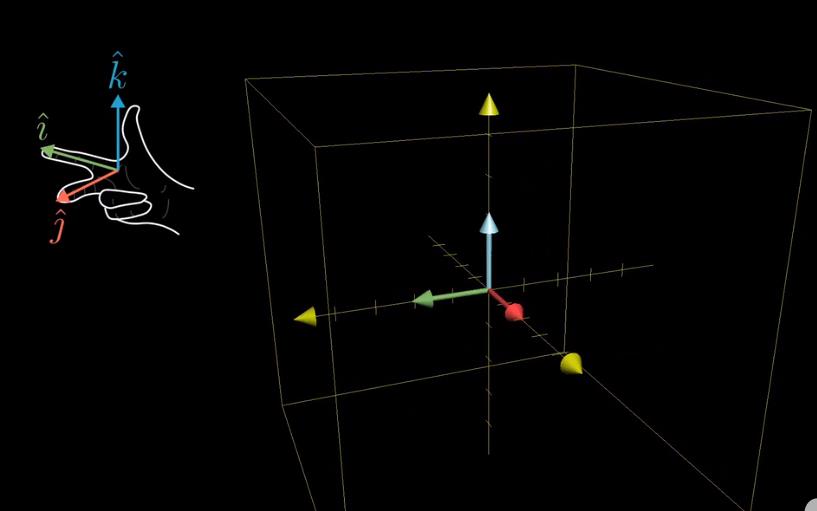
附注1——三维空间中的线性变换：追踪三维基向量的变化　　//三维方阵

五、行列式：线性变换改变面积的比例　　//三维为体积的缩放

（1）含义（绝对值）

• 给定区域面积增大或减小的比例　　
• 空间拉伸或挤压的程度
• 单位正方形的面积变化比例

（2）矩阵行列式为0：对应变换将空间压缩到更低的维度　　//列线性相关

（3）行列式的正负号：对空间定向orientation的改变，定向发生改变则为负

注：

• 可根据基向量$\hat{i}$和$\hat{j}$进行考虑，$\hat{j}$位于$\hat{i}$左侧为正，$\hat{j}$位于$\hat{i}$右侧为负
• 三维空间的定向：右手法则；如果变换后不符合右手法则，符合左手法则，则行列式为负

（4）计算行列式：$$det\left(\begin{bmatrix}a & b\\c & d\end{bmatrix}\right)=ad-bc$$　　//二维方阵

 六、逆矩阵、列空间与零空间

（1）求解常系数线性方程组 $A\vec{x}=\vec{v}$

$$\begin{array}{c} 2x+5y+3z=-3\\4x+0y+8z=0\\1x+3y+0z=2\\\end{array} \rightarrow \begin{bmatrix}2 & 5 & 3\\4 & 0 & 8\\ 1 & 3 & 0\end{bmatrix} \begin{bmatrix}x\\y\\z\end{bmatrix} = \begin{bmatrix}-3\\0\\2\end{bmatrix}$$

方程$A\vec{x}=\vec{v}$的几何含义：寻找向量$\vec{x}$，使得其经过变换$A$后得到向量$\vec{v}$

（2）行列式$det(A)\neq 0$时　　//唯一解

有且仅有一个向量满足该变换$\vec{x}=A^{-1}\vec{v}$

此时存在逆变换$A^{-1}$，满足$A^{-1}A=I$（恒等变换） 

（3）行列式$det(A)=0$时

• 有解的条件：向量$\vec{v}$位于变换后的低维空间内　　//列空间

（4）列空间：变换后的基向量（矩阵的列）所能张成的空间 $A\vec{x}$　　//解决“何时存在解”

• 一定包含零向量

（5）秩rank：变换后的空间的维数　　//列空间的维数

• 满秩full rank：秩与列数相等；列空间的维数与输入空间的维数相等
• 对于满秩矩阵而言，只有零向量在变换后仍落在原点处
• 对于非满秩矩阵，存在多个向量变换后落在原点

（6）矩阵的零空间（核kernel）：变换后落在原点的向量$\vec{x}$集合，即满足$A\vec{x}=\vec{0}$　　//解决“解是什么样的”

附注2——非方阵

（1）$m\times n$矩阵：将$n$维向量变换为$m$维向量　　//$m\neq n$时，基向量的维度发生变化

（2）矩阵的列数表明基向量的个数（输入空间的维数），矩阵的行数表明变换后输出空间的维数

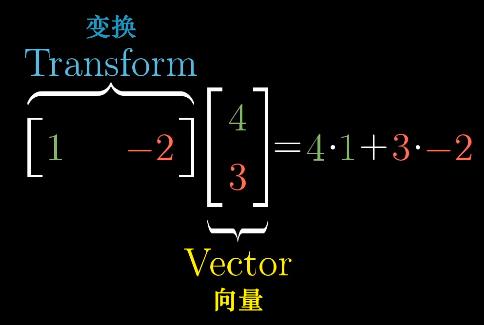
 七、点积与对偶性　　//点积：高维输入，一维输出

（1）$\vec{v}\cdot\vec{w}$标准定义：同维向量对应坐标项相乘后，求和

（2）$\vec{v}\cdot\vec{w}$几何解释：$\vec{v}$在$\vec{w}$方向上的投影长度和$\vec{w}$长度的乘积　　//同向为正，反向为负，垂直为0

注：投影的对称性——点积的结果与顺序无关 $\vec{v}\vec{w}=\vec{w}\vec{v}$

（3）实现“高维输入，一维输出”的线性变换需要满足的直观条件：一系列等距分布于一条直线上的点，应用线性变换后，会保持这些点的等距分布特性；若干输出不是等距分布，则变换不是线性的

 注：一维行向量可以视为高维空间向一维空间的变换矩阵，每个元素可以看作基向量的变换结果，如$\begin{bmatrix}2 & 1\end{bmatrix}$

• 点积与变换的关联：

• 向量与变换之间的关系（直立和放倒）

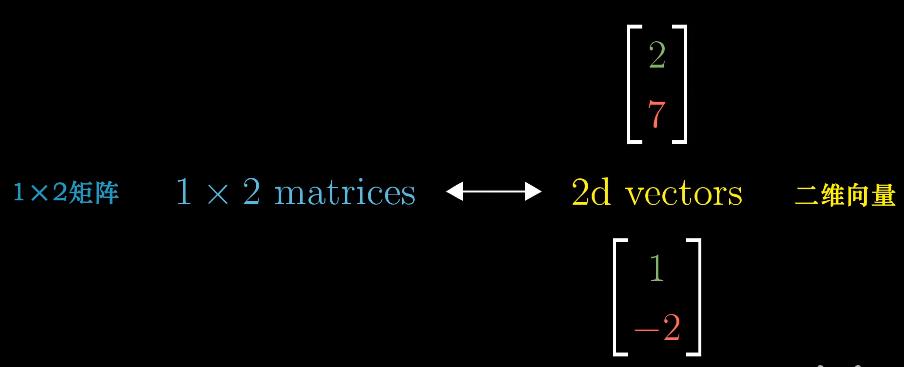
• 投影矩阵projection matrix：二维向量到数的线性变换　　//空间任意向量经过投影变换的结果为投影矩阵与向量相乘

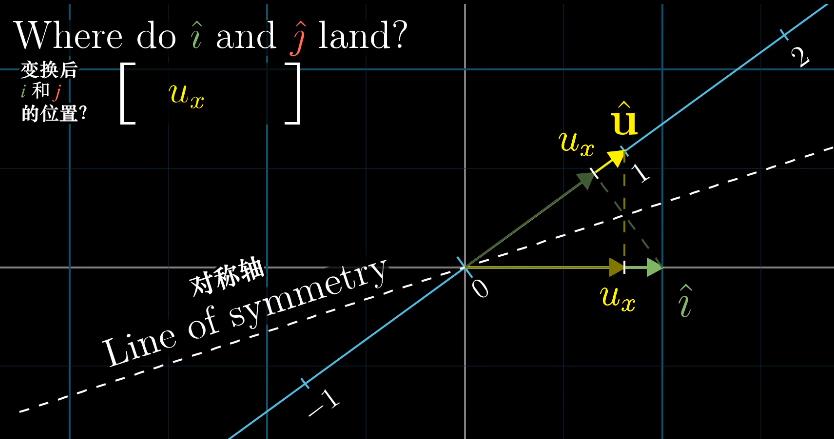
　　如图所示，$\hat{i}$和$\hat{j}$在单位向量$\hat{u}$上的投影值，分别为$u_x$和$u_y$（投影变换矩阵的值）；则投影变换与点积的关系如下：

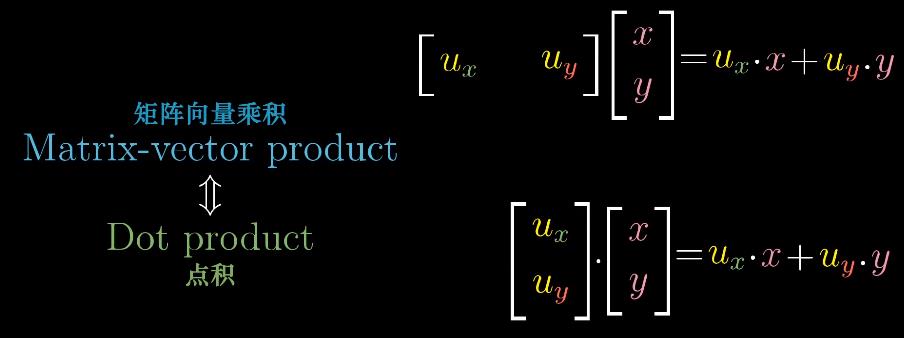
注：任何时候看到一个输出空间为一维数轴的线性变换，空间中会存在唯一的向量$v$与之相关，所以应用变换和与向量$v$做点积是一样的（对偶性duality）

• 向量 $\Leftrightarrow$ 对应的线性变换　　//向量是线性变换的物质载体
• 多维空间到一维空间的线性变换 $\Leftrightarrow$ 多维空间的某个特定向量　　//应用线性变换和与这个向量点乘等价

总结：

• 点积是理解投影的有利几何工具，并便于检验两个向量的指向是否相同
• 两个向量点乘：将其中一个向量转换为线性变换

 八、叉积

1. 标准介绍

（1）二维叉积（等价于行列式）：

$\overrightarrow{v}\times\overrightarrow{w}$ = 构成的平行四边形的面积 * 方向（$\overrightarrow{v}$在$\overrightarrow{w}$右侧为正，否则为负）　　//乘积顺序有影响

注：

• 判断方向的方法，记住横轴单位向量$\hat{i}$与纵轴单位向量$\hat{j}$的叉积$\hat{i}\times\hat{j}$为正　　//基向量的顺序就是定向的基础
• 面积的求法：将向量作为列构成矩阵（与将$\hat{i}$和$\hat{j}$分别移至$\overrightarrow{v}$和$\overrightarrow{w}$的线性变换相对应），矩阵行列式的绝对值即为面积　　//作为行也可以，因为转置不改变行列式的值

（2）三维叉积：通过两个三维向量生成一个新的三维向量    $\overrightarrow{v}\times\overrightarrow{w}=\overrightarrow{p}$

• 生成的三维向量：长度为平行四边形的面积，方向垂直于平行四边形，且符合右手法则

2. 以线性变换的眼光看叉积

（1）线性变换和对偶向量

（2）理解叉积的计算公式和几何含义之间的关系

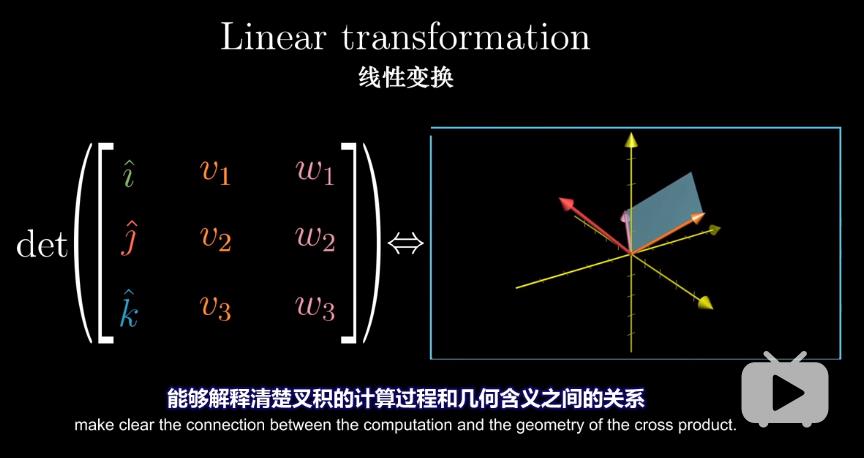
• 定义三维空间到数轴的函数：输入任意向量$(x, y, z)$计算与$\overrightarrow{v}$和$\overrightarrow{w}$确定的平行六面体的体积（考虑方向）

　　注：根据行列式的性质可以证明该函数是线性的

• 寻找对偶向量$\overrightarrow{p}$：线性变换$\Rightarrow$矩阵乘法$\Rightarrow$向量点积

　　注：寻找向量$\overrightarrow{p}$，满足与向量$(x,y,z)$点乘时，所得结果为右侧$3\times 3$矩阵的行列式

$$\Downarrow$$

　　注：计算公式角度

• 向量$\overrightarrow{p}$点积的几何意义：
• 六边体体积计算两种思考方式：

1. 线性函数对于给定向量的作用为：将向量投影到垂直于$\overrightarrow{v}$和$\overrightarrow{w}$的直线上，然后将投影长度与$\overrightarrow{v}$和$\overrightarrow{w}$张成的平行四边形的面积相乘　　//对行列式的解释
2. 等价于：垂直于$\overrightarrow{v}$和$\overrightarrow{w}$且长度为平行四边形面积的向量与向量$(x,y,z)$进行点乘　　//对对偶向量点乘的解释

　　注：几何意义角度

 九、基变换

（1）不同基向量（坐标系）下的坐标表示

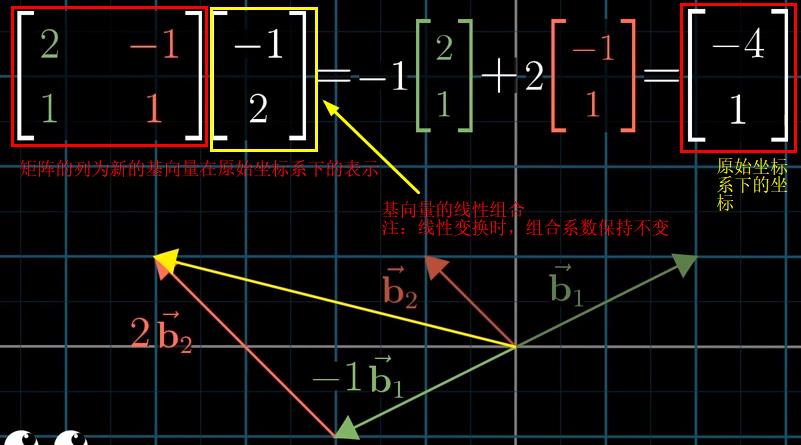
注：当坐标均为$\begin{bmatrix}-1 \\ 2\end{bmatrix}$时，基向量的不同会引起在同一坐标系进行表示时的坐标变化

（2）基变换：矩阵代表基向量的变换

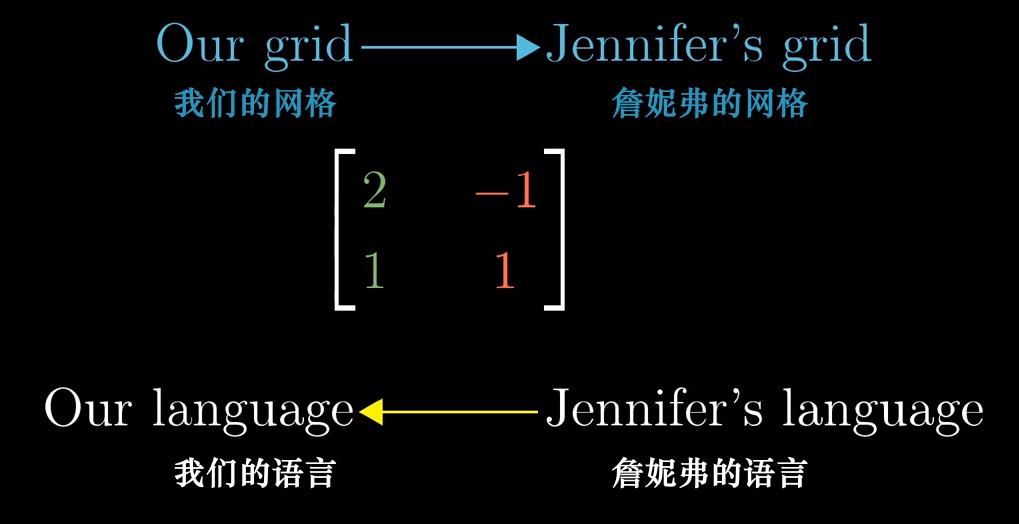
（3）基变换图示

• 基变换矩阵（描述基变量的变化）

• 正变换

• 逆变换

（4）如何利用标准坐标系描述新基下的线性变换

注：先将新基下的向量转化为标准坐标系表示——>在标准坐标系下进行变换——>将坐标重新变换回新基下的坐标

 

注：表达式$\color{red}{A^{-1}MA}$暗示了一种数学上的转移作用，中间的矩阵$M$代表了一种标准坐标系下的常见变换，外侧的两个矩阵则代表着不同坐标系的视角转化（转移作用），相应的矩阵乘积结果仍然代表着同一个变换，但是从其他人（新坐标系）的角度来看的

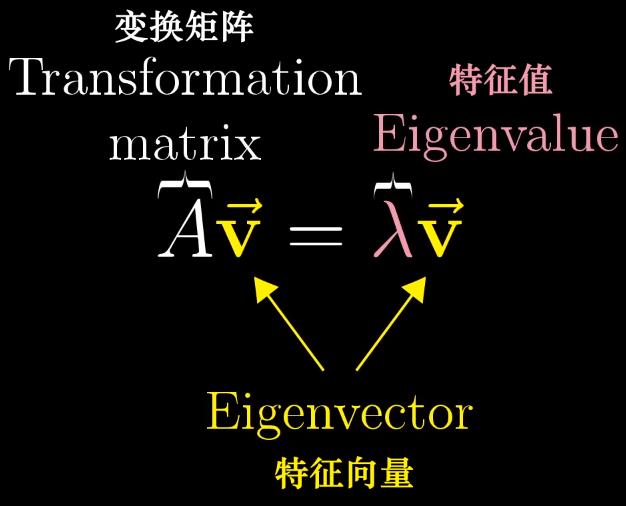
十、特征向量与特征值

（1）特征向量：矩阵变换对它的作用仅仅是拉伸或者压缩，如同一个标量　　//特征向量留在自身张成的空间里（留在直线上，不发生旋转）

（2）特征值：衡量特征向量在变换中拉伸或者压缩比例的因子

（3）对于三维旋转而言，旋转矩阵的特征向量代表了该旋转的旋转轴（不发生变化）　　//旋转矩阵的特征值为1（保持向量长度不变）

（4）理解线性变换作用的两种方式

• 将矩阵列视为变换后的基向量　　//依赖于所选特定坐标系
• 利用特征向量和特征值　　//不依赖于坐标系

（5）求解特征向量、特征值

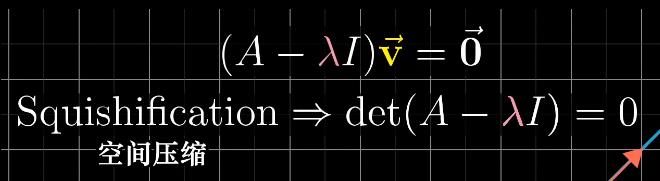
注：当且仅当矩阵$A-\lambda I$代表的变换将空间压缩到更低的维度时，才会存在非零向量$\vec{v}$，使得和矩阵的乘积为零，也就是矩阵的行列式需要为零

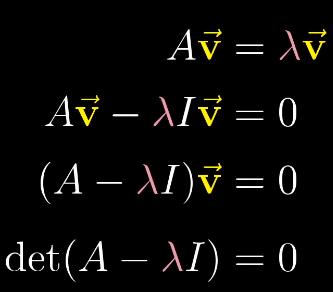
（6）二维线性变换不一定有特征向量：如逆时针旋转90度$\begin{bmatrix}0 & -1 \\ 1 & 0\end{bmatrix}$使得每个向量都发生旋转（离开其张成的空间），此时求解行列式为零得不到实数解，表明没有特征向量

注：与虚数$i$相乘在复平面中表现为90度旋转（与$i$是上述旋转变换的特征值有关联）；特征值出现复数的情况一般对应于变换中的某种旋转

（7）剪切变换矩阵$\begin{bmatrix}1 & 0 \\ 1 & 1\end{bmatrix}$的所有特征向量都位于$x$轴上，特征值为1

注：可能出现只有一个特征值，但是特征向量不止在一条直线上，如$\begin{bmatrix}2 & 0 \\ 0 & 2\end{bmatrix}$的唯一特征值为2，但是平面内每个向量都是特征向量

（8）特征基eigenbasis：一组特征向量作为基向量构成的集合

• 对角矩阵的所有基向量都是特征向量，矩阵的对角元为相应的特征值　　//对角矩阵仅仅让基向量与某个特征值相乘

• 当基向量不是特征向量时，可以通过基变换，将坐标系转换为由特征向量作为基向量（特征向量足够多，能够张成全空间）

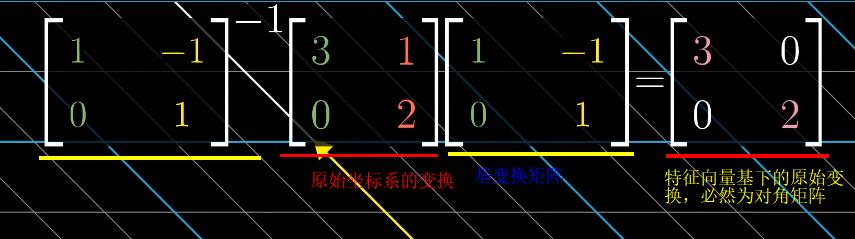
　　注：同一个变换在新基（特征向量）$\begin{bmatrix}1 & 0 \\ -1 & 1\end{bmatrix}$下表示为对角矩阵，且对角线元素为特征值

十一、抽象向量空间　　//类似向量的事物合集，如箭头、一组数、函数等

（1）向量——>函数

• 可加性

• 成比例性

注：可加性和成比例性的直观解释——网格线保持平行且等距分布

• 线性变换（矩阵）和线性算子（求导）之间的对应关系

• 向量空间必须满足的八条公理：

（2）全体多项式空间的基函数basis functions为：$b_0(x)=1, b_1(x)=x, b_2(x)=x^2, b_3(x)=x^3, \cdots$；

对每个基函数求导，并将结果作为矩阵列，可得函数的求导变换矩阵$\frac{d}{dx}$

（3）普适的代价

 

转载于:https://www.cnblogs.com/hg-love-dfc/p/10441586.html