四元数、欧拉角及方向余弦矩阵的相互转换公式
一、欧拉角转四元数(常用来初始化四元数)
按Z-Y-X的旋转变换顺序有:
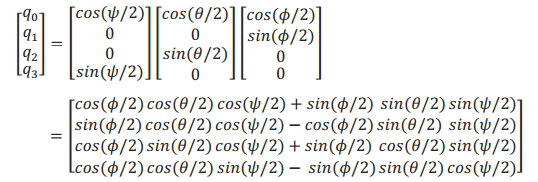
三、欧拉角转方向余弦矩阵
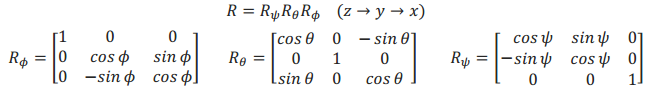 由以上两式可得,经三次基本旋转对应的坐标变换为:
由以上两式可得,经三次基本旋转对应的坐标变换为:
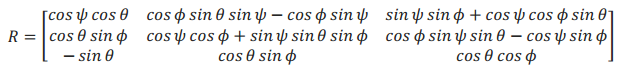 从上述方向余弦矩阵中可方便提取欧拉角
从上述方向余弦矩阵中可方便提取欧拉角
四、四元数转欧拉角
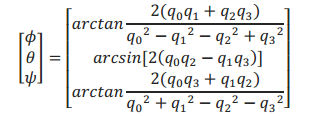
五、附C程序
void eulerAnglesToQuaternion(void)
{
cosRoll = cosf(roll * 0.5f);
sinRoll = sinf(roll * 0.5f);
cosPitch = cosf(pitch * 0.5f);
sinPitch = sinf(pitch * 0.5f);
cosHeading = cosf(hdg * 0.5f);
sinHeading = sinf(hdg * 0.5f);
q0 = cosRoll * cosPitch * cosHeading + sinRoll * sinPitch * sinHeading;
q1 = sinRoll * cosPitch * cosHeading - cosRoll * sinPitch * sinHeading;
q2 = cosRoll * sinPitch * cosHeading + sinRoll * cosPitch * sinHeading;
q3 = cosRoll * cosPitch * sinHeading - sinRoll * sinPitch * cosHeading;
}
void quaternionToRotationMatrix(void)
{
float q1q1 = sq(q1);
float q2q2 = sq(q2);
float q3q3 = sq(q3);
float q0q1 = q0 * q1;
float q0q2 = q0 * q2;
float q0q3 = q0 * q3;
float q1q2 = q1 * q2;
float q1q3 = q1 * q3;
float q2q3 = q2 * q3;
rMat[0][0] = 1.0f - 2.0f * q2q2 - 2.0f * q3q3;
rMat[0][1] = 2.0f * (q1q2 + -q0q3);
rMat[0][2] = 2.0f * (q1q3 - -q0q2);
rMat[1][0] = 2.0f * (q1q2 - -q0q3);
rMat[1][1] = 1.0f - 2.0f * q1q1 - 2.0f * q3q3;
rMat[1][2] = 2.0f * (q2q3 + -q0q1);
rMat[2][0] = 2.0f * (q1q3 + -q0q2);
rMat[2][1] = 2.0f * (q2q3 - -q0q1);
rMat[2][2] = 1.0f - 2.0f * q1q1 - 2.0f * q2q2;
}
void quaternionToEulerAngles(void)
{
roll = atan2f(2.f * (q2q3 + q0q1), q0q0 - q1q1 - q2q2 + q3q3);
pitch = asinf(2.f * (q0q2 - q1q3));
yaw = atan2f(2.f * (q1q2 + q0q3), q0q0 + q1q1 - q2q2 - q3q3);
}
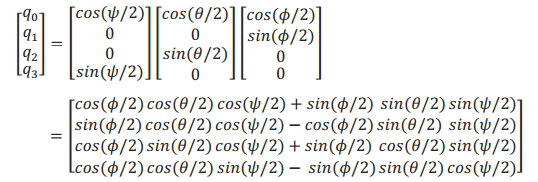
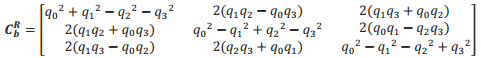
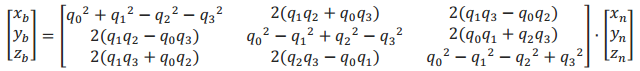
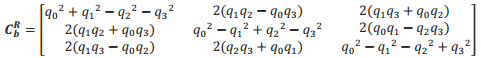
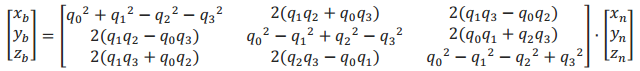
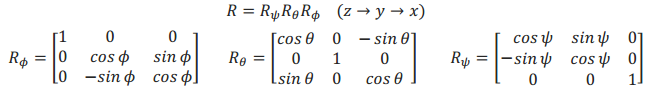
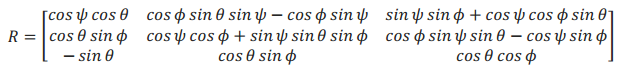
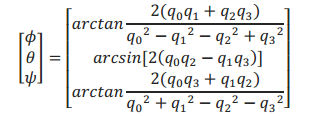







 本文详细介绍了四元数、欧拉角及方向余弦矩阵之间的转换方法,包括欧拉角到四元数、四元数到旋转矩阵、四元数到欧拉角等转换公式,并提供了C语言实现示例。
本文详细介绍了四元数、欧拉角及方向余弦矩阵之间的转换方法,包括欧拉角到四元数、四元数到旋转矩阵、四元数到欧拉角等转换公式,并提供了C语言实现示例。
















 1597
1597

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








