—–下文摘自秦永元的《惯性导航》第二版
设有参考坐标系R ,坐标轴
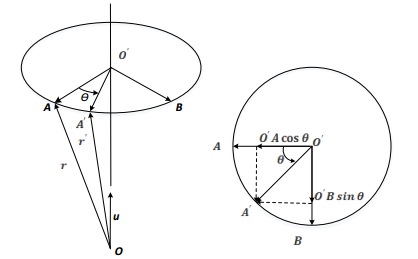
设刚体以ω=ω x i+ω y j+ω z k 相对 R 系旋转,初始时刻位置向量处于
下面分析r 和
OO ′ =(r∙u)u
O ′ A=r−OO ′ =r−(r∙u)u
O ′ B=u×O ′ A=u×r−(r∙u)u=u×r
O ′ A ′ =O ′ Acosθ+O ′ Bsinθ=rcosθ−(r∙u)ucosθ+u×rsinθ
所以
r ′ =OO ′ +O ′ A ′ =rcosθ+(1−cosθ)×(r∙u)u+u×rsinθ
由矢量三重积计算公式:
u×(u×r)=u(u∙r)−(u∙u)r=(r∙u)u−r
即
(r∙u)u=r+u×(u×r)
所以
r ′ =rcosθ+(1−cosθ)[r+u×(u×r)]+u×rsinθ=r+u×rsinθ+(1−cosθ)u×(u×r)
将上式向R 系内投影:
记
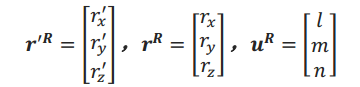
又根据叉乘关系表达式
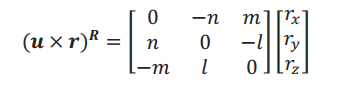
记
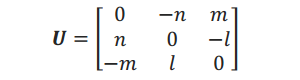
则
(u×r) R =Ur R
[u×(u×r)] R =U∙Ur R
所以
r ′R =r R +Ur R sinθ+(1−cosθ)U∙Ur R =(I+2Usinθ2 cosθ2 +2sin 2 θ2 U∙U)r R
令
D=I+2Usinθ2 cosθ2 +2sin 2 θ2 U∙U
则有:
记初始时刻的刚体固联坐标系为b 0 ,由于初始时刻刚体固联坐标系与参考坐标系重合所以r R =r b 0 而在转动过程中,位置向量和 b 系都同刚体固联,所以位置向量和
r R =r ′R =Dr ′b
该式说明D 即为
即
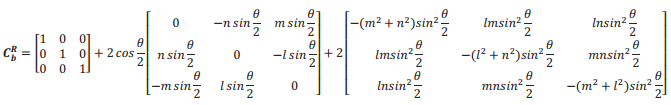
令
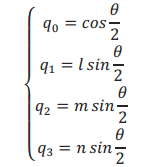
并以q 0 q 1 q 2 q 3 构造四元数:
则可得如下结论:
- 四元数Q=cosθ2 +u R sinθ2 描述了刚体的定点转动,即当只关心b 系相对
R 系的角位置时,可认为b 系是由R 系经过无中间的一次性等效旋转形成的,Q 包含了这种等效旋转的全部信息:u R 为旋转瞬时轴和坐标变换矩阵,θ 为转过的角度。 - 四元数可以确定
b 系至R 系的坐标变换矩阵。
由于‖q‖=q 2 0 +q 2 1 +q 2 2 +q 2 3 =cos 2 θ2 +(l+m+n)sin 2 θ2 =1 ,所以可以进一步推得如下结论:
(1)描述刚体旋转的四元数是规范化四元数。
(2)
(3)如果将向量r R 和r b 看作零标量的四元数,则r R 和r b 间的变换关系可采用四元数乘法表示:r R =Q⊗r b ⊗Q ∗ 该式称为坐标变换的四元数表示法,其中Q 为R 至b 系的旋转四元数。坐标变换的矩阵表示法为:r R =C R b r b








 本文通过解析刚体绕固定点转动的过程,详细介绍了如何利用四元数描述坐标变换,并给出了四元数与坐标变换矩阵之间的转换方法。
本文通过解析刚体绕固定点转动的过程,详细介绍了如何利用四元数描述坐标变换,并给出了四元数与坐标变换矩阵之间的转换方法。
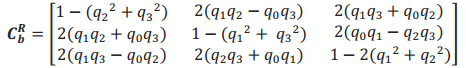
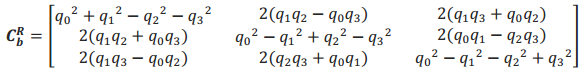
















 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








