求导的定义
求导是数学计算中的一个计算方法,它的定义就是,当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。在一个函数存在导数时,称这个函数可导 或者可微分。可导的函数一定连续。不连续的函数一定不可导。
定义法求导
定义式
f ′ ( x ) = d y d x = lim h → 0 f ( x + h ) − f ( x ) h f'(x)=\frac{dy}{dx}=\lim_{h\to0}\frac{f(x+h)-f(x)}{h} f′(x)=dxdy=h→0limhf(x+h)−f(x)
例一
题目
求 f ( x ) = x f(x)=\sqrt x f(x)=x的导数
解答
f ′ ( x ) = d y d x = lim h → 0 x + h − x h = lim h → 0 ( x + h − x ) ( x + h + x ) h ( x + h + x ) = lim h → 0 x + h − x h ( x + h + x ) = lim h → 0 1 x + h + x = 1 2 x \begin{align} f'(x)=\frac{dy}{dx}&=\lim_{h\to0}\frac{\sqrt{x+h}-\sqrt x}{h}\\ &=\lim_{h\to0}\frac{(\sqrt{x+h}-\sqrt x)(\sqrt{x+h}+\sqrt x)}{h(\sqrt{x+h}+\sqrt x)}\\ &=\lim_{h\to0}\frac{x+h-x}{h(\sqrt{x+h}+\sqrt x)}\\ &=\lim_{h\to0}\frac1{\sqrt{x+h}+\sqrt x}\\ &=\frac 1{2\sqrt x} \end{align} f′(x)=dxdy=h→0limhx+h−x=h→0limh(x+h+x)(x+h−x)(x+h+x)=h→0limh(x+h+x)x+h−x=h→0limx+h+x1=2x1
例二
题目
求 f ( x ) = 1 x f(x)=\frac1x f(x)=x1的导数
解答
f ′ ( x ) = d y d x = lim h → 0 1 x + h − 1 x h = lim h → 0 − h x ( x + h ) h = − lim h → 0 1 x ( x + h ) = − 1 x 2 \begin{align} f'(x)=\frac{dy}{dx}&=\lim_{h\to0}\frac{\frac1{x+h}-\frac1x}{h}\\ &=\lim_{h\to0}\frac{-\frac{h}{x(x+h)}}{h}\\ &=-\lim_{h\to0}\frac1{x(x+h)}\\ &=-\frac1{x^2} \end{align} f′(x)=dxdy=h→0limhx+h1−x1=h→0limh−x(x+h)h=−h→0limx(x+h)1=−x21
多项式求导公式
若 f ( x ) = x a f(x)=x^a f(x)=xa则 f ′ ( x ) = a x a − 1 f'(x)=ax^{a-1} f′(x)=axa−1
求导运算公式求导
和法则
[ f ( x ) + g ( x ) ] ′ = f ( x ) ′ + g ( x ) ′ d y d x = d ( u + v ) d x = d u d x + d v d x [f(x)+g(x)]'=f(x)'+g(x)'\\ \frac{dy}{dx}=\frac{d(u+v)}{dx}=\frac{du}{dx}+\frac{dv}{dx} [f(x)+g(x)]′=f(x)′+g(x)′dxdy=dxd(u+v)=dxdu+dxdv
积法则
[ f ( x ) g ( x ) ] ′ = f ( x ) g ′ ( x ) + f ′ ( x ) g ( x ) d y d x = d ( u v ) d x = u d v d x + v d u d x [f(x)g(x)]'=f(x)g'(x)+f'(x)g(x)\\ \frac{dy}{dx}=\frac{d(uv)}{dx}=u\frac{dv}{dx}+v\frac{du}{dx} [f(x)g(x)]′=f(x)g′(x)+f′(x)g(x)dxdy=dxd(uv)=udxdv+vdxdu
商法则
[ f ( x ) g ( x ) ] ′ = f ′ ( x ) g ( x ) − f ( x ) g ′ ( x ) g 2 ( x ) d y d x = d ( u v ) d x = v d u d x − u d v d x v 2 \Big[\frac{f(x)}{g(x)}\Big]'=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\\ \frac{dy}{dx}=\frac{d(\frac uv)}{dx}=\frac{v\frac{du}{dx}-u\frac{dv}{dx}}{v^2} [g(x)f(x)]′=g2(x)f′(x)g(x)−f(x)g′(x)dxdy=dxd(vu)=v2vdxdu−udxdv
例一
题目
求 f ( x ) = ( x + 1 ) 2 x 2 + 1 f(x)=\frac{(x+1)^2}{x^2+1} f(x)=x2+1(x+1)2的导数
解答
f ( x ) = x 2 + 2 x + 1 x 2 + 1 = 1 + 2 x x 2 + 1 f(x)=\frac{x^2+2x+1}{x^2+1}=1+\frac{2x}{x^2+1} f(x)=x2+1x2+2x+1=1+x2+12x
令 u = 2 x , v = x 2 + 1 u=2x,v=x^2+1 u=2x,v=x2+1
则 d u d x = 2 , d v d x = 2 x \frac{du}{dx}=2,\frac{dv}{dx}=2x dxdu=2,dxdv=2x
用导数运算的商法则
f
′
(
x
)
=
d
y
d
x
=
v
d
u
d
x
−
u
d
v
d
x
v
2
=
2
x
(
x
2
+
1
)
−
2
x
⋅
2
x
(
x
2
+
1
)
2
=
2
x
3
−
4
x
2
+
2
x
x
4
+
2
x
2
+
1
\begin{align} f'(x)=\frac{dy}{dx}&=\frac{v\frac{du}{dx}-u\frac{dv}{dx}}{v^2}\\ &=\frac{2x(x^2+1)-2x\cdot2x}{(x^2+1)^2}\\ &=\frac{2x^3-4x^2+2x}{x^4+2x^2+1}\\ \end{align}
f′(x)=dxdy=v2vdxdu−udxdv=(x2+1)22x(x2+1)−2x⋅2x=x4+2x2+12x3−4x2+2x
三角函数的导数(一)
两个重要的极限
lim h → 0 sin x x = 1 lim h → 0 cos x − 1 x = 0 \lim_{h\to0}\frac {\sin x} x=1\qquad\lim_{h\to0}\frac{\cos x-1}{x}=0 h→0limxsinx=1h→0limxcosx−1=0
基础三角函数的导数
正弦函数的导数
sin ′ ( x ) = d y d x = lim h → 0 sin ( x + h ) − sin ( x ) h = lim h → 0 sin ( x ) cos ( h ) + cos ( x ) sin ( h ) − sin ( x ) h = lim h → 0 sin ( x ) [ cos ( h ) − 1 ] + cos ( x ) sin ( h ) h = lim h → 0 sin ( x ) ⋅ cos ( h ) − 1 h + cos ( x ) sin ( h ) h = cos ( x ) \begin{align} \sin'(x)=\frac{dy}{dx}&= \lim_{h\to0}\frac{\sin(x+h)-\sin(x)}{h}\\ &=\lim_{h\to0}\frac{\sin(x)\cos(h)+\cos(x)\sin(h)-\sin(x)}{h}\\ &=\lim_{h\to0}\frac{\sin(x)[\cos(h)-1]+\cos(x)\sin(h)}{h}\\ &=\lim_{h\to0}\sin(x)\cdot\frac{\cos(h)-1}{h}+\cos(x)\frac{\sin(h)}{h}\\ &=\cos(x) \end{align} sin′(x)=dxdy=h→0limhsin(x+h)−sin(x)=h→0limhsin(x)cos(h)+cos(x)sin(h)−sin(x)=h→0limhsin(x)[cos(h)−1]+cos(x)sin(h)=h→0limsin(x)⋅hcos(h)−1+cos(x)hsin(h)=cos(x)
余弦函数的导数
cos ′ ( x ) = d y d x = lim h → 0 cos ( x + h ) − cos ( x ) h = lim h → 0 cos ( x ) cos ( h ) − sin ( x ) sin ( h ) − cos ( x ) h = lim h → 0 cos ( x ) [ cos ( h ) − 1 ] − sin ( x ) sin ( h ) h = lim h → 0 cos ( x ) ⋅ cos ( h ) − 1 h − sin ( x ) sin ( h ) h = − sin ( x ) \begin{align}\cos'(x)=\frac{dy}{dx}&=\lim_{h\to0}\frac{\cos(x+h)-\cos(x)}{h}\\&=\lim_{h\to0}\frac{\cos(x)\cos(h)-\sin(x)\sin(h)-\cos(x)}{h}\\&=\lim_{h\to0}\frac{\cos(x)[\cos(h)-1]-\sin(x)\sin(h)}{h}\\ &=\lim_{h\to0}\cos(x)\cdot\frac{\cos(h)-1}{h}-\sin(x)\frac{\sin(h)}{h}\\&=-\sin(x)\end{align} cos′(x)=dxdy=h→0limhcos(x+h)−cos(x)=h→0limhcos(x)cos(h)−sin(x)sin(h)−cos(x)=h→0limhcos(x)[cos(h)−1]−sin(x)sin(h)=h→0limcos(x)⋅hcos(h)−1−sin(x)hsin(h)=−sin(x)
正切函数的导数
令
u
=
sin
(
x
)
,
v
=
cos
(
x
)
u=\sin(x),v=\cos(x)
u=sin(x),v=cos(x),则
d
u
d
x
=
cos
(
x
)
,
d
v
d
x
=
−
sin
(
x
)
\frac{du}{dx}=\cos(x),\frac{dv}{dx}=-\sin(x)
dxdu=cos(x),dxdv=−sin(x)
tan
′
(
x
)
=
(
u
v
)
′
=
v
d
u
d
x
−
u
d
v
d
x
v
2
=
cos
2
(
x
)
+
sin
2
(
x
)
cos
2
(
x
)
=
1
cos
2
(
x
)
=
sec
2
(
x
)
\begin{align} \tan'(x)=\Big(\frac{u}{v}\Big)'&=\frac{v\frac{du}{dx}-u\frac{dv}{dx}}{v^2}\\ &=\frac{\cos^2(x)+\sin^2(x)}{\cos^2(x)}\\ &=\frac1{\cos^2(x)}\\ &=\sec^2(x) \end{align}
tan′(x)=(vu)′=v2vdxdu−udxdv=cos2(x)cos2(x)+sin2(x)=cos2(x)1=sec2(x)
余切函数的导数
令
u
=
cos
(
x
)
,
v
=
sin
(
x
)
u=\cos(x),v=\sin(x)
u=cos(x),v=sin(x),则
d
u
d
x
=
−
sin
(
x
)
,
d
v
d
x
=
cos
(
x
)
,
\frac{du}{dx}=-\sin(x),\frac{dv}{dx}=\cos(x),
dxdu=−sin(x),dxdv=cos(x),
cot
′
(
x
)
=
(
u
v
)
′
=
v
d
u
d
x
−
u
d
v
d
x
v
2
=
−
sin
2
(
x
)
−
cos
2
(
x
)
sin
2
(
x
)
=
−
1
sin
2
(
x
)
=
−
csc
2
(
x
)
\begin{align} \cot'(x)=\Big(\frac{u}{v}\Big)'&=\frac{v\frac{du}{dx}-u\frac{dv}{dx}}{v^2}\\ &=\frac{-\sin^2(x)-\cos^2(x)}{\sin^2(x)}\\ &=-\frac1{\sin^2(x)}\\ &=-\csc^2(x) \end{align}
cot′(x)=(vu)′=v2vdxdu−udxdv=sin2(x)−sin2(x)−cos2(x)=−sin2(x)1=−csc2(x)
正割函数的导数
令
u
=
cos
x
u=\cos x
u=cosx,则
d
u
d
x
=
−
sin
(
x
)
,
d
y
d
u
=
−
1
u
2
\frac{du}{dx}=-\sin(x),\frac{dy}{du}=-\frac{1}{u^2}
dxdu=−sin(x),dudy=−u21
sec
′
(
x
)
=
d
y
d
x
=
d
y
d
u
⋅
d
u
d
x
=
sin
(
x
)
cos
2
(
x
)
=
tan
(
x
)
sec
(
x
)
\sec'(x)=\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}=\frac{\sin(x)}{\cos^2(x)}=\tan(x)\sec(x)
sec′(x)=dxdy=dudy⋅dxdu=cos2(x)sin(x)=tan(x)sec(x)
余割函数的导数
令
u
=
sin
x
u=\sin x
u=sinx,则
d
u
d
x
=
cos
(
x
)
,
d
y
d
u
=
−
1
u
2
\frac{du}{dx}=\cos(x),\frac{dy}{du}=-\frac{1}{u^2}
dxdu=cos(x),dudy=−u21
csc
′
(
x
)
=
d
y
d
x
=
d
y
d
u
⋅
d
u
d
x
=
−
cos
(
x
)
sin
2
(
x
)
=
cot
(
x
)
csc
(
x
)
\csc'(x)=\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}=-\frac{\cos(x)}{\sin^2(x)}=\cot(x)\csc(x)
csc′(x)=dxdy=dudy⋅dxdu=−sin2(x)cos(x)=cot(x)csc(x)
例一
题目
求 f ( x ) = x sin ( 5 x ) f(x)=x\sin(5x) f(x)=xsin(5x)的导数
解答
令 U = x , V = sin ( 5 x ) U=x,V=\sin(5x) U=x,V=sin(5x)
令
u
=
5
x
u=5x
u=5x则
d
u
d
x
=
5
,
d
V
d
u
=
−
cos
(
u
)
\frac{du}{dx}=5,\frac{dV}{du}=-\cos(u)
dxdu=5,dudV=−cos(u)
d
V
d
x
=
d
V
d
u
⋅
d
u
d
x
=
−
5
cos
(
5
x
)
\frac{dV}{dx}=\frac{dV}{du}\cdot\frac{du}{dx}=-5\cos(5x)
dxdV=dudV⋅dxdu=−5cos(5x)
因为
d
U
d
x
=
1
,
d
V
d
x
=
−
5
cos
(
5
x
)
\frac{dU}{dx}=1,\frac{dV}{dx}=-5\cos(5x)
dxdU=1,dxdV=−5cos(5x)
f
′
(
x
)
=
U
d
V
d
x
+
V
d
U
d
x
=
−
5
x
cos
(
5
x
)
+
sin
(
5
x
)
f'(x)=U\frac{dV}{dx}+V\frac{dU}{dx}=-5x\cos(5x)+\sin(5x)
f′(x)=UdxdV+VdxdU=−5xcos(5x)+sin(5x)
指数函数与对数函数的导数
e e e的定义
假设你在一家银行里存钱,若一笔存在银行里的时间为一年的 1 n \frac 1n n1,你将获得本金 1 n \frac 1n n1的利息,很明显你一钱存越多次能获得的利息越多(假设你每次存钱),但这是无上限的吗?很显然是不可能的。
我们可以列表
| n n n | 1 1 1 | 2 2 2 | 3 3 3 | 4 4 4 | ⋯ \cdots ⋯ | 100 100 100 | ⋯ \cdots ⋯ | 1 0 4 10^4 104 |
|---|---|---|---|---|---|---|---|---|
| 连本利率 | 2 2 2 | 2.25 2.25 2.25 | 2.37 2.37 2.37 | 2.4414 2.4414 2.4414 | ⋯ \cdots ⋯ | 2.704813 2.704813 2.704813 | ⋯ \cdots ⋯ | 2.7181459 2.7181459 2.7181459 |
当你的 n n n足够大时,连本利率的增长速度变得极为缓慢(从 100 100 100增长到 1 0 4 10^4 104,连本利率只增加了 0.013 0.013 0.013左右),它因该收敛与某个常数。
这样我们引出了自然常数 e e e,它定义为 e = lim n → ∞ ( 1 + 1 n ) n e=\lim_{n\to\infty}(1+\frac1n)^n e=limn→∞(1+n1)n,它约等于 2.718281 2.718281 2.718281,我们待会会说明为什么被称为自然常数。
指数函数的导数
我们先求 f ( x ) = a x f(x)=a^x f(x)=ax的导数
用导数的定义式来求
f
′
(
x
)
=
d
y
d
x
=
lim
h
→
0
a
x
+
h
−
a
x
h
=
lim
h
→
0
a
x
(
a
h
−
1
)
h
=
a
x
lim
h
→
0
a
h
−
1
h
\begin{align} f'(x)=\frac{dy}{dx}&=\lim_{h\to 0}\frac{a^{x+h}-a^x}{h}\\ &=\lim_{h\to 0}\frac{a^x(a^h-1)}{h}\\ &=a^x\lim_{h\to0}\frac{a^h-1}{h}\\ \end{align}
f′(x)=dxdy=h→0limhax+h−ax=h→0limhax(ah−1)=axh→0limhah−1
令
t
=
a
h
−
1
t=a^h-1
t=ah−1则
h
=
log
a
t
+
1
h=\log_a{t+1}
h=logat+1,当
lim
h
→
0
t
=
0
\lim_{h\to0}t=0
limh→0t=0得
f
′
(
x
)
=
a
x
lim
t
→
0
t
log
a
t
+
1
=
a
x
lim
t
→
0
1
log
a
(
1
+
t
)
1
t
=
a
x
1
log
a
e
=
a
x
ln
a
ln
e
=
a
x
ln
a
\begin{align} f'(x)&=a^x\lim_{t\to0}\frac{t}{\log_at+1}\\ &=a^x\lim_{t\to0}\frac{1}{\log_a(1+t)^{\frac1t}}\\ &=a^x\frac{1}{\log_ae}\\ &=a^x\frac{\ln a}{\ln e}\\ &=a^x\ln a \end{align}
f′(x)=axt→0limlogat+1t=axt→0limloga(1+t)t11=axlogae1=axlnelna=axlna
对数函数的导数
我们讨论 f ( x ) = log a x f(x)=\log_ax f(x)=logax的导数
用导数的定义式来求
$$
\begin{align}
f’(x)=\frac{dy}{dx}&=\lim_{h\to0}\frac{\log_a(x+h)-\log_ax}{h}\
&=\lim_{h\to0}\frac{\log_a(1+\frac h x)}{h}\
&=\lim_{h\to 0}\log_a(1+\frac hx)^{\frac{1}{h}}\
&=\lim_{h\to 0}\frac 1x\log_a(1+\frac hx)^{\frac xh}\
\end{align}
KaTeX parse error: Can't use function '$' in math mode at position 3: 令$̲t=\frac xh$,当$\…
\begin{align}
f’(x)&=\lim_{t\to\infty}\frac1x\log(1+\frac1t)^t\
&=\frac1x\log_ae\
&=\frac1x\cdot\frac{\ln e}{\ln a}=\frac{1}{x\ln a}
\end{align}
$$
隐函数求导
隐函数的定义
如果方程 f ( x , y ) = 0 f(x,y)=0 f(x,y)=0能确定 y y y是 x x x的函数,那么称这种方式表示的函数是隐函数。而函数就是指:在某一变化过程中,两个变量 x x x、 y y y,对于某一范围内的 x x x的每一个值, y y y都有确定的值和它对应, y y y就是 x x x的函数。这种关系一般用 y = f ( x ) y=f(x) y=f(x)即显函数来表示。 f ( x , y ) = 0 f(x,y)=0 f(x,y)=0即隐函数是相对于显函数来说的。
隐函数的求导方法
我们可以举出一个相当经典的隐函数 x 2 + y 2 = 1 x^2+y^2=1 x2+y2=1
我们尝试求出它在点 ( x , y ) (x,y) (x,y)点的切线斜率 d y d x \frac{dy}{dx} dxdy
首先我们把 x x x和 y y y放在等号两边得 x 2 − 1 = − y 2 x^2-1=-y^2 x2−1=−y2
我们对两边同时求导左边是相当方便的,可得 ( x 2 − 1 ) ′ = 2 x (x^2-1)'=2x (x2−1)′=2x
但我们对右边求导时出现了问题我们要求的是 d y d x \frac{dy}{dx} dxdy但我们的变化量为 d y dy dy
我们可使用链式求导法则 d ( − y 2 ) d y d y d x = − 2 y d y d x \frac{d(-y^2)}{dy}\frac{dy}{dx}=-2y\frac{dy}{dx} dyd(−y2)dxdy=−2ydxdy
整理后为 2 x = − 2 y d y d x 2x=-2y\frac{dy}{dx} 2x=−2ydxdy即 d y d x = − x y \frac{dy}{dx}=-\frac xy dxdy=−yx。
通过两边同时对 x x x求导我们便解决了隐函数的求导问题
例一
题目
f : e x y 3 − x 2 + 2 y = 1 f:e^xy^3-x^2+2y=1 f:exy3−x2+2y=1,求 d y d x \frac{dy}{dx} dxdy, d 2 y d x 2 \frac {d^2y}{dx^2} dx2d2y
解答
求 d y d x \frac{dy}{dx} dxdy,我们先对 x x x求导,得 e x y 3 + e x 3 y 2 d y d x − 2 x + 2 d y d x = 0 e^xy^3+e^x3y^2\frac{dy}{dx}-2x+2\frac{dy}{dx}=0 exy3+ex3y2dxdy−2x+2dxdy=0
可得 d y d x = 2 x − e x y 3 3 e x y 2 + 2 \frac{dy}{dx}=\frac{2x-e^xy^3}{3e^xy^2+2} dxdy=3exy2+22x−exy3
求 d 2 y d x 2 \frac{d^2y}{dx^2} dx2d2y,对 e x y 3 + e x 3 y 2 d y d x − 2 x + 2 d y d x = 0 e^xy^3+e^x3y^2\frac{dy}{dx}-2x+2\frac{dy}{dx}=0 exy3+ex3y2dxdy−2x+2dxdy=0再次对 x x x求导
得 e x y 3 + 3 e x y 2 d y d x + 3 e x y 2 d y d x + 6 e x y ( d y d x ) 2 + 3 e x y 2 d 2 y d x 2 − 2 + 2 d 2 y d x 2 = 0 e^xy^3+3e^xy^2\frac{dy}{dx}+3e^xy^2\frac{dy}{dx}+6e^xy(\frac{dy}{dx})^2+3e^xy^2\frac{d^2y}{dx^2}-2+2\frac{d^2y}{dx^2}=0 exy3+3exy2dxdy+3exy2dxdy+6exy(dxdy)2+3exy2dx2d2y−2+2dx2d2y=0
则 d 2 y d x 2 = 2 − e x y 3 − 6 e x y 2 d y d x + 6 e x y ( d y d x 2 ) 3 e x y 2 + 2 \frac{d^2y}{dx^2}=\frac{2-e^xy^3-6e^xy^2\frac{dy}{dx}+6e^xy(\frac{dy}{dx}^2)}{3e^xy^2+2} dx2d2y=3exy2+22−exy3−6exy2dxdy+6exy(dxdy2),其中 d y d x = 2 x − e x y 3 3 e x y 2 + 2 \frac{dy}{dx}=\frac{2x-e^xy^3}{3e^xy^2+2} dxdy=3exy2+22x−exy3
三角函数求导(二)
反三角函数的导数
反正弦函数的导数
因为 y = arcsin ( x ) y=\arcsin(x) y=arcsin(x),所以 x = sin ( y ) x=\sin(y) x=sin(y)
我们对 x = sin ( y ) x=\sin(y) x=sin(y)关于 x x x进行隐函数求导,得 1 = cos ( y ) d y d x 1=\cos(y)\frac{dy}{dx} 1=cos(y)dxdy
因为 x = sin ( y ) x=\sin(y) x=sin(y),所以 cos ( y ) = ± 1 − x 2 \cos(y)=\pm\sqrt{1-x^2} cos(y)=±1−x2。
所以 d y d x = ± 1 1 − x 2 \frac{dy}{dx}=\pm\frac{1}{\sqrt{1-x^2}} dxdy=±1−x21中的一个。我们可以分析 y = arcsin ( x ) y=\arcsin(x) y=arcsin(x)的图像
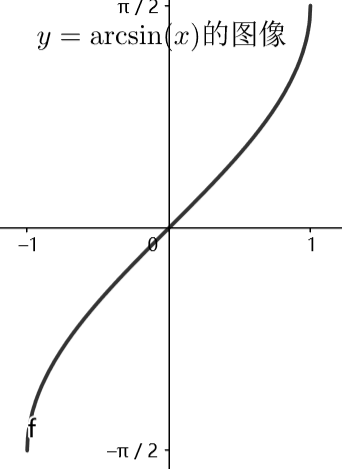
容易发现 y = arcsin ( x ) y=\arcsin(x) y=arcsin(x)是导数恒为正的增函数,所以 d y d x = 1 1 − x 2 \frac{dy}{dx}=\frac{1}{\sqrt{1-x^2}} dxdy=1−x21
反余弦函数的导数
因为 y = arccos ( x ) y=\arccos(x) y=arccos(x),所以 x = cos ( y ) x=\cos(y) x=cos(y)
我们对 x = cos ( y ) x=\cos(y) x=cos(y)关于 x x x进行隐函数求导,得 1 = − sin ( y ) d y d x 1=-\sin(y)\frac{dy}{dx} 1=−sin(y)dxdy
因为 x = cos ( y ) x=\cos(y) x=cos(y),所以 sin ( y ) = ± 1 − x 2 \sin(y)=\pm\sqrt{1-x^2} sin(y)=±1−x2。
所以 d y d x = ± 1 1 − x 2 \frac{dy}{dx}=\pm\frac{1}{\sqrt{1-x^2}} dxdy=±1−x21中的一个。我们可以分析 y = arccos ( x ) y=\arccos(x) y=arccos(x)的图像
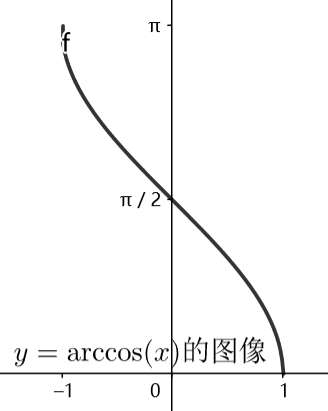
容易发现 y = arccos ( x ) y=\arccos(x) y=arccos(x)是导数恒为负的减函数,所以 d y d x = − 1 1 − x 2 \frac{dy}{dx}=-\frac{1}{\sqrt{1-x^2}} dxdy=−1−x21
反正切/余切函数的导数
因为 y = arctan ( x ) y=\arctan(x) y=arctan(x),所以 x = tan ( y ) x=\tan(y) x=tan(y)
我们对 x = tan ( y ) x=\tan(y) x=tan(y)关于 x x x隐函数求导得 d y d x = 1 sec 2 ( y ) = 1 x 2 + 1 \frac{dy}{dx}=\frac{1}{\sec^2(y)}=\frac{1}{x^2+1} dxdy=sec2(y)1=x2+11
同理 y = cot − 1 ( x ) y=\cot^{-1}(x) y=cot−1(x),所以 x = cot ( y ) x=\cot(y) x=cot(y)
我们对 x = cot ( y ) x=\cot(y) x=cot(y)关于 x x x隐函数求导,得 d y d x = − 1 csc 2 ( y ) = − 1 1 + x 2 \frac{dy}{dx}=-\frac{1}{\csc^2(y)}=-\frac{1}{1+x^2} dxdy=−csc2(y)1=−1+x21
反正割/余割函数的导数
我们与上面做法相同,由 y = sec − 1 ( x ) y=\sec^{-1}(x) y=sec−1(x),所以 x = sec ( y ) x=\sec(y) x=sec(y)
我们对 x = sec ( y ) x=\sec(y) x=sec(y)对于 x x x隐函数求导得 d y d x = 1 sec ( y ) tan ( y ) = 1 ± x x 2 − 1 \frac{dy}{dx}=\frac{1}{\sec(y)\tan(y)}=\frac{1}{\pm x\sqrt{x^2-1}} dxdy=sec(y)tan(y)1=±xx2−11
又出现了考虑正负的情况,我们可以分析图像
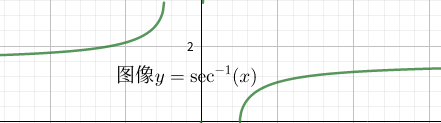
发现它是恒正的,可得 sec − 1 ( x ) ′ = 1 ∣ x ∣ x 2 − 1 \sec^{-1}(x)'=\frac{1}{|x|\sqrt{x^2-1}} sec−1(x)′=∣x∣x2−11
同理可得 csc − 1 ( x ) ′ = − 1 ∣ x ∣ x 2 − 1 \csc^{-1}(x)'=-\frac{1}{|x|\sqrt{x^2-1}} csc−1(x)′=−∣x∣x2−11
双曲函数的导数
我们只粗略的讲双曲函数,因为他实际上是指数函数的求导,所以十分简单,我们放在最后讲
双曲正弦/余弦函数的导数
sinh ( x ) ′ = ( e x − e − x 2 ) ′ = e x + e − x 2 = cosh ( x ) cosh ( x ) ′ = ( e x + e − x 2 ) ′ = e x − e − x 2 = sin ( x ) \sinh(x)'=\Big(\frac{e^x-e^{-x}}{2}\Big)'=\frac{e^x+e^{-x}}{2}=\cosh(x)\\ \cosh(x)'=\Big(\frac{e^x+e^{-x}}{2}\Big)'=\frac{e^x-e^{-x}}{2}=\sin(x) sinh(x)′=(2ex−e−x)′=2ex+e−x=cosh(x)cosh(x)′=(2ex+e−x)′=2ex−e−x=sin(x)
其它双曲函数的导数
和三角函数一样的,我们可以通过
sinh
\sinh
sinh和
cosh
\cosh
cosh来定义其它双曲函数,结论如下,你可以自己推出来。
tanh
(
x
)
′
=
1
cos
2
(
x
)
,
coth
(
x
)
=
−
1
sinh
2
(
x
)
\tanh(x)'=\frac{1}{\cos^2(x)},\coth(x)=-\frac{1}{\sinh^2(x)}
tanh(x)′=cos2(x)1,coth(x)=−sinh2(x)1
























 1286
1286











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








