原文链接:https://dreamhomes.github.io/posts/202101041501.html
文章链接:https://arxiv.org/abs/1904.10098
源码链接:https://github.com/fishmoon1234/DAG-GNN
TL;DR
论文中提出一种新的DAG编码架构 DAG-GNN,其实模型的本质就是一个图变分自编码器,模型的优点是既能处理连续型变量又能处理离散型变量;在人工数据集和真实数据集中验证了模型结果可以达到全局最优 🤔;
Model / Algorithm
论文中的整体模型架构如下:
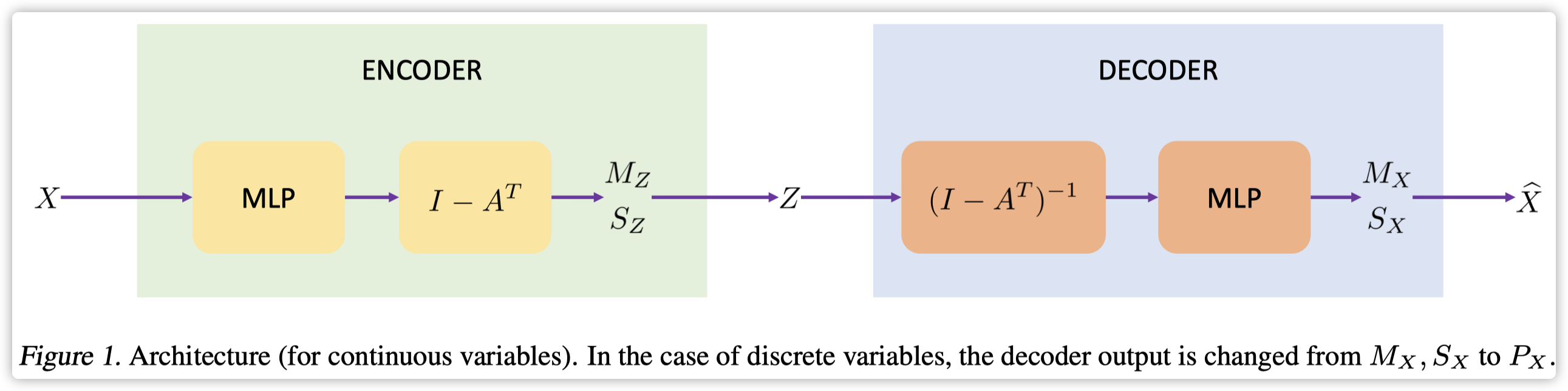
Linear Structural Equation Model
论文中首先通过生成模型来泛化线性结构等价模型;假设
A
∈
R
m
×
m
A \in \mathbb{R}^{m \times m}
A∈Rm×m 表示DAG的加权邻接矩阵,
X
∈
R
m
×
d
X \in \mathbb{R}^{m \times d}
X∈Rm×d 表示每个节点的特征,那么线性模型的的编码方式为:
X
=
A
T
X
+
Z
(
1
)
X=A^{T} X+Z \quad\quad\quad(1)
X=ATX+Z(1)
其中
Z
∈
R
m
×
d
Z \in \mathbb{R}^{m \times d}
Z∈Rm×d 表示噪声矩阵;如果图中节点是以拓扑序排列的,那么矩阵
A
A
A 是一个严格的上三角矩阵,因此DAG中的 ancestral sampling 等价于三角等式的解:
X
=
(
I
−
A
T
)
−
1
Z
(
2
)
X=\left(I-A^{T}\right)^{-1} Z \quad\quad\quad(2)
X=(I−AT)−1Z(2)
Proposed Graph Neural Network Model
上述等式 (2) 可以写为
X
=
f
A
(
Z
)
X=f_A(Z)
X=fA(Z),可以表示为数据节点特征
Z
Z
Z 并得到embedding
X
X
X。传统的GCN 架构计算公式如下:
X
=
A
^
⋅
ReLU
(
A
^
Z
W
1
)
⋅
W
2
X=\widehat{A} \cdot \operatorname{ReLU}\left(\widehat{A} Z W^{1}\right) \cdot W^{2}
X=A
⋅ReLU(A
ZW1)⋅W2
由于公式 (2) 的特殊结构,因此提出新的图神经网络架构,注意这是解码器的结构:
X
=
f
2
(
(
I
−
A
T
)
−
1
f
1
(
Z
)
)
(
3
)
X=f_{2}\left(\left(I-A^{T}\right)^{-1} f_{1}(Z)\right)\quad\quad\quad(3)
X=f2((I−AT)−1f1(Z))(3)
其中 f 1 , f 2 f_1, f_2 f1,f2 表示 Z , X Z, X Z,X 的非线性的转换函数;
Model Learning with Variational Autoencoder
对于给定的分布
Z
Z
Z 和样本
X
1
,
⋯
,
X
n
X^1, \cdots, X^n
X1,⋯,Xn,生成模型的目标是最大化对数函数:
1
n
∑
k
=
1
n
log
p
(
X
k
)
=
1
n
∑
k
=
1
n
log
∫
p
(
X
k
∣
Z
)
p
(
Z
)
d
Z
\frac{1}{n} \sum_{k=1}^{n} \log p\left(X^{k}\right)=\frac{1}{n} \sum_{k=1}^{n} \log \int p\left(X^{k} \mid Z\right) p(Z) d Z
n1k=1∑nlogp(Xk)=n1k=1∑nlog∫p(Xk∣Z)p(Z)dZ
由于上式难以解决因此使用变分贝叶斯;
使用变分后验概率
q
(
Z
∣
X
)
q(Z|X)
q(Z∣X) 来近似实际后验概率
q
(
Z
∣
X
)
q(Z|X)
q(Z∣X)。网络优化的结果是 ELBO(the evidence lower bound)
L
E
L
B
O
=
1
n
∑
k
=
1
n
L
E
L
B
O
k
L_{\mathrm{ELBO}}=\frac{1}{n} \sum_{k=1}^{n} L_{\mathrm{ELBO}}^{k}
LELBO=n1k=1∑nLELBOk
其中
L
E
L
B
O
k
≡
−
D
K
L
(
q
(
Z
∣
X
k
)
∥
p
(
Z
)
)
+
E
q
(
Z
∣
X
k
)
[
log
p
(
X
k
∣
Z
)
]
\begin{array}{r} L_{\mathrm{ELBO}}^{k} \equiv-D_{\mathrm{KL}}\left(q\left(Z \mid X^{k}\right) \| p(Z)\right) \\ \quad+\mathrm{E}_{q\left(Z \mid X^{k}\right)}\left[\log p\left(X^{k} \mid Z\right)\right] \end{array}
LELBOk≡−DKL(q(Z∣Xk)∥p(Z))+Eq(Z∣Xk)[logp(Xk∣Z)]
基于 (3)式的解码器结构,对应的编码器结构为
Z
=
f
4
(
(
I
−
A
T
)
f
3
(
X
)
)
(
5
)
Z=f_{4}\left(\left(I-A^{T}\right) f_{3}(X)\right) \quad\quad\quad(5)
Z=f4((I−AT)f3(X))(5)
其中
f
4
,
f
3
f_4, f_3
f4,f3 表示
f
2
,
f
1
f_2,f_1
f2,f1 的逆函数。
Loss Function
对于编码器,使用MLP表示
f
3
f_3
f3和恒等映射表示
f
4
f_4
f4,变分后验概率
q
(
Z
∣
X
)
q(Z|X)
q(Z∣X) 是一个因子高斯分布均值
M
Z
∈
R
m
×
d
M_Z\in \mathbb{R}^{m\times d}
MZ∈Rm×d 标准差
S
Z
∈
R
m
×
d
S_Z\in \mathbb{R}^{m\times d}
SZ∈Rm×d,可以通过编码器来进行计算:
[
M
Z
∣
log
S
Z
]
=
(
I
−
A
T
)
MLP
(
X
,
W
1
,
W
2
)
(
6
)
\left[M_{Z} \mid \log S_{Z}\right]=\left(I-A^{T}\right) \operatorname{MLP}\left(X, W^{1}, W^{2}\right)\quad\quad\quad(6)
[MZ∣logSZ]=(I−AT)MLP(X,W1,W2)(6)
其中
MLP
(
X
,
W
1
,
W
2
)
:
=
ReLU
(
X
W
1
)
W
2
\operatorname{MLP}\left(X, W^{1}, W^{2}\right):=\operatorname{ReLU}\left(X W^{1}\right) W^{2}
MLP(X,W1,W2):=ReLU(XW1)W2。
对于生成模型,使用恒等映射表示
f
1
f_1
f1 MLP来表示
f
2
f_2
f2,得到的似然
p
(
X
∣
Z
)
p(X | Z)
p(X∣Z) 符合高斯分布均值为
M
X
∈
R
m
×
d
M_X\in \mathbb{R}^{m\times d}
MX∈Rm×d 标准差为
S
X
∈
R
m
×
d
S_X\in \mathbb{R}^{m\times d}
SX∈Rm×d,解码器的计算公式如下:
[
M
X
∣
log
S
X
]
=
MLP
(
(
I
−
A
T
)
−
1
Z
,
W
3
,
W
4
)
(
7
)
\left[M_{X} \mid \log S_{X}\right]=\operatorname{MLP}\left(\left(I-A^{T}\right)^{-1} Z, W^{3}, W^{4}\right)\quad\quad\quad(7)
[MX∣logSX]=MLP((I−AT)−1Z,W3,W4)(7)
基于公式(6)(7),式(4)中的KL散度项为:
D
K
L
(
q
(
Z
∣
X
)
∥
p
(
Z
)
)
=
1
2
∑
i
=
1
m
∑
j
=
1
d
(
S
Z
)
i
j
2
+
(
M
Z
)
i
j
2
−
2
log
(
S
Z
)
i
j
−
1
\begin{array}{l} D_{\mathrm{KL}}(q(Z \mid X) \| p(Z))= \\\\ \quad \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{d}\left(S_{Z}\right)_{i j}^{2}+\left(M_{Z}\right)_{i j}^{2}-2 \log \left(S_{Z}\right)_{i j}-1 \end{array}
DKL(q(Z∣X)∥p(Z))=21∑i=1m∑j=1d(SZ)ij2+(MZ)ij2−2log(SZ)ij−1
重构准确率项为:
E
q
(
Z
∣
X
)
[
log
p
(
X
∣
Z
)
]
≈
1
L
∑
l
=
1
L
∑
i
=
1
m
∑
j
=
1
d
−
(
X
i
j
−
(
M
X
(
l
)
)
i
j
)
2
2
(
S
X
(
l
)
)
i
j
2
−
log
(
S
X
(
l
)
)
i
j
−
c
\begin{array}{c} \mathrm{E}_{q(Z \mid X)}[\log p(X \mid Z)] \approx \\\\ \frac{1}{L} \sum_{l=1}^{L} \sum_{i=1}^{m} \sum_{j=1}^{d}-\frac{\left(X_{i j}-\left(M_{X}^{(l)}\right)_{i j}\right)^{2}}{2\left(S_{X}^{(l)}\right)_{i j}^{2}}-\log \left(S_{X}^{(l)}\right)_{i j}-c \end{array}
Eq(Z∣X)[logp(X∣Z)]≈L1∑l=1L∑i=1m∑j=1d−2(SX(l))ij2(Xij−(MX(l))ij)2−log(SX(l))ij−c
对于不同类型变量的处理论文中使用了不同的结构,详细参考原文推导过程。
Experiments
人工数据集
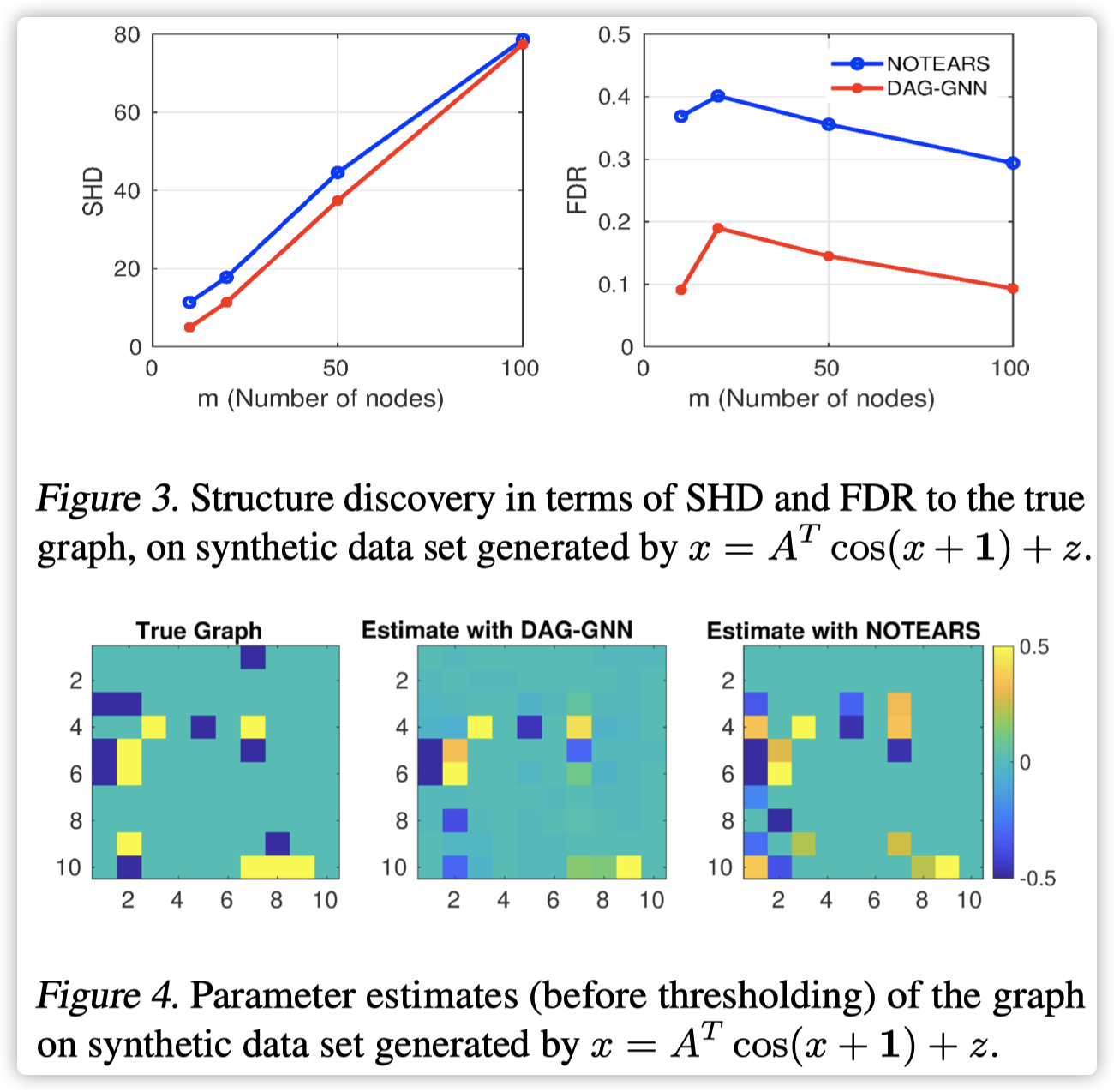
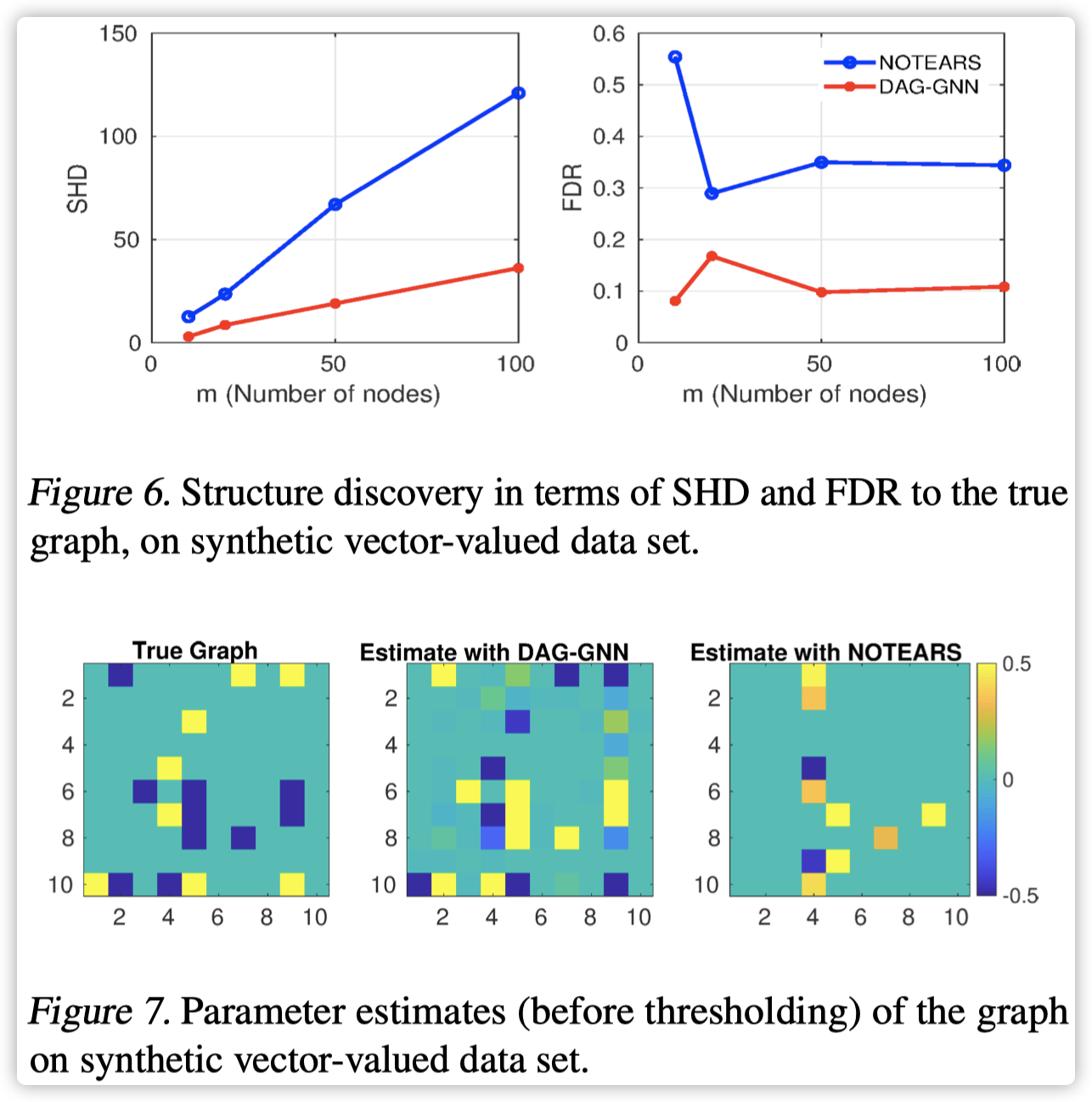






















 2803
2803











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








