《FEDLION: FASTER ADAPTIVE FEDERATED OPTIMIZATION WITH FEWER COMMUNICATION》论文解读

摘要

在联邦学习中，常用的FedAvg框架往往收敛速度较慢，导致训练过程中通讯成本较高的问题。为解决这挑战，我们引入FedLion自适应联邦优化算法，将集中式自适应算法Lion集成到联邦学习中。此外，由于在本地训练中使用了符号梯度下降，与现有的自适应算法相比，FedLion降低了通讯期间的数据传输要求，进一步降低了通讯成本。同时，FedLion比FedAvg更快收敛。

介绍

联邦学习

联邦学习作为一种保护隐私的分布式框架，即许多客户端协作训练机器学习模型，同时通过不相互共享或与中央服务器共享来保护其本地数据。取而代之的是，客户端仅与中央服务器进行交互，以交换模型参数或梯度。我们的主要关注点集中在一个集中式参数服务器和 N 个客户端的场景上，我们的目标是解决以下分布式优化问题：

$\underset{x\in \mathbb{R}}{\min }f(x)=\frac{1}{N}\sum _{i=1}^N{f}_i(x)$ （1）

其中$f_i(\cdot )$表示客户端本地目标函数。
在设计分布式算法来解决（1）中问题时，首要考虑的是通讯效率问题，因为大量客户端需要频繁地讲本地的模型/参数传输到中央参数服务器。最著名的FedAvg算法采用多次局部梯度下降，并定期进行通讯来减少通讯开销。

联邦学习中的自适应优化器

在集中式的神经网络训练中，自适应的优化算法，利用历史梯度信息来增强后续优化迭代。典型的具有动量的随机梯度下降算法（SGD）、Adam，联邦学习也引入自适应技术来达到加速收敛的效果，然后现有的算法有一个共同点，在链路传输中都需要比常用的FedAvg算法多两到三倍的比特，这是因为它们在传输过程中出了本地模型/参数外，还需要传输辅助变量，如本地本地动量或控制变量。

本文提到的自适应联邦优化算法FedLion将集中式自适应算法Lion集成到联邦学习中，无论是理论上还是实际中，他只需要比FedAvg多传输较多一点的比特，就能实现更快的收敛速度。

自适应的Lion优化联邦算法

模型和动量的周期平均法

伪代码：
$T$:通讯论述
$E$:本地epochs
$\gamma$:学习率
$({\beta }_1,{\beta }_2)$:动量系数
$B$:batchsize
$n$:每轮参与训练的客户端数
1、初始化全局模型$x_0$和全局0元素动量$m_0$
2、每轮通讯
客户端：
随机选取$n$个客户端进行采样(其中$n$<$N$(总客户端数))
2.1、每个客户端
如第$i$个客户端接收全局模型$x_{t-1}$并赋值为$x_{t-1}^i$；接收全局动量$m_{t-1}$并赋值$m_{t-1}^i$
2.1.1、每个客户端每轮本地训练
计算以batchsize为$B$的本地梯度$g_{t-1,s}^i$，
$h_{t-1}^i,s$引入动量系数${\beta }_1$和符号函数的动量来计算第 { t − 1 } \{t-1\} {t−1}次通讯中第$i$个客户端在第$s$轮次的梯度下降，
$x_{t-1,s}^i$由第 { t − 1 } \{t-1\} {t−1}通讯中第$i$个客户端在第$s$轮次更新全局模型$x_{t-1,s-1}$得到
$m_{t-1,s}^i$由第 { t − 1 } \{t-1\} {t−1}通讯中第$i$个客户端在第$s$轮次引入动量系数${\beta }_2$更新全局动量$m_{t-1,s-1}^i$得到
3、结束本地训练
参数${\Delta }_{t-1}^i$由第 { t − 1 } \{t-1\} {t−1}通讯的全局模型$x_{t-1}$减去经过本地训练的第 { t − 1 } \{t-1\} {t−1}通讯$E$epochs第$i$个客户端本地训练后得到的$x_{t-1,E}^i$本地模型的结果除以学习率$\gamma$得到的参数
发送参数${\Delta }_{t-1}^i$和更新后的动量$m_{t-1,E}^i$给服务器端
4、服务器：
$x_t$表示全局模型$x_{t-1}$将参与第 { t − 1 } \{t-1\} {t−1}次通讯的所有客户端参数进行聚合更新的全局模型
$m_t$表示全局动量$m_{t-1}$将第 { t − 1 } \{t-1\} {t−1}次通讯的所有客户端
先前的研究工作可将集中式自适应算法（如SGD和Adam）扩展到联邦学习范式中：定期聚合本地模型和本地辅助变量（如动量）。我们在Algorithm 1：FedLion中将Lion集成进联邦学习范式中。 其中我们在Algorithm 1：FedLion的第15步中：
${\Delta }_{t-1}^i=(x_{t-1}-x_{(t-1),E}^i/\gamma )=\sum _{s=1}^E{h}_{(t-1,s^{\cdot })}^i$

由于符号操作，意味着${\Delta }_{t-1}^i$需要在$[-E,E]$中取整数，这代表需要不超过的$\log (2E-1)$比特。因此，这种方法在通讯过程中显著的减少了传输比特，因为每个客户端只需要传输一个整数值向量和一个全精度向量，而FAFED和FedDA中需要传输两个或三个全精度向量。

收敛分析

对于任意向量$v\in {\mathbb{R}}^d$,$v(j)$表示$v$的第$j$个元素。

Assumption 1.

A.1 小批量梯度是无偏且有界方差，$\mathbb{E}[g_i(x)]=\nabla f_i(x)$（无偏）
并且$\mathbb{E}[|g_i(x)(j)-\nabla f_i(x)(y){|}^2]\le {\sigma }_j^2,\forall j.$（有界）

无偏

无偏样本方差：$S^2=\frac{1}{n-1}{\sum }_{i=1}^n(X_i-\bar{X}{)}^2$
有偏样本方差：$S^2=\frac{1}{n}{\sum }_{i=1}^n(X_i-\bar{X}{)}^2$
两者的区别就是一个除以的是n-1,而另一个除以的是n。这里的n或n-1称之为自由度。自由度通俗的理解就是比如一个数值列表list=[x1,x2,x3]，如果我们此时知道list的平均值为2，那么对于x1,x2变量我们可以任取，若x1=1,x2=2,那么要使list均值为2那么x3只能取3，此时x3就不再是自变量。那么在平均值已知的条件下，能自由取值的变量就只有2个而不是3个。所以此时list的自由度为2。同理，对于样本方差公式中用到了 $\bar{X}$，所以在平均值$\bar{X}$已知的情况下自由度就是n-1而不是n。
总结的结论就是：在样本量较小的时候，无偏方差更符合实际的总体方差，当样本量较大时，无偏方差和有偏方差区别不大。总的说来用无偏样本方差来估计总体方差会更加准确。
参考：https://zhuanlan.zhihu.com/p/157799814

A.2 每个$f_i$是平滑的，即对于任意的$x,y\in {\mathbb{R}}^d$,存在部分非负常数$L_1,L_2,....,L_d$使得$|\nabla f(y)(j)-\nabla f(x)(j)|\le L_j,\forall j.$

A.3 $f$是具有下界，即存在常数$f^{\ast }$使得$f(x)\ge f^{\ast },\forall x\in {\mathbb{R}}^d$

A.4 存在一个常数$\alpha \le \frac{1}{3}$，使得$||\nabla f(x)-\nabla f_i(x)|{|}_1\le \alpha ||\nabla f(x)|{|}_1,\forall x,i.$

Assumption 1中A.1-A.3是先前研究中常用的假设，尤其是在分析基于符号的优化算法时。在算法中提出假设A.4，目的是约束局部目标函数内的异质性。
A.4与现有的有界异质性相比具有稍强的约束，如对比以下A.5
A.5 $||\nabla f(x)-\nabla f_i(x)|{|}_2\le \delta ,\forall i,x.$
这表明我们提出的算法特别适用于具有中等异质性的场景。此外，与FedAvg等现有算法相比，减少异质性的权衡导致了更高的收敛率，正如Theorem 1中的结果所证实的那样。尽管Algorithm 1 局限于 A.4 所特有的设置，但实证观察突出了它在两个最普遍的联合基准上的出色表现，从而强调了它的实际效用。

Theorem 1

假设Assumption 1中A.1-4成立。${\bar{x}}_{t,s}=\frac{1}{N}{\sum }_{i=1}^N{x}_{t,s}^i,\bar{L}={\sum }_{j=1}^d{L}_j$ 和 $\bar{\sigma }={\sum }_{j=1}^d{\sigma }_j$，如果我们设置学习率$\gamma =\frac{1}{\sqrt{T}},{\beta }_1=1-\frac{1}{\sqrt{T}},{\beta }_2=1-\frac{1}{T}$,对于Algorithm 1，存在三个常数$C_1,C_2,C_3$,使得
$\frac{1}{TE}\sum _{t=1,...,T}\sum _{s=1,...,E}\mathbb{E}[||\nabla f({\bar{x}}_{t-1,s-1})|{|}_1]\le \frac{1}{1-3\alpha }(\frac{f(x_0)-f^{\ast }}{E\sqrt{T}}+\frac{c_1\bar{L}}{\sqrt{T}}+\frac{c_2\bar{\sigma }}{\sqrt{nT}}+\frac{c_3\bar{L}E}{\sqrt{T}}).(2)$
综上所述，参数$E$取决于问题的几何特征。具体来说，涉及到平衡（2）中首项和尾项的的贡献。例如，通过设置$E$类似$(f(x_0)-f^{\ast }/C_3\bar{L}{)}^{\frac{1}{2}}=O(1).(3)$,我们实现了函数梯度的$l_1$范数$O(T^{-\frac{1}{2}})$的收敛率。相反，如果我们设置$E=O(T^{-\frac{1}{4}})$，这是FedAvg算法中的设置，我们就能达到(3)中的收敛效果。
$(\frac{1}{TE}\sum _{t,s}\mathbb{E}[||\nabla f({\bar{x}}_{t-1,s-1})|{|}_1]{)}^2\le O(T^{-\frac{1}{2}}).(3)$
通过观察(3)中的收敛边界，函数梯度平方的$l_1$范数以$O(T^{-\frac{1}{2}})$速率收敛。在某些情况下，该速率可以超过FedAvg的$O((nT{)}^{-\frac{1}{2}})$。具体来说，$||v|{|}_2\le ||v|{|}_1$适用于任何向量$v\in {\mathbb{R}}^d$。此外 ，如果梯度足够密集，即$\frac{||v|{|}_1}{||v|{|}_2}\gg n^{\frac{1}{4}}$，我们提出的算法可以比以$l_2$范数平方的$O((nT{)}^{-\frac{1}{2}})$收敛速率快得多。

实验

设置

数据集：CIFAR_10和EMNIST
EMNIST：
客户端：3579
每一轮通讯中，随机选择100个客户端传输梯度参数。
CIFAR-10：
客户端：100
训练样本分布在客户端之间，。每一个客户端的标签上都具有多项式分布。每个客户端都拥有从参数为 1 的对称Dirichlet分布派生的标签上的多项式分布。在每一轮通讯中，100 个客户中有 10 个被统一抽样参与。对于网络架构，我们对 EMNIST 数据集采用 2 层 CNN，对 CIFAR-10 采用Group Normalization的ResNet18。
在比较分析基线FedAvg和其他三种自适应的联邦学习算法：MFL、FedDA、FAFED。
超参数：从集合 { 0.1 , 0.01 , 0.001 } \{0.1,0.01,0.001\} {0.1,0.01,0.001}中选择作为FedAvg、MFL 和 FAFED的最佳学习率。同时保留MFL和FAFED的的默认超参数，即一阶和二阶动量系数为0.9和0.99。对于FedDA，我们采用FedDA和SGDwM版本，并使用与其原始实验设置相同的超参数。我们在 所有实验中为 FedLion 设置了 $\gamma =0.001,{\beta }_1=0.9和{\beta }_2=0.99$。

Dirichlet相关概念

二项分布（Binomial Distribution）

进行$n$次独立随机试验，出现结果$1$的概率是$p$，如果用随机变量$X$表示结果$1$出现的次数，那么：
$P(X=m)=\left(\begin{array}{c}n\\ m\end{array}\right)p^m(1-p{)}^{n-m},m=0,1,2,...,n.$
如果$n=1$，那么二项分布等同于伯努利分布（Bernoulli Distribution）。

多项式分布（Multinomial Distribution）

下面将二项拓展到多想。进行$n$次独立随机实验，每次实验结果有$k$中，其中第$i$种出现的概率为$p_i$，第$i$种出翔的次数为$n_i$，如果随机变量 X = { X 1 , X 2 , . . . , X k } X=\{X_1,X_2,...,X_k\} X={X1​,X2​,...,Xk​}表示实验的所有可能结果的次数，那么：
$P(X_1=n_1,X_2=n_2,...,X_k=n_k)=\frac{n!}{n_1!n_2!...n_k!}{p}_1^{n_1}{p}_2^{n_2}...p_k^{n_k}=\frac{n!}{{\prod }_{i=1}^k}\prod _{i=1}^k{p}_i^{n_i}$
记作$X\backsim Mult(n,p)$。
如果$n=1$，那么多项分布等同于类别分布（Categorical Distribution）。可以看出，二项分布是多项分布的特殊情况，而伯努利分布式类别分布的特殊情况。

狄利克雷分布（Dirichlet Distribution）

下面我们再扩展到多元连续随机变量。狄利克雷分布是贝塔分布的扩展。定义多元连续随机变量 θ = { θ 1 , θ 2 , . . . , θ k } \theta=\{\theta_1,\theta_2,...,\theta_k\} θ={θ1​,θ2​,...,θk​}的概率密度函数为
$p(\theta |\alpha )=\frac{\Gamma ({\sum }_{i=1}^k{\alpha }_i)}{{\prod }_{i=1}^k\Gamma ({\alpha }_i)}\prod _{i=1}^k{\theta }_i^{{\alpha }_i-1},{\alpha }_i>0,i=1,2,...,k.$
其中${\sum }_{i=1}^k{\theta }_i=1,{\theta }_i\ge 0$，则称随机变量$\theta$服从参数为$\alpha$的狄利克雷分布，记作$\theta \backsim Dir(\alpha )$。
定义为$B(\alpha )\stackrel{△}{=}\frac{{\prod }_{i=1}^k\Gamma ({\alpha }_i)}{\Gamma ({\sum }_{i=1}^k{\alpha }_i)}$
那么狄利克雷分布的概率密度甘薯可以表示为$p(\theta |\alpha )=\frac{1}{B(\alpha )}\prod _{i=1}^k{\theta }_i^{{\alpha }_i-1}$
$B(\alpha )$又称为多元贝塔函数或则扩展贝塔函数，其积分表示为
$B(\alpha )=\int \prod _{i=1}^k{\theta }_i^{{\alpha }_i-1}d\theta$
参考：https://blog.csdn.net/philthinker/article/details/111999552

结果

首先，我们将参数$E$从 5 增加到 20 时，由于包含了更多的局部步骤，所有算法都表现出加速的性能。FedLion 始终优于所有现有的自适应算法， 从而在所研究的两个数据集中确立了自己作为自适应算法中最先进的新技术。

图为EMNIST 和 CIFAR-10 数据集的实验结果。前两行代表从EMNIST获得的结果，而后面的两行是CIFAR-10的结果。奇数行表示训练损失曲线，偶数行表示测试精度曲线。对于所有数字，X轴表示通信轮次。从左到右排列的列显示以 E = { 5 , 10 , 20 } E=\{5,10,20\} E={5,10,20} 的不同值获得的结果。

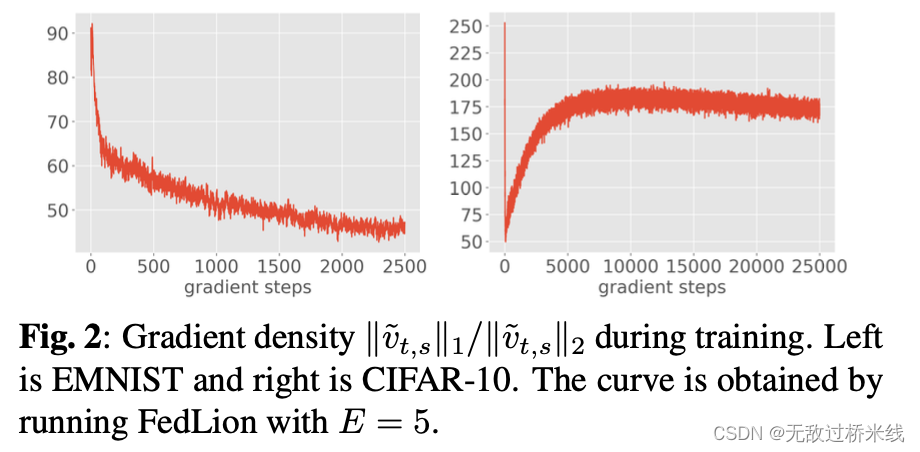
梯度密度

综上所述，FedLion在处理密集梯度时表现出更快的收敛性，并且优于主要优化$L_2$范数收敛的现有算法。为了证实我们在神经网络实践训练中重新计算梯度密度的经验观察结果，我们引入两个变量${\tilde{v}}_{t,s}=\frac{1}{n}{\sum }_{i=1}^n{g}_{t-1,s}^i$和$v_{t,s}=\nabla f({\bar{x}}_{t-1,s-1}).$在图中我们通过检查训练过程中小批量梯度的密度$||{\tilde{v}}_{t,s}|{|}_1/||{\tilde{v}}_{t,s}|{|}_2$ 来证明。图中清晰的证明了在实际场景中，梯度趋于密集(大于$n^{\frac{1}{4}}$ )，FedLion算法提供了更快加速收敛。

上行链路通信的内在量化

我们发现上行链路通信期间${\Delta }_{t-1}^i$的每个元素都可以用最大$\log (2E+1)$比特来表示。我们对${\Delta }_{t-1}^i$值的分布进行了实证研究，考虑了各种设置 E ∈ { 5 , 10 , 20 } E\in\{5,10,20\} E∈{5,10,20}并将结果置于以下图中。在 EMNIST 数据集中，我们观察到值往往聚集 在下限和中限附近。这表明使用高效的编码技术，在实际场景中使用明显少于理论要求的 l位$\log (2E+1)$来表 示${\Delta }_{t-1}^i$是可行的。在 CIFAR-10 数据集中也观察到类似的趋势，尽管与 EMNIST 数据集相比，分布更均匀，但是可能需要更高的位数。

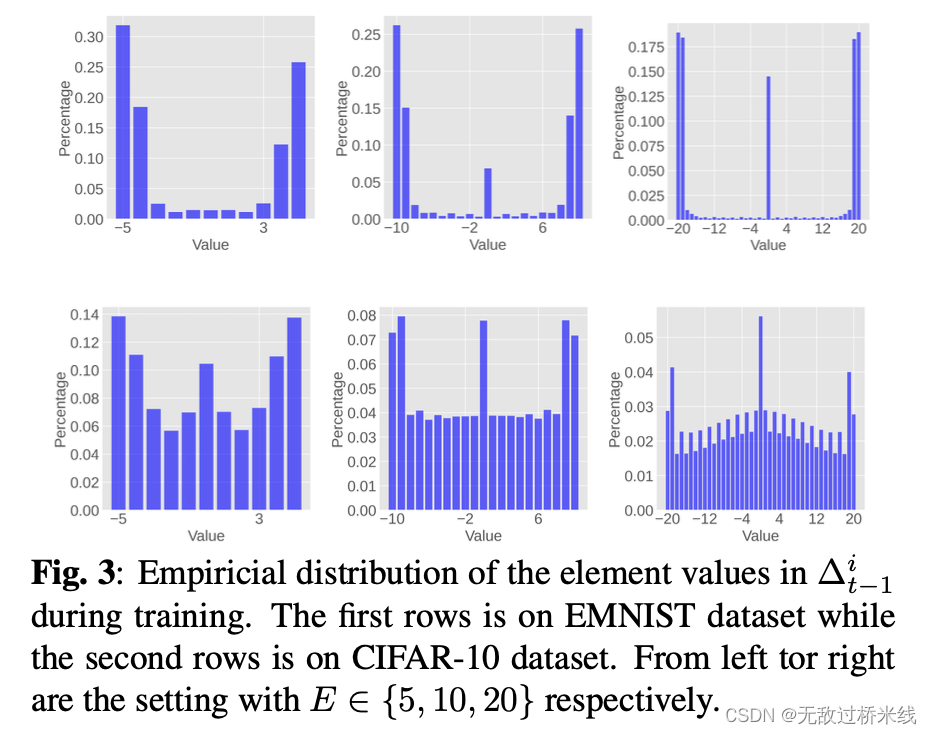
Empiricial distribution

经验分布函数（Empirical Distribution Function，EDF）是一种非参数的分布估计方法。它通过对数据样本的累积分布函数进行估计来逼近未知分布函数。经验分布函数具有一致性和渐近正态性等重要性质，并可用于构建置信区间和进行假设检验。

CONCLUSION

本文提出一种新型的自适应联邦优化算法FedLion算法，继承了Lion（一种最先进的中心化算法）进联邦学习中。FedLion 实现了卓越的理论收敛率，特别是在具有密集梯度的场景中。实证评估表明，FedLion 的收敛速度很快，优于以前的先进算法，如 FAFED 和 FedDA，同时与 FedAvg 相比，上行链路传输位仅略有增加。

后续我会将自己对这篇论文的理解不断更新…

论文链接：https://arxiv.org/pdf/2402.09941v1
代码：https://github.com/tzw1998/fedlion