姿态结算相关----梯度下降法

前一章说到了姿态的表示和最常用的三个传感器，有了原始数据之后就要表示姿态(转换矩阵)啊，转换矩阵有误差咋整？想办法修正啊，修正的目的就是让误差趋近于零。

本章所介绍的梯度下降法都是读博主yzhajlydy博文的理解，图文多引用该博主的博文“四元数姿态的梯度下降法推导和解读”。但是本文很多内容都是我自己码的！！！

梯度下降法让误差趋近于零的方法就是沿着(误差函数)梯度的反方向走一定的步长，迭代操作下去最终就会达到最小误差。先来说说什么是梯度，“标量场中某一点的梯度指向在这点标量场增长最快的方向（当然要比较的话必须固定方向的长度），梯度的绝对值是长度为1的方向中函数最大的增加率，也就是说 ，其中  代表方向导数。”wikipedia如是说。

那根据定义我们定义一个误差函数ef(x)，那么我们的工作就是令ef(x)=0，他的自变量x=[q0 q1 q2 q3]。这也就是说， 原先的标量函数ef(q) 变成了如今的标量函数 ef([q0 q1q2 q3]) ，他仍然是标量函数，但是自变量是向量[q0 q1 q2q3]。

对上述自变量是向量的标量函数，我们要用梯度法求解，就必须求导。标量函数对向量求导很简单，只需要分别对向量中的各个变量求偏导即可：

但是，我们的姿态解算是三维姿态，不是一维姿态，所以，这里的ef(q)实质上是一个向量函数 ef(q)，这个向量函数里面有三个元素，分别对应xyz轴的三个分量，每个分量都由四元数向量 q 构成。那么现在就引入了一个较为复杂的误差函数 ef(q)，该误差函数不光自变量是一个向量，并且因变量也是一个向量，这种函数叫做 多元向量函数 。那么我们现在的问题就转化为 求多元向量函数的极值问题，对多元向量函数求导，就是求 雅可比矩阵（Jacobian） 。定四元数向量 q为行向量，三轴分量[efx、efy、efz]为列向量，则jacobian矩阵如下：

    

wikipedia给出梯度下降法计算公式：

从上述公式也可以看出梯度下降法属于一阶收敛，对于上述公式的理解，就是在 处的梯度（导数），前面的负号表示梯度的反方向，这个方向就是当前最快的下降收敛速度，我们按照这个方向走步长  ，就从  走到了  。在这里，我们取函数  的方向，即  。

根据前述讨论，这里的函数就是误差函数，并且是多元向量函数，自变量是四元数向量，因变量是三维坐标。这里先讨论只利用加速度计表征的四元数矩阵误差，所以该多元向量误差函数记作

上述公式其实就是重力加速度g={0, 0,1}在地理坐标系中的值通过N2B矩阵转换到机体坐标系B中，也就是旋转矩阵的第三列，然后减去当前加速度计测得的值作差，就是通过加速度计表征的旋转矩阵的误差。很显然，这个误差函数就是典型的多元向量函数，当这个函数等于0时，我们就认为得到了旋转矩阵没有误差，也就是姿态四元数是精确的，从而得到了飞行器的精确姿态。根据前述阐述，上述函数的导数就是其对应的雅可比矩阵(3x4)：

到这里，还没有应用到梯度下降算法，只是做好了前提准备。为了更好的理解梯度算法的原理，这里从标量函数梯度开始看起。设标量函数f(x)，导数有f’(x)，对于x上的一个增量dx，有dy=f’(x)dx。当dy->0时，我们认为已经到达稳定解，梯度法计算完成。同理，x变为向量四元数  ，y变为三维向量，那么f’(x)变为雅可比矩阵  ，有梯度计算公式：

至于为什么对jacobian矩阵进行转置，大家自己想想矩阵乘法吧。结果得到的梯度是一个(4x3)X(3x1)=4X1的列向量：

根据梯度下降法的计算公式，假设我们经过梯度下降法计算的目标姿态为  ，那么有：

上述公式就是根据梯度下降算法求得的一组四元数，对梯度归一化得到梯度的方向，其梯度大小由步长ut决定。这样的一个迭代公式显然属于一阶线性收敛，通过计算机的迭代运算可以从初始时刻的姿态每一步经由梯度的相反方向走到多元向量误差函数的一个局部极值点，这个点就是我们消除了旋转矩阵误差的点，就是我们所要求的姿态四元数。

根据madgwick在内部报告《An efficientorientation filter for inertial andinertial/magneticsensor arrays》中，步长

步长ut和实际物体运动的角速度相关，和采样时间相关。

那现在我们基于加速计根据梯度下降法得到了一组四元数。但是我说了我们的主要元件是陀螺仪，姿态结算主要是利用陀螺仪由四元数微分方程完成的。好了手上有了两组四元数，那就对他们融合呗，最简单的方法--加权求和。假设由微分方程求解的姿态四元数为 qw,t ，有：

此式中用于高速运动，用于低速运动，这很好理解，我们之前说了，陀螺仪检测的是角速度，高速运动时可信，加速计在静止或匀速运动时检测的是重力加速度的分量，这时可以直接根据加速计输出来算倾角。

式中存在一个很明显的问题，即 系数 α如何取 ？很明显，高速运动下α要小一些，低速运动下α要大一些。也就是说 理论上将这应该是一个动态变化的值 。至于这个动态值应该怎么取舍就交给那些大牛们去研究吧，我这里就采用常量简单处理了。在常量值处理的前提下，上述公式取得最优值的α应该是  的收敛速度等于  的收敛速度，所以就有如下公式：

式中的β就是四元数微分方程求解的姿态算法的收敛速度，这个值就是陀螺仪的测量误差，通过查询IMU器件的PDF手册就可以知道，一般是一个很小的值。等式右边  就是梯度下降算法的收敛速度，进而有：

 

在分析上述公式之前，首先要明确一点就是梯度下降算法的收敛速度和物体运动的速度关系，只有当算法的收敛速度快于物体运动速度，该算法才可以实时跟踪到姿态，如果物体运动太快，那么该算法会失效。（说到这里，真心有必要采用动态的步长算法啊！）所以在这里，我们让α尽可能大，用于跟踪物体高速运动（不能太大，太大了会导致静态性能差）。那么此时  就比较大，由于β比较小，所以上式就近似为：

由于α假设为比较大的值，那么对于梯度下降法而言：

该公式右边的  就占有绝大比分比例，以至于上次姿态四元数可以忽略不计，也就是说直接由反梯度方向的迭代值就直接可以达到目标姿态，于是有：

现在，可以得到最终的梯度下降法的姿态融合算法公式：

ok，到这里，陀螺仪和加速度计的梯度下降法姿态融合算法就解说完毕，接下来进一步解释融合地磁计的梯度下降算法。其实地磁计的融合算法与先前讨论的加速度计融合算法如出一辙。现在是两者的融合，所以原先有加速计得到的误差函数3X1的  变成了现在的6X1的 

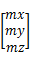
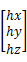
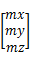
至于[fmx、fmy、fmz]对q求导那部分怎么得来的需要跟大家解释下，我们说磁力计带来了地理坐标系下的基准H={bx, 0, bz}.但是这个可不是常量(地球上任一点的磁场怎么可能是一样的)，那怎么的到呢？还是要由我们的磁力计得到哎。那怎么能行呢，磁力计测的可是B系中的磁场强度，那就先转到换到N系中呗。这里我们第一次用到了B2N矩阵，其实就是N2B阵的转置。经过B2N旋转之后得到N系中的，根据地磁场矢量分解定理，bx^2=hx^2 + hy^2; bz=hz.现在就得到了{bx, 0, bz},再把它经N2B转到B系中，跟B系中的作差就得到上面那个误差函数了。有了误差函数，继续求偏导取得jacobian矩阵，下面过程和上面同理。、

附上9轴梯度下降法的图解