MATLAB利用菲涅尔公式仿真光的折射

从空气进入石英玻璃，计算振幅反射率、透射率和对应的绝对值：

clear;
close all;

n1 = 1;   %空气折射率
n2 = 1.45;%平板玻璃折射率
theta = 0:0.1:90;%角度从0到90
a = theta*pi/180;%角度转化为弧度
rp = (n2*cos(a)-n1*sqrt(1-(n1/n2)^2*(sin(a)).^2))./(n2*cos(a)+n1*sqrt(1-(n1/n2)^2*(sin(a)).^2));
tp = (2*n1*cos(a))./(n2*cos(a)+n1*sqrt(1-(n1/n2)^2*(sin(a)).^2));
rs = (n1*cos(a)-n2*sqrt(1-(n1/n2)^2*(sin(a)).^2))./(n1*cos(a)+n2*sqrt(1-(n1/n2)^2*(sin(a)).^2));
ts = (2*n1*cos(a))./(n1*cos(a)+n2*sqrt(1-(n1/n2)^2*(sin(a)).^2));

figure(1);
subplot(1,2,1);
plot(theta,rp,'-',theta,rs,'--',theta,abs(rp),':' ,theta,abs(rs),'-.','linewidth',2);
legend('r_p','r_s','|r_p|','|r_s|');
xlabel('\theta_i');
ylabel('Amplitude');
title(['n_1=',num2str(n1),',n_2=',num2str(n2)]);
axis([0 90 -1 1]);
grid on;

subplot(1,2,2);
plot(theta,tp,'-',theta,ts,'--',theta,abs(tp),':' ,theta,abs(ts),'-.','linewidth',2);
legend('t_p','t_s','|t_p|','|t_s|');
xlabel('\theta_i');
ylabel('Amplitude');
title(['n_1=',num2str(n1),',n_2=',num2str(n2)]);
axis([0 90 0 1]);
grid on;

结果如下：

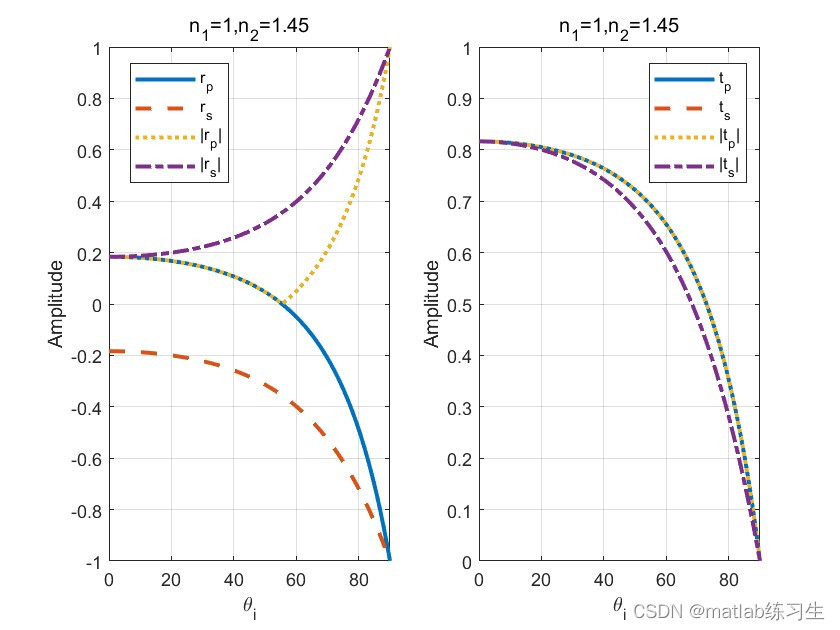
 可以看出：
1、首先，当入射角等于0时，有反射波也有透射波，这个时候并不是完全进入折射率高的介质内；
2、当入射角等于90时，透射波为0，能量完全反射。
3、当角度增大时，投射的两个偏振都减小，反射的s偏振逐渐增大，p偏振先减小再增大。
4、t始终大于0，折射光的相位和入射光始终是一致的；
5、rs始终小于0，表明s偏振光在反射面上发生了π相位变化；
6、rp前期相位变化为0，后期相位相差π。

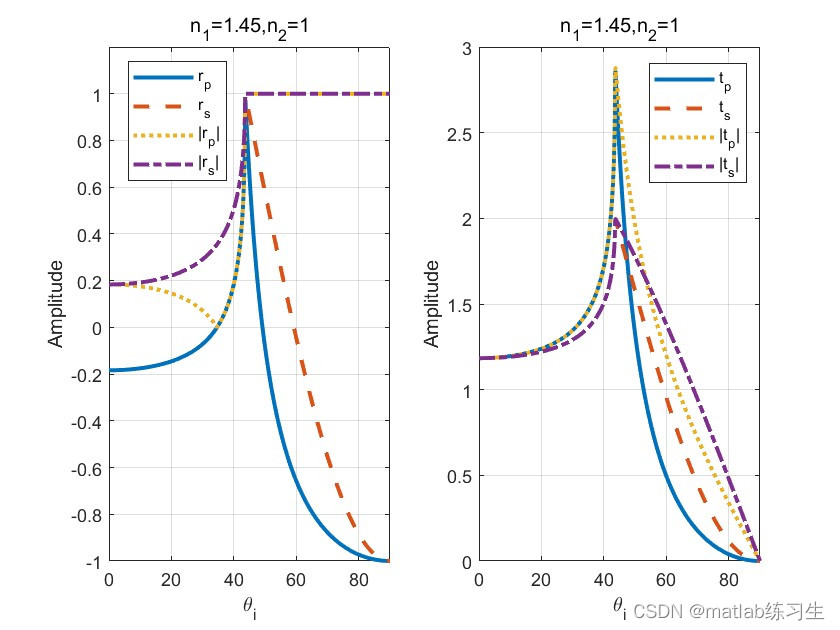
反之，从光密介质进入光疏介质，全反射存在

%从光密到光疏

clear;
close all;

n1 = 1.45;   %空气折射率
n2 = 1;%平板玻璃折射率
theta = 0:0.1:90;%角度从0到90
a = theta*pi/180;%角度转化为弧度
rp = (n2*cos(a)-n1*sqrt(1-(n1/n2)^2*(sin(a)).^2))./(n2*cos(a)+n1*sqrt(1-(n1/n2)^2*(sin(a)).^2));
tp = (2*n1*cos(a))./(n2*cos(a)+n1*sqrt(1-(n1/n2)^2*(sin(a)).^2));
rs = (n1*cos(a)-n2*sqrt(1-(n1/n2)^2*(sin(a)).^2))./(n1*cos(a)+n2*sqrt(1-(n1/n2)^2*(sin(a)).^2));
ts = (2*n1*cos(a))./(n1*cos(a)+n2*sqrt(1-(n1/n2)^2*(sin(a)).^2));

figure(1);
subplot(1,2,1);
plot(theta,rp,'-',theta,rs,'--',theta,abs(rp),':' ,theta,abs(rs),'-.','linewidth',2);
legend('r_p','r_s','|r_p|','|r_s|');
xlabel('\theta_i');
ylabel('Amplitude');
title(['n_1=',num2str(n1),',n_2=',num2str(n2)]);
axis([0 90 -1 1.2]);
grid on;

subplot(1,2,2);
plot(theta,tp,'-',theta,ts,'--',theta,abs(tp),':' ,theta,abs(ts),'-.','linewidth',2);
legend('t_p','t_s','|t_p|','|t_s|');
xlabel('\theta_i');
ylabel('Amplitude');
title(['n_1=',num2str(n1),',n_2=',num2str(n2)]);
axis([0 90 0 3]);
grid on;
可以看出：
1、对于rp仍然存在布鲁斯特角；
2、光密介质进入光疏介质存在全反射现象，rp和rs的绝对值为0；
3、之所以出现如此大的差异，是因为当角度超过全反射角时，rs、rp等为复数。matlab中plot函数在绘图时会忽视复数的虚部。

【例1.4】
对于光密到光疏介质，我们可以计算能流密度来表征：
%从光密到光疏

clear;
close all;

n1 = 1.45;   %空气折射率
n2 = 1;%平板玻璃折射率
theta = 0:0.1:90;%角度从0到90
a = theta*pi/180;%角度转化为弧度
rp = (n2*cos(a)-n1*sqrt(1-(n1/n2)^2*(sin(a)).^2))./(n2*cos(a)+n1*sqrt(1-(n1/n2)^2*(sin(a)).^2));
tp = (2*n1*cos(a))./(n2*cos(a)+n1*sqrt(1-(n1/n2)^2*(sin(a)).^2));
rs = (n1*cos(a)-n2*sqrt(1-(n1/n2)^2*(sin(a)).^2))./(n1*cos(a)+n2*sqrt(1-(n1/n2)^2*(sin(a)).^2));
ts = (2*n1*cos(a))./(n1*cos(a)+n2*sqrt(1-(n1/n2)^2*(sin(a)).^2));

Rp = abs(rp).^2;
Rs = abs(rs).^2;
Rn = (Rp+Rs)/2;

Tp = n2*sqrt(1-(n1/n2)^2*(sin(a)).^2)./(n1*cos(a)).*abs(tp).^2;
Ts = n2*sqrt(1-(n1/n2)^2*(sin(a)).^2)./(n1*cos(a)).*abs(ts).^2;
Tn = (Tp+Ts)/2;

subplot(1,2,1);
plot(theta,Rp,'-',theta,Rs,'-.',theta,Rn,'--','linewidth',2);
legend('R_p','R_s','R_n');
xlabel('\theta_i');
ylabel('Amplitude');
title(['n_1=',num2str(n1),',n_2=',num2str(n2)]);
axis([0 90 0 1]);
grid on;

subplot(1,2,2);
plot(theta,Tp,'-',theta,Ts,'-.',theta,Tn,'--','linewidth',2);
legend('T_p','T_s','T_n');
xlabel('\theta_i');
ylabel('Amplitude');
title(['n_1=',num2str(n1),',n_2=',num2str(n2)]);
axis([0 90 0 1]);
grid on;

结果如下：

 可以看出：
1、对于rp仍然存在布鲁斯特角；
2、光密介质进入光疏介质存在全反射现象，rp和rs的绝对值为0；
3、之所以出现如此大的差异，是因为当角度超过全反射角时，rs、rp等为复数。matlab中plot函数在绘图时会忽视复数的虚部。

来源《高等光学仿真——光波导、激光》