矩阵形式[编辑]
给定直角坐标系的单位向量i,j,k满足下列等式:
- i × j = k j × k = i k × i = j
通过这些规则,两个向量的叉积的坐标可以方便地计算出来,不需要考虑任何角度:设
- a = a 1 i + a 2 j + a 3 k = [ a 1, a 2, a 3]
- b = b 1 i + b 2 j + b 3 k = [ b 1, b 2, b 3]
则
- a × b = [a 2b 3 − a 3b 2, a 3b 1 − a 1b 3, a 1b 2 − a 2b 1]
叉积也可以用四元数来表示。注意到上述i,j,k之间的叉积满足四元数的乘法。一般而言,若将向量[a1, a2, a3]表示成四元数a1i + a2j + a3k,两个向量的叉积可以这样计算:计算两个四元数的乘积得到一个四元数,并将这个四元数的实部去掉,即为结果。更多关于四元数乘法,向量运算及其几何意义请参见四元数与空间旋转。





 本文介绍了如何使用矩阵和四元数方法计算三维空间中两个向量的叉积。通过给出直角坐标系下单位向量i、j、k的叉积规则,详细展示了如何根据这些规则快速计算出任意两个向量的叉积。
本文介绍了如何使用矩阵和四元数方法计算三维空间中两个向量的叉积。通过给出直角坐标系下单位向量i、j、k的叉积规则,详细展示了如何根据这些规则快速计算出任意两个向量的叉积。
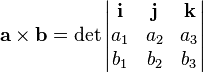
















 1583
1583

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








