清华计算几何大作业（七）:CG2017 PA4-2 Orthogonal Windowing Query （正交矩形窗口查询）

fengkeyleaf

已于 2023-05-23 02:46:16 修改

阅读量452

点赞数 1

分类专栏：计算几何算法文章标签：算法计算几何正交窗口查询 Interval Tree Segment Tree

于 2022-06-12 10:37:49 首次发布

本文链接：https://blog.csdn.net/fengkeyleaf/article/details/125242710

版权

算法同时被 2 个专栏收录

69 篇文章 6 订阅

订阅专栏

计算几何

34 篇文章 20 订阅

订阅专栏

CG2017 PA4-2 Orthogonal Windowing Query （正交矩形窗口查询）

1. 前置知识
2. 思路分析
3. 伪代码
4. 可视化结果示例
5. 项目代码
6. 拓展（Follow-ups）
7. 参考资料
8. 免责声明

1. 前置知识

计算几何算法：Interval Tree, Priority Search Tree, Segment Tree

推荐Interval Tree结合Range Tree（不包含Fractional Cascading），实现起来相对比较简单，Priority Search Tree需要再理解了Interval Tree的基础上，才能比较好地实现。但不使用Fractional Cascading，Interval Tree达不到最优的时间复杂度，但是用来入门解题已经足够了。

另外，Segment Tree对于本题已经属于超纲的方法，可以说是“大炮打蚊子，大材小用”了，因为Segment Tree可以解决任意方向不相交线段的正交矩形窗口查询问题，但幸运地是，题目的输入数据全部都是与坐标轴平行的线段（垂直或水平线段），所以Segment Tree可以当做一个拓展解法，不强制要求。

这里给到必要观看的视频课程章节，这些内容对理解和实现正交矩形窗口查询算法至关重要，标记有绿色√为必看章节（仅包含Interval Tree，有兴趣的童鞋可以自己观看其他空间查找树的章节）：
在这里插入图片描述

2. 思路分析

问题描述：CG2017 PA4-2 Orthogonal Windowing Query （正交矩形窗口查询）

从这个作业开始，难度将是最难的一档，大家需要有一定的心理准备哒~

2.1 Interval Tree

同样，对于Interval Tree教材和视频课程已经讲解的非常详细了，所以这里我们还是把重点放在Degenerate Case上面。对于正交矩形窗口查询，我们同样会遇到退化的情况，而且和平面区域查询相比，这里我们需要处理的情况更加复杂，因为现在输入数据不再是点，而是线段。我们先来看看下面这个非常特殊的案例，即两条处于同一垂直线上的两条垂直线段：
在这里插入图片描述

这里我们还是运用之前的“假象斜切”来处理退化情况的线段，这样好像没有什么问题，相应的Interval Tree我们也顺利的构造出来了，虽然构造方面没有什么问题，但是这样在查询的时候会有一个问题，不知道大家能发现是什么嘛？在给出这个问题之前，我们先来看看上面的Interval Tree进行查询的例子（这种查询就是Stabbing Query，而不是真正意义上的正交矩形窗口查询）：

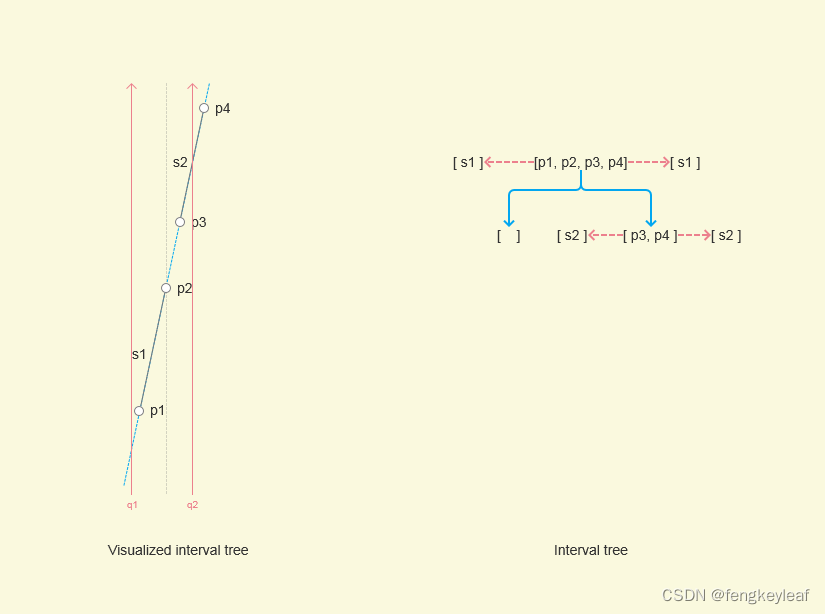
在这里插入图片描述
大家可以看到，现在我们有两个查询点q1 和 q2，按道理它们两个查询都应该把s1和s2报告出来，因为它们两个的x坐标值都是一样，而且s1和s2都处于相同x坐标值的垂直线上面，只是我们进行“假象斜切”，人为地认为两条线段不在同一条垂直线上面。现在问题就已经出现了，大家可以观察到，只有q2可以把两条线段报告出来，但q1不行，因为刚好查询q2的时候路过了两条线段的树节点（及Root和Root的右孩子），可是q1查询的时候只会经过Root，不会经过其右孩子，而是往左孩子方向查询，那自然也不能报告s2了。

更严重地是，我们似乎还没有办法解决这个问题，而且不能去查询没有经过的另一侧子树，因为这样最坏情况会遍历整个树结构，时间复杂度会大幅退化为O(n)，这是不能被接受的。其实无法解决的原因很简单，在这种情况下，其实我们把x坐标忽略了，反而转向查询y坐标，所以问题由原先的x坐标的Stabbing Query，转化为了y坐标的Stabbing Query。但很幸运地是，解决方法也不难实现，其实就是特殊情况特殊处理，根据笔者的观察总结，一共有下面两种解决方案：

当进行x坐标Stabbing Query，则把所有垂直线单独拿出来，对它们构造给予y坐标的Interval Tree，每次查询进行两次，一次正常x坐标Stabbing Query，第二次y坐标Stabbing Query。当进行y坐标Stabbing Query，反之亦然。
还是单独把垂直或水平线段拿出来，以x坐标或y坐标作为Key，将它们全部插入到一颗BBST之中，但相同坐标的线段都放在一个桶（Bucket）里面，笔者称这种BBST为桶树（Bucket Tree）。查询方法和上面类似，第一次在Interval Tree中正常查询，第二次在Bucket Tree中查询退化的线段。

通过这样的处理，我们就能报告出所有可能的线段了。讲解完这个特殊案例，还有一个稍微简单的退化案例，想必大家应该知道怎么处理了，即有多条线段的某一个端点落在同一条垂直或水平线上：

在这里插入图片描述

这种情况虽然没有之前的案例复杂，但是同样会遇到和之前相同的问题，那么该如何解决呢？其实思路之前我们已经提到过了，当x坐标相同时候，我们转而查询y坐标，那么如果进行x坐标的Stabbing Query，且遇到x坐标相同的情况，那查询的y坐标范围是什么呢？答案非常简单哒，其实就是查询y轴整个范围，即负无穷到正无穷，我们也可以用一个正交矩形区域来表示：

[ qx, qx ] x [ -inf, +inf ]

那么在实现查询算法的时候，我们只要先对(qx, +inf)查询一下，再对(qx, -inf)，查询一次，就能经过所有和qx相同x坐标值的节点，进而报告出所有可能的线段：
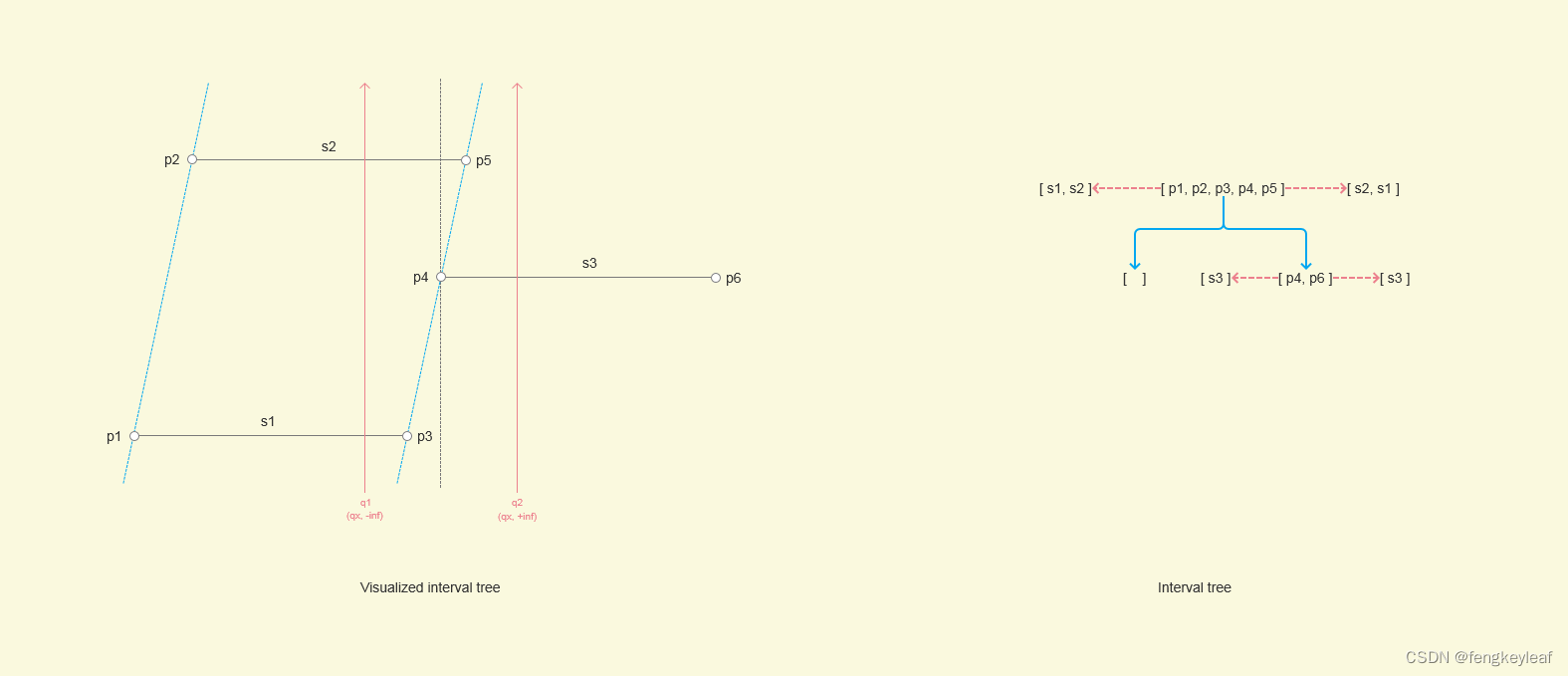
在这里插入图片描述
但是这样处理会需要记录一下哪些线段已经报告过了，避免第二次查询重复报告，具体的实现方法大家可以参考笔者的代码，这里就不详细介绍了。

2.2 Priority Search Tree

Priority Search Tree教材和视频课程已经做了详尽介绍，且也提供了细致的图例，这里也不再赘述，而且它只是把上面Interval Tree中的Associated Structure从Range Tree更改成Priority Search Tree，其余处理思路均和之前保持一致。另外，Priority Queue在单独实现的时候，是可以用Array来实现的，但这里用到的Priority Queue推荐使用真正的二叉树来实现，因为和普通的Priority Queue在结构上还是有所差别的，而且查询逻辑也有些许不同，用二叉树来实现更简单。

2.3 Segment Tree

同样Segment Tree也会遇到和上面相同的退化情况问题，处理的思路也是类似的，查询两次，但需要避免重复报告。对于Segment Tree，笔者着重介绍一下Associated Structure中，线段的排序，教材上面说按照某个节点内线段的垂直方向的顺序进行排序，那么如何在实现的时候，具体如何做呢？

大家需要回忆起Segment Tree中如何划分一段段的区域的，而且线段存储在哪些线段区域，根据笔者的观察，输入线段一定存储在不包含无穷区域的节点里面，这个观察虽然简单，但是很重要，因为我们可以根据线段区间的两个边界值来给线段求交，然后进行垂直方向排序（y轴方向排序），比如教材上面的这个这个例子¹：
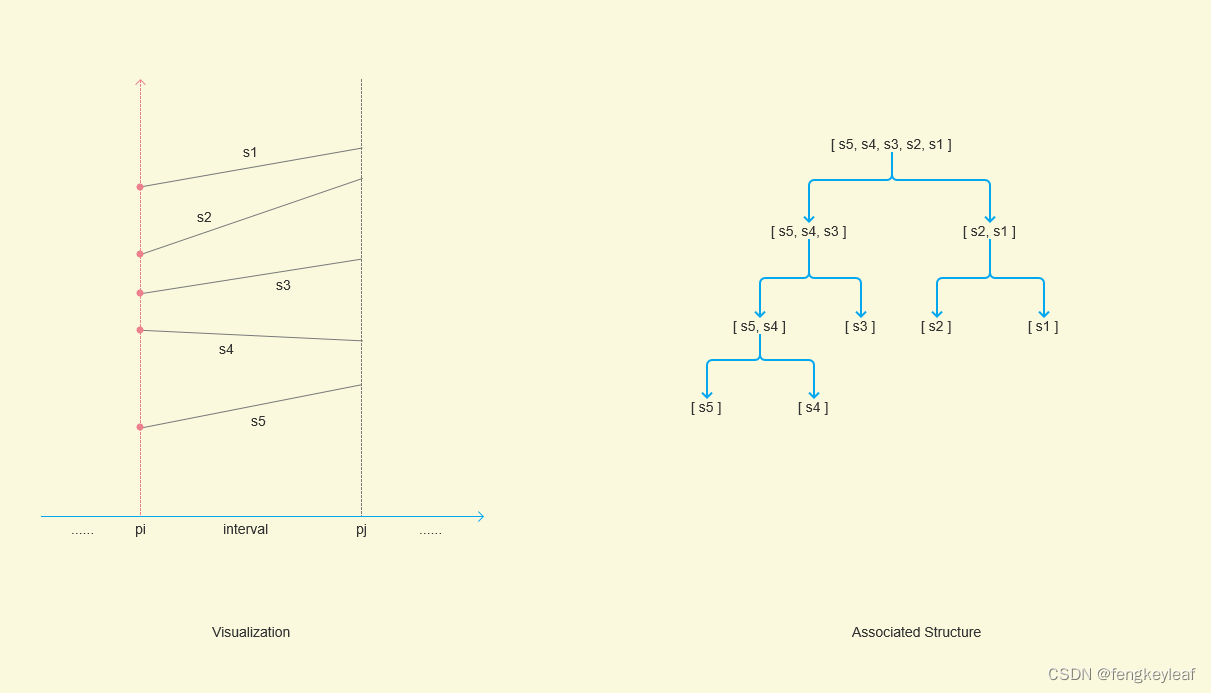
在这里插入图片描述
我们只需要根据线段和垂直线pi的交点排序，就能把线段按照垂直方向进行排序，进而构造出对应的Associated Structure。那么查询的方法也是类似的，以查询左边垂直边界为例：

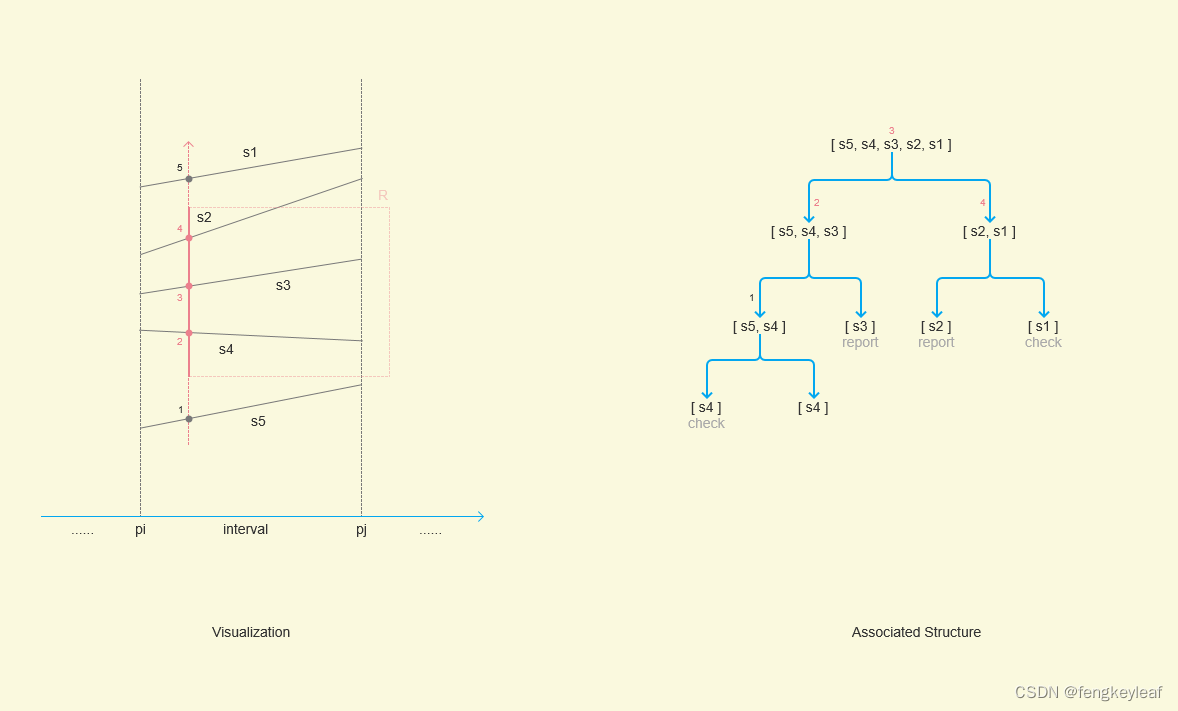
如上图所示，我们只需要根据左边界和线段的交点顺序，就能完成1D Range Query。最后，我们给到三种空间查找树的复杂度对比表格：

数据结构	构造时间复杂度	查询时间复杂度	空间复杂度
Interval Tree	O(nlogn)	O(logn * logn+k)	O(nlogn)
Priority Search Tree	O(nlogn)	O(logn * logn+k)	O(n)
Segment Tree	O(nlogn)	O(logn * logn+k)	O(nlogn)

※ 上面数据结构的复杂度都是在 2D正交矩形窗口查询情形下成立，Interval Tree 和 Segment Tree 可以单独进行Stabbing Query，查询时间复杂仅为O(logn)。

※ n指空间线段集的个数，k指查询需要报告的线段数。

3. 伪代码

这里只给到Interval Tree相关的伪代码，Priority Search Tree 和 Segment Tree 的伪代码请参考教材。

// 构造Interval Tree
Algorithm CONSTRUCTINTERVALTREE(I)
算法 CONSTRUCTINTERVALTREE(I)
Input. A set I of intervals on the real line.
输入：实轴上的一组区间 I
Output. The root of an interval tree for I.
输出：集合 I 所对应区间树的根节点
1. if I = null
1. if (I = ∅)
	2. then return an empty leaf
	2. then return(一匹空叶子)
	3. else Create a node ν. Compute xmid, the median of the set of interval endpoints, and store xmid with ν.
	3. else 生成一个节点 v 计算全部区间端点的中值 xmid，并将 xmid 存入 v 中
		4. Compute Imid and construct two sorted lists for Imid: a list Lleft(ν) sorted on left endpoint and a list Lright(ν) sorted on right endpoint. Store these two lists at ν.
		4. 计算出 Imid，根据 Imid 构造出两个有序表：所有左端点的有序表 Lleft(v), 所有右端点的有序表 Lright(v), 并将这两个列表存入 v 中
		5. lc(ν) ← CONSTRUCTINTERVALTREE(Ileft)
		5. lc(ν) ← CONSTRUCTINTERVALTREE(Ileft)
		6. rc(ν) ← CONSTRUCTINTERVALTREE(Iright)
		6. rc(ν) ← CONSTRUCTINTERVALTREE(Iright)
		7. return ν
		7. return ν

// 查询Interval Tree
// 注意这里的伪代码只是单独查询Interval Tree，执行Stabbing Query的代码逻辑
// 要使Interval Tree拥有 正交矩形窗口查询 的能力，需要结合Range Tree 或 Fractional Cascading
// 下面的伪代码需要进行部分调整
Algorithm QUERYINTERVALTREE(ν,qx)
算法 QUERYINTERVALTREE(v, qx)
Input. The root ν of an interval tree and a query point qx.
输入：以 v 为根节点的一棵区间树，以及一个待查询点 qx
Output. All intervals that contain qx.
输出：包含 qx的所有区间
1. if ν is not a leaf
1. if (v 不是叶子)
	2. then if qx < xmid(ν)
	2. then if (qx < xmid(v))
		3. then Walk along the list Lleft(ν), starting at the interval with the leftmost endpoint, reporting all the intervals that contain qx. Stop as soon as an interval does not contain qx.
		3. then 遍历列表 Lleft(v)：从其中最左侧端点所属的区间开始，逐一报告出包含 qx的各区间,一旦到达不包含 qx的（第）一个区间，即终止遍历
		4. QUERYINTERVALTREE(lc(ν),qx)
		4. QUERYINTERVALTREE(lc(ν),qx)
	5. else Walk along the list Lright(ν), starting at the interval with the rightmost endpoint, reporting all the intervals that contain qx. Stop as soon as an interval does not contain qx.
	5. else 遍历列表 Lright(v)：从其中最右侧端点所属的区间开始，逐一报告出包含 qx的各区间,一旦到达不包含 qx的（第）一个区间，即终止遍历
		6. QUERYINTERVALTREE(rc(ν),qx)
		6. QUERYINTERVALTREE(rc(ν),qx)

4. 可视化结果示例

先给到 Interval Tree 和 Segment Tree 单独使用所涉及的Stabbing Query：
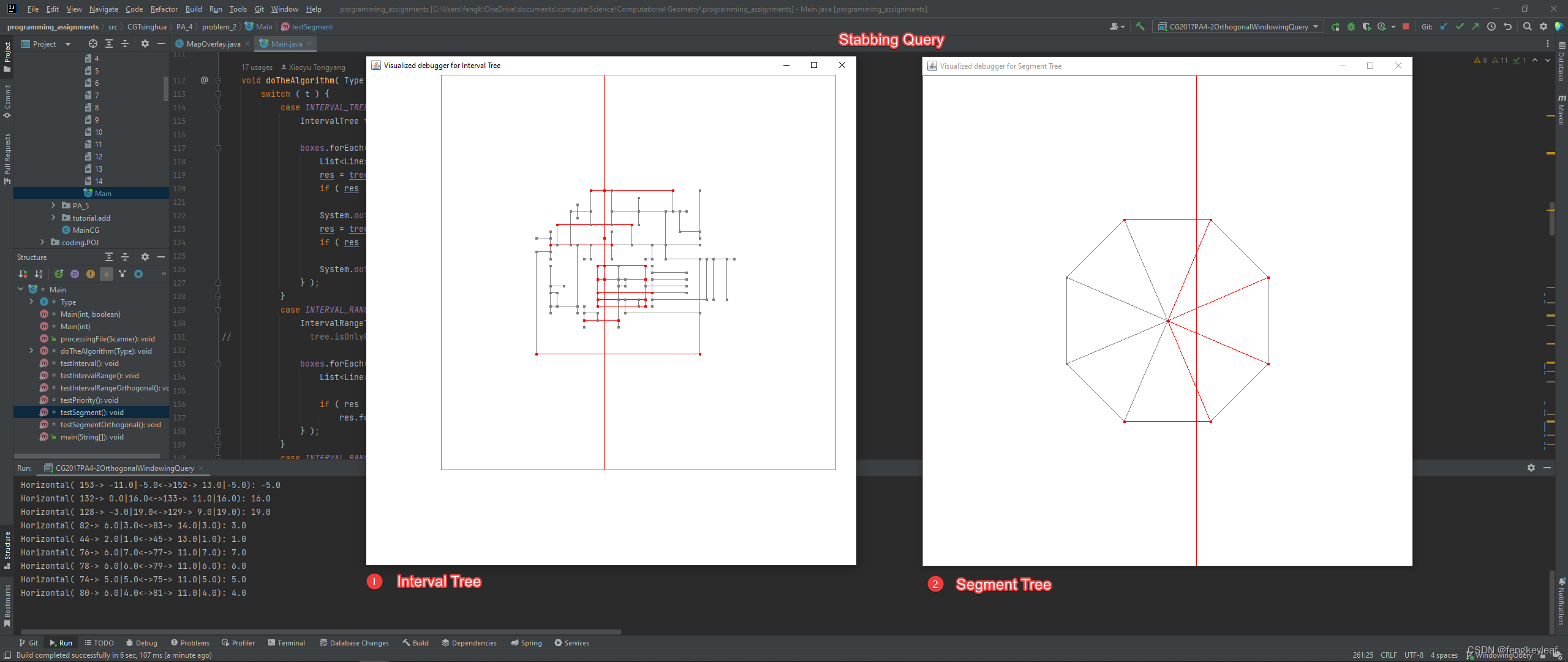
在这里插入图片描述
其次，这里也给到三种空间范围查找树的可视化结果示例，因为Interval Tree和Priority Search Tree在可视化上面没有区别，所以两者共用一个可视化结果：

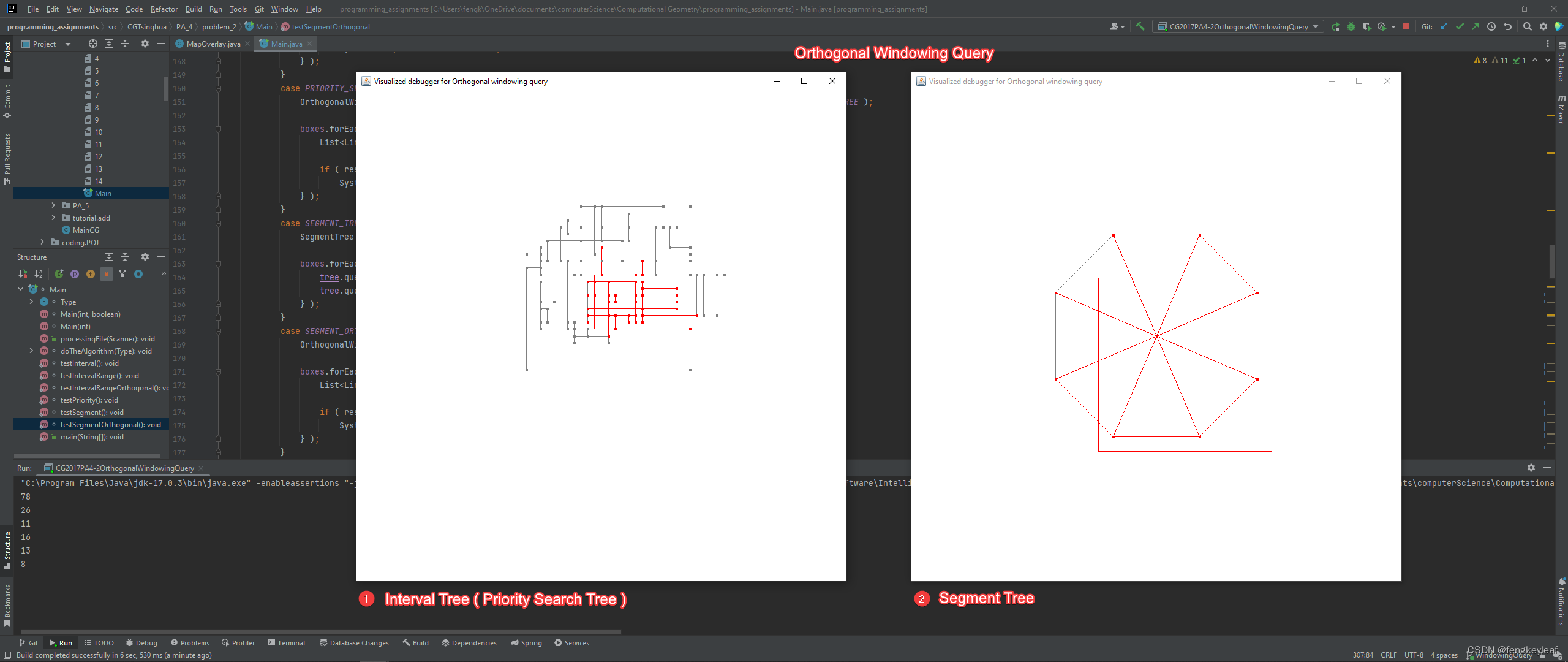
5. 项目代码

个人作业项目代码：Algorithm

Description	Entry method\File
Build Interval Tree	IntervalNode build( List<LineNode> I )
Stabbing query with Interval Tree	List<Line> query( Vector q )
Build Interval Tree combing Range Tree	IntervalRangeNode build( List<LineNode> I )
Windowing query in Interval Range Tree	List<Line> query( List<Vector> R )
Build Interval Tree combing Priority Search Tree	PriorityNode build( List<LineNode> I )
Windowing query in Priority Interval Tree	List<Vector> query( QueryVector[] R )
Build Segment Tree	SegmentNode build( List<Interval> I )
Stabbing query with Segment Tree	List<Line> query( Vector q )
Build Segment Tree combing Range Tree	SegmentRangeNode build( List<Interval> I )
Windowing query in Segment Range Tree	List<Line> query( List<Vector> R )
Program ( including visualization )	CG2017 PA4-2 Orthogonal Windowing Query

6. 拓展（Follow-ups）

实现 Interval Tree 和 Segment Tree 的 Stabbing Query （这个是这两种树单独使用的功能）； - 笔者代码已实现
Interval Tree结合Fractional Cascading，以达到最佳时间复杂度； - 笔者代码已实现
实现其他空间查询树：Priority Search Tree, Segment Tree； - 笔者代码已实现
允许输入线段任意方向，且可相交，思路详见教材 16. 单纯形区域查找：再论截窗（16 Simplex Range Searching: Windowing Revisited）；

上一节：CG2017 PA4-1 Planar Range Query （平面区域查询）

下一节：CG2017 PA2-2 Find Dancing Partners (寻找舞伴)

系列汇总：清华计算几何大作业思路分析和代码实现

7. 参考资料

Computational Geometry: Algorithms and Applications
计算几何 ⎯⎯ 算法与应用, 邓俊辉译，清华大学出版社
计算几何 | Computational Geometry

8. 免责声明

※ 本文之中如有错误和不准确的地方，欢迎大家指正哒~
※ 此项目仅用于学习交流，请不要用于任何形式的商用用途，谢谢呢；

在这里插入图片描述

Computational Geometry: Algorithms and Applications ↩︎

fengkeyleaf

关注

1
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
清华计算几何大作业（七）:CG2017 PA4-2 Orthogonal Windowing Query （正交矩形窗口查询）

清华计算几何大作业（七）:CG2017 PA4-2 Orthogonal Windowing Query （正交矩形窗口查询）
复制链接

扫一扫