在统计计算中,最大期望(EM)算法是在概率(probabilistic)模型中寻找参数最大似然估计的算法,其中概率模型依赖于无法观测的隐藏 变量(Latent Variable)。最大期望经常用在机器学习和计算机视觉的数据聚类(Data Clustering) 领域。最大期望算法经过两个步骤交替进行计算,第一步是计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;第二步是最大化(M),最大 化在 E 步上求得的最大似然值来计算参数的值。M 步上找到的参数估计值被用于下一个 E 步计算中,这个过程不断交替进行。
最大期望值算法由 Arthur Dempster,Nan Laird和Donald Rubin在他们1977年发表的经典论文中提出。他们指出此方法之前其实已经被很多作者”在他们特定的研究领域中多次提出过”。
我们用 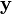 表示能够观察到的不完整的变量值,用
表示能够观察到的不完整的变量值,用  表示无法观察到的变量值,这样
表示无法观察到的变量值,这样  和
和 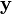 一起组成了完整的数据。
一起组成了完整的数据。 可能是实际测量丢失的数据,也可能是能够简化问题的隐藏变量,如果它的值能够知道的话。例如,在混合模型(Mixture Model)中,如果“产生”样本的混合元素成分已知的话最大似然公式将变得更加便利(参见下面的例子)。
可能是实际测量丢失的数据,也可能是能够简化问题的隐藏变量,如果它的值能够知道的话。例如,在混合模型(Mixture Model)中,如果“产生”样本的混合元素成分已知的话最大似然公式将变得更加便利(参见下面的例子)。
估计无法观测的数据
让  代表矢量 θ:
代表矢量 θ: 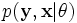 定义的参数的全部数据的概率分布(连续情况下)或者概率聚类函数(离散情况下),那么从这个函数就可以得到全部数据的最大似然值,另外,在给定的观察到的数据条件下未知数据的条件分布可以表示为:
定义的参数的全部数据的概率分布(连续情况下)或者概率聚类函数(离散情况下),那么从这个函数就可以得到全部数据的最大似然值,另外,在给定的观察到的数据条件下未知数据的条件分布可以表示为:
EM算法有这么两个步骤E和M:
-
Expectation step: Choose
q to maximize
F:
-
-
Maximization step: Choose
θ to maximize
F:
-
举个例子吧:高斯混合
假设 x = (x1,x2,…,xn) 是一个独立的观测样本,来自两个多元d维正态分布的混合, 让z=(z1,z2,…,zn)是潜在变量,确定其中的组成部分,是观测的来源.
即:
-
 and
and

where
-
 and
and

目标呢就是估计下面这些参数了,包括混合的参数以及高斯的均值很方差:
似然函数:
where  是一个指示函数 ,f 是 一个多元正态分布的概率密度函数. 可以写成指数形式:
是一个指示函数 ,f 是 一个多元正态分布的概率密度函数. 可以写成指数形式:
下面就进入两个大步骤了:
E-step
给定目前的参数估计 θ(t), Zi 的条件概率分布是由贝叶斯理论得出,高斯之间用参数 τ加权:
-
 .
.
因此,E步骤的结果:
M步骤
Q(θ|θ(t))的二次型表示可以使得 最大化θ相对简单. τ, (μ1,Σ1) and (μ2,Σ2) 可以单独的进行最大化.
首先考虑 τ, 有条件τ1 + τ2=1:
和MLE的形式是类似的,二项分布 , 因此:
下一步估计 (μ1,Σ1):
和加权的 MLE就正态分布来说类似
-
 and
and

对称的:
-
 and
and
 .
.
-
这个例子来自Answers.com的Expectation-maximization algorithm,由于还没有深入体验,心里还说不出一些更通俗易懂的东西来,等研究了并且应用了可能就有所理解和消化。另外,liuxqsmile也做了一些理解和翻译。
============
在网上的源码不多,有一个很好的EM_GM.m,是滑铁卢大学的Patrick P. C. Tsui写的,拿来分享一下:
运行的时候可以如下进行初始化:
X = zeros(600,2); X(1:200,:) = normrnd(0,1,200,2); X(201:400,:) = normrnd(0,2,200,2); X(401:600,:) = normrnd(0,3,200,2); [W,M,V,L] = EM_GM(X,3,[],[],1,[])
下面是程序源码:
function [W,M,V,L] = EM_GM(X,k,ltol,maxiter,pflag,Init)
% [W,M,V,L] = EM_GM(X,k,ltol,maxiter,pflag,Init)
%
% EM algorithm for k multidimensional Gaussian mixture estimation
%
% Inputs:
% X(n,d) - input data, n=number of observations, d=dimension of variable
% k - maximum number of Gaussian components allowed
% ltol - percentage of the log likelihood difference between 2 iterations ([] for none)
% maxiter - maximum number of iteration allowed ([] for none)
% pflag - 1 for plotting GM for 1D or 2D cases only, 0 otherwise ([] for none)
% Init - structure of initial W, M, V: Init.W, Init.M, Init.V ([] for none)
%
% Ouputs:
% W(1,k) - estimated weights of GM
% M(d,k) - estimated mean vectors of GM
% V(d,d,k) - estimated covariance matrices of GM
% L - log likelihood of estimates
%
% Written by
% Patrick P. C. Tsui,
% PAMI research group
% Department of Electrical and Computer Engineering
% University of Waterloo,
% March, 2006
%
%%%% Validate inputs %%%%
if nargin <= 1,
disp('EM_GM must have at least 2 inputs: X,k!/n')
return
elseif nargin == 2,
ltol = 0.1; maxiter = 1000; pflag = 0; Init = [];
err_X = Verify_X(X);
err_k = Verify_k(k);
if err_X | err_k, return; end
elseif nargin == 3,
maxiter = 1000; pflag = 0; Init = [];
err_X = Verify_X(X);
err_k = Verify_k(k);
[ltol,err_ltol] = Verify_ltol(ltol);
if err_X | err_k | err_ltol, return; end
elseif nargin == 4,
pflag = 0; Init = [];
err_X = Verify_X(X);
err_k = Verify_k(k);
[ltol,err_ltol] = Verify_ltol(ltol);
[maxiter,err_maxiter] = Verify_maxiter(maxiter);
if err_X | err_k | err_ltol | err_maxiter, return; end
elseif nargin == 5,
Init = [];
err_X = Verify_X(X);
err_k = Verify_k(k);
[ltol,err_ltol] = Verify_ltol(ltol);
[maxiter,err_maxiter] = Verify_maxiter(maxiter);
[pflag,err_pflag] = Verify_pflag(pflag);
if err_X | err_k | err_ltol | err_maxiter | err_pflag, return; end
elseif nargin == 6,
err_X = Verify_X(X);
err_k = Verify_k(k);
[ltol,err_ltol] = Verify_ltol(ltol);
[maxiter,err_maxiter] = Verify_maxiter(maxiter);
[pflag,err_pflag] = Verify_pflag(pflag);
[Init,err_Init]=Verify_Init(Init);
if err_X | err_k | err_ltol | err_maxiter | err_pflag | err_Init, return; end
else
disp('EM_GM must have 2 to 6 inputs!');
return
end
%%%% Initialize W, M, V,L %%%%
t = cputime;
if isempty(Init),
[W,M,V] = Init_EM(X,k); L = 0;
else
W = Init.W;
M = Init.M;
V = Init.V;
end
Ln = Likelihood(X,k,W,M,V); % Initialize log likelihood
Lo = 2*Ln;
%%%% EM algorithm %%%%
niter = 0;
while (abs(100*(Ln-Lo)/Lo)>ltol) & (niter<=maxiter),
E = Expectation(X,k,W,M,V); % E-step
[W,M,V] = Maximization(X,k,E); % M-step
Lo = Ln;
Ln = Likelihood(X,k,W,M,V);
niter = niter + 1;
end
L = Ln;
%%%% Plot 1D or 2D %%%%
if pflag==1,
[n,d] = size(X);
if d>2,
disp('Can only plot 1 or 2 dimensional applications!/n');
else
Plot_GM(X,k,W,M,V);
end
elapsed_time = sprintf('CPU time used for EM_GM: %5.2fs',cputime-t);
disp(elapsed_time);
disp(sprintf('Number of iterations: %d',niter-1));
end
%%%%%%%%%%%%%%%%%%%%%%
%%%% End of EM_GM %%%%
%%%%%%%%%%%%%%%%%%%%%%
function E = Expectation(X,k,W,M,V)
[n,d] = size(X);
a = (2*pi)^(0.5*d);
S = zeros(1,k);
iV = zeros(d,d,k);
for j=1:k,
if V(:,:,j)==zeros(d,d), V(:,:,j)=ones(d,d)*eps; end
S(j) = sqrt(det(V(:,:,j)));
iV(:,:,j) = inv(V(:,:,j));
end
E = zeros(n,k);
for i=1:n,
for j=1:k,
dXM = X(i,:)'-M(:,j);
pl = exp(-0.5*dXM'*iV(:,:,j)*dXM)/(a*S(j));
E(i,j) = W(j)*pl;
end
E(i,:) = E(i,:)/sum(E(i,:));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Expectation %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [W,M,V] = Maximization(X,k,E)
[n,d] = size(X);
W = zeros(1,k); M = zeros(d,k);
V = zeros(d,d,k);
for i=1:k, % Compute weights
for j=1:n,
W(i) = W(i) + E(j,i);
M(:,i) = M(:,i) + E(j,i)*X(j,:)';
end
M(:,i) = M(:,i)/W(i);
end
for i=1:k,
for j=1:n,
dXM = X(j,:)'-M(:,i);
V(:,:,i) = V(:,:,i) + E(j,i)*dXM*dXM';
end
V(:,:,i) = V(:,:,i)/W(i);
end
W = W/n;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Maximization %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function L = Likelihood(X,k,W,M,V)
% Compute L based on K. V. Mardia, "Multivariate Analysis", Academic Press, 1979, PP. 96-97
% to enchance computational speed
[n,d] = size(X);
U = mean(X)';
S = cov(X);
L = 0;
for i=1:k,
iV = inv(V(:,:,i));
L = L + W(i)*(-0.5*n*log(det(2*pi*V(:,:,i))) ...
-0.5*(n-1)*(trace(iV*S)+(U-M(:,i))'*iV*(U-M(:,i))));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Likelihood %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%
function err_X = Verify_X(X)
err_X = 1;
[n,d] = size(X);
if n<d,
disp('Input data must be n x d!/n');
return
end
err_X = 0;
%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Verify_X %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%
function err_k = Verify_k(k)
err_k = 1;
if ~isnumeric(k) | ~isreal(k) | k<1,
disp('k must be a real integer >= 1!/n');
return
end
err_k = 0;
%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Verify_k %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%
function [ltol,err_ltol] = Verify_ltol(ltol)
err_ltol = 1;
if isempty(ltol),
ltol = 0.1;
elseif ~isreal(ltol) | ltol<=0,
disp('ltol must be a positive real number!');
return
end
err_ltol = 0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Verify_ltol %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [maxiter,err_maxiter] = Verify_maxiter(maxiter)
err_maxiter = 1;
if isempty(maxiter),
maxiter = 1000;
elseif ~isreal(maxiter) | maxiter<=0,
disp('ltol must be a positive real number!');
return
end
err_maxiter = 0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Verify_maxiter %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [pflag,err_pflag] = Verify_pflag(pflag)
err_pflag = 1;
if isempty(pflag),
pflag = 0;
elseif pflag~=0 & pflag~=1,
disp('Plot flag must be either 0 or 1!/n');
return
end
err_pflag = 0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Verify_pflag %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [Init,err_Init] = Verify_Init(Init)
err_Init = 1;
if isempty(Init),
% Do nothing;
elseif isstruct(Init),
[Wd,Wk] = size(Init.W);
[Md,Mk] = size(Init.M);
[Vd1,Vd2,Vk] = size(Init.V);
if Wk~=Mk | Wk~=Vk | Mk~=Vk,
disp('k in Init.W(1,k), Init.M(d,k) and Init.V(d,d,k) must equal!/n')
return
end
if Md~=Vd1 | Md~=Vd2 | Vd1~=Vd2,
disp('d in Init.W(1,k), Init.M(d,k) and Init.V(d,d,k) must equal!/n')
return
end
else
disp('Init must be a structure: W(1,k), M(d,k), V(d,d,k) or []!');
return
end
err_Init = 0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Verify_Init %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [W,M,V] = Init_EM(X,k)
[n,d] = size(X);
[Ci,C] = kmeans(X,k,'Start','cluster', ...
'Maxiter',100, ...
'EmptyAction','drop', ...
'Display','off'); % Ci(nx1) - cluster indeices; C(k,d) - cluster centroid (i.e. mean)
while sum(isnan(C))>0,
[Ci,C] = kmeans(X,k,'Start','cluster', ...
'Maxiter',100, ...
'EmptyAction','drop', ...
'Display','off');
end
M = C';
Vp = repmat(struct('count',0,'X',zeros(n,d)),1,k);
for i=1:n, % Separate cluster points
Vp(Ci(i)).count = Vp(Ci(i)).count + 1;
Vp(Ci(i)).X(Vp(Ci(i)).count,:) = X(i,:);
end
V = zeros(d,d,k);
for i=1:k,
W(i) = Vp(i).count/n;
V(:,:,i) = cov(Vp(i).X(1:Vp(i).count,:));
end
%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Init_EM %%%%
%%%%%%%%%%%%%%%%%%%%%%%%
function Plot_GM(X,k,W,M,V)
[n,d] = size(X);
if d>2,
disp('Can only plot 1 or 2 dimensional applications!/n');
return
end
S = zeros(d,k);
R1 = zeros(d,k);
R2 = zeros(d,k);
for i=1:k, % Determine plot range as 4 x standard deviations
S(:,i) = sqrt(diag(V(:,:,i)));
R1(:,i) = M(:,i)-4*S(:,i);
R2(:,i) = M(:,i)+4*S(:,i);
end
Rmin = min(min(R1));
Rmax = max(max(R2));
R = [Rmin:0.001*(Rmax-Rmin):Rmax];
clf, hold on
if d==1,
Q = zeros(size(R));
for i=1:k,
P = W(i)*normpdf(R,M(:,i),sqrt(V(:,:,i)));
Q = Q + P;
plot(R,P,'r-'); grid on,
end
plot(R,Q,'k-');
xlabel('X');
ylabel('Probability density');
else % d==2
plot(X(:,1),X(:,2),'r.');
for i=1:k,
Plot_Std_Ellipse(M(:,i),V(:,:,i));
end
xlabel('1^{st} dimension');
ylabel('2^{nd} dimension');
axis([Rmin Rmax Rmin Rmax])
end
title('Gaussian Mixture estimated by EM');
%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Plot_GM %%%%
%%%%%%%%%%%%%%%%%%%%%%%%
function Plot_Std_Ellipse(M,V)
[Ev,D] = eig(V);
d = length(M);
if V(:,:)==zeros(d,d),
V(:,:) = ones(d,d)*eps;
end
iV = inv(V);
% Find the larger projection
P = [1,0;0,0]; % X-axis projection operator
P1 = P * 2*sqrt(D(1,1)) * Ev(:,1);
P2 = P * 2*sqrt(D(2,2)) * Ev(:,2);
if abs(P1(1)) >= abs(P2(1)),
Plen = P1(1);
else
Plen = P2(1);
end
count = 1;
step = 0.001*Plen;
Contour1 = zeros(2001,2);
Contour2 = zeros(2001,2);
for x = -Plen:step:Plen,
a = iV(2,2);
b = x * (iV(1,2)+iV(2,1));
c = (x^2) * iV(1,1) - 1;
Root1 = (-b + sqrt(b^2 - 4*a*c))/(2*a);
Root2 = (-b - sqrt(b^2 - 4*a*c))/(2*a);
if isreal(Root1),
Contour1(count,:) = [x,Root1] + M';
Contour2(count,:) = [x,Root2] + M';
count = count + 1;
end
end
Contour1 = Contour1(1:count-1,:);
Contour2 = [Contour1(1,:);Contour2(1:count-1,:);Contour1(count-1,:)];
plot(M(1),M(2),'k+');
plot(Contour1(:,1),Contour1(:,2),'k-');
plot(Contour2(:,1),Contour2(:,2),'k-');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Plot_Std_Ellipse %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%







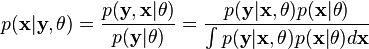




![L(/theta;/mathbf{x},/mathbf{z}) = /exp /left/{ /sum_{i=1}^n /sum_{j=1}^2 /mathbb{I}(z_i=j) /big[ /log /tau_j -/tfrac{1}{2} /log |/Sigma_j| -/tfrac{1}{2}(/mathbf{x}_i-/boldsymbol{/mu}_j)^/top/Sigma_j^{-1} (/mathbf{x}_i-/boldsymbol{/mu}_j) -/tfrac{d}{2} /log(2/pi) /big] /right/}](http://wpcontent.answcdn.com/math/d/5/3/d53e50b61c8d3465b6bd20e085933f6a.png)
![/begin{align}Q(/theta|/theta^{(t)}) &= /operatorname{E} [/log L(/theta;/mathbf{x},/mathbf{Z}) ] // &= /sum_{i=1}^n /sum_{j=1}^2 T_{j,i}^{(t)} /big[ /log /tau_j -/tfrac{1}{2} /log |/Sigma_j| -/tfrac{1}{2}(/mathbf{x}_i-/boldsymbol{/mu}_j)^/top/Sigma_j^{-1} (/mathbf{x}_i-/boldsymbol{/mu}_j) -/tfrac{d}{2} /log(2/pi) /big] /end{align}](http://wpcontent.answcdn.com/math/8/4/e/84efae4d173871c8ffb2f53a0c67595f.png)
![/begin{align}/boldsymbol{/tau}^{(t+1)} &= /underset{/boldsymbol{/tau}} /operatorname{arg/,max}/ Q(/theta | /theta^{(t)} ) // &= /underset{/boldsymbol{/tau}} /operatorname{arg/,max} / /left/{ /left[ /sum_{i=1}^n T_{1,i}^{(t)} /right] /log /tau_1 + /left[ /sum_{i=1}^n T_{2,i}^{(t)} /right] /log /tau_2 /right/} /end{align}](http://wpcontent.answcdn.com/math/d/c/8/dc83eff0611209a985b5671d8059f072.png)
















 999
999











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








