ML旅程——第一站：SVM学习笔记（2）

尝心酒余味丶

已于 2024-02-29 22:29:27 修改

阅读量888

点赞数 22

文章标签：支持向量机学习笔记

于 2024-02-29 19:46:49 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/g768964308/article/details/136376910

版权

1 支持向量机模型（线性可分）

图1

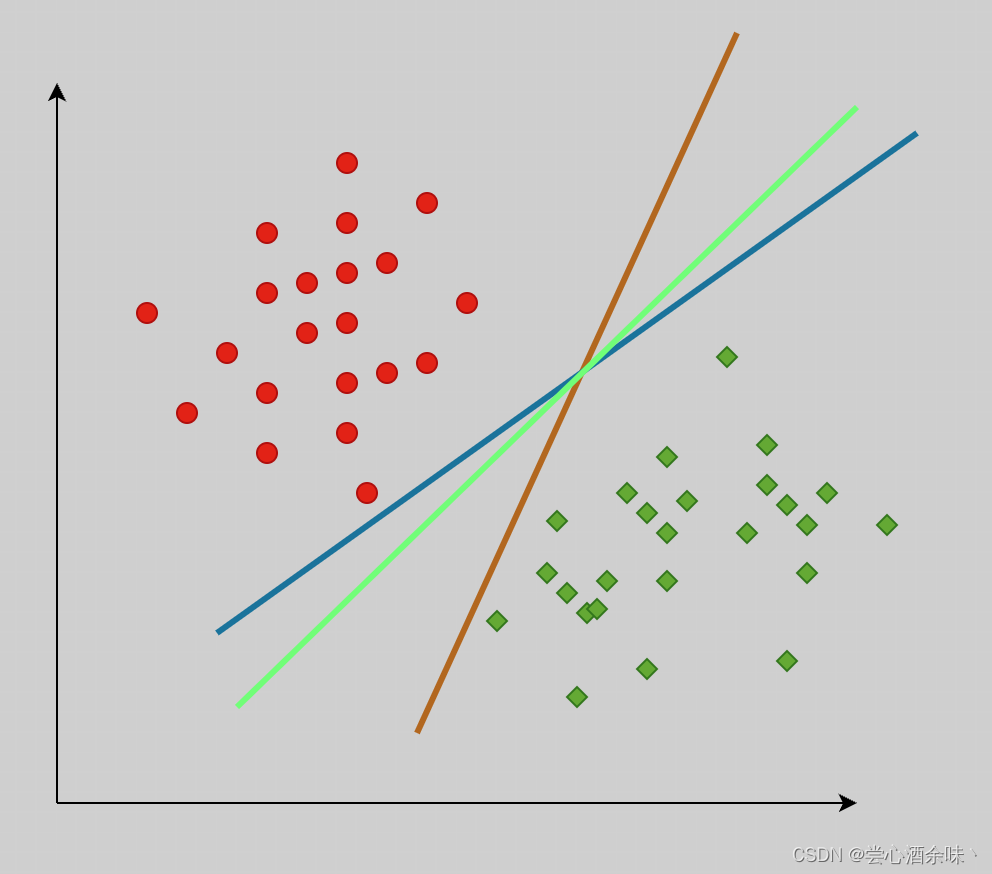
引入一个问题：假如我们有图1所示的两簇点集，我们需要一条线（分类模型）来将两簇点分别开来，我们该如何划线呢？理论上，如果没有什么特殊要求的话，这样的线可以画无数条。

那么那一条线是比较好的呢？很多人直观上都会觉得是中间绿色的那条。

那么有什么办法评价这条线到底好不好呢？

SVM的发明者Vapnik定义了一种衡量这条线的准则来巧妙的解释了上述疑问。

图2

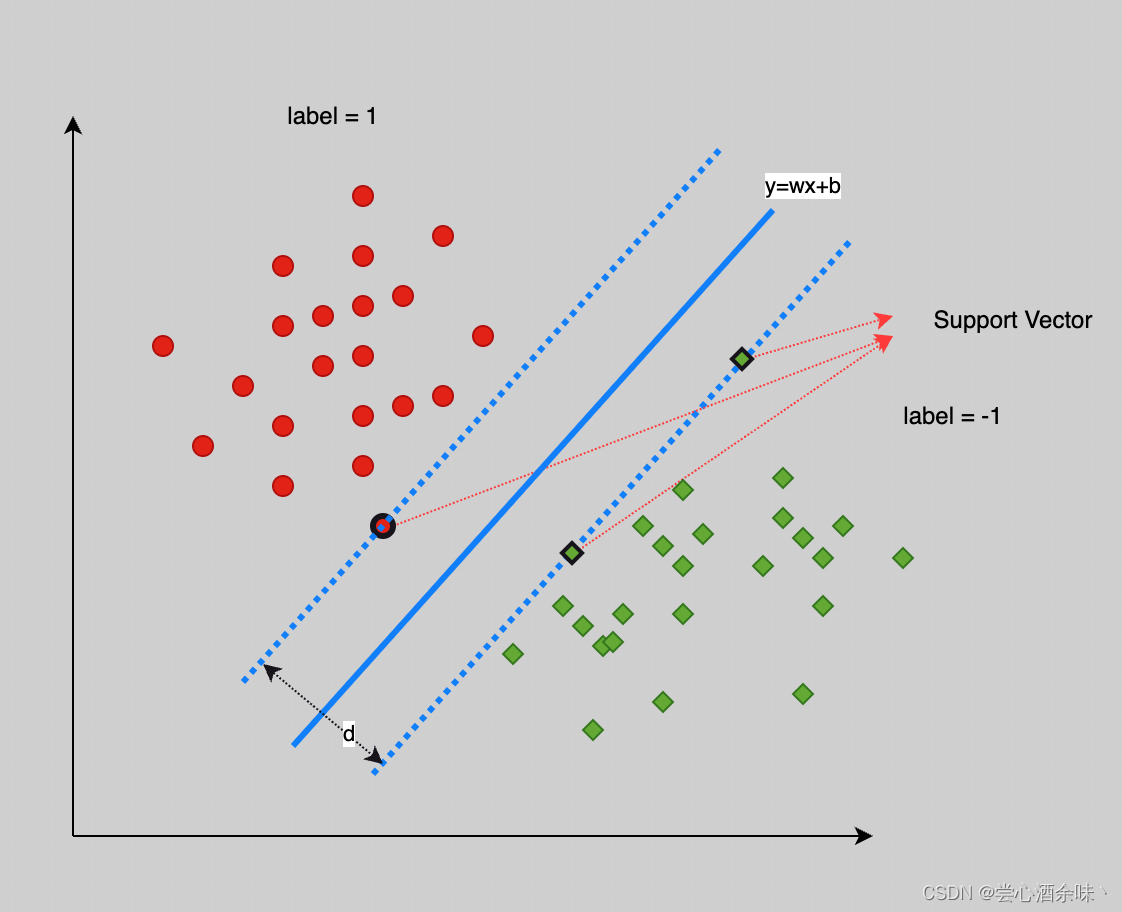
如图2所示，定义一条直线，让它在两簇点之间上下平行移动，当其与某类点相交时为边界，则会在最初定义直线的两侧找到两侧边界，如图2所示。中间将两类点分开的“线”（有一定的平移范围），实际也有无数个。遂产生了两个边界之间间隔d（Margin）的衡量标准，Vapnik的观点就是寻找d最大的那条“线”，就是分开这两类点最好的那一条（距离两侧边界相等，均为d/2）。于是，SVM就诞生了。接下来就是如何寻找的问题。

如何将这个问题优雅的用数学表示？下面介绍一些个人了解到的一些知识。

_____________________________________________________________________________

本次笔记主要是阐述，SVM模型是如何建立，其思想历程是怎样的。主要是两个问题：

① 我们怎么样定义上图中划分线的优劣？

② 如何找到这样的线？

* 关于线性可分和线性不可分的概念，想必大家都有自己的理解，这里不再详细介绍，文中会会体现相关定义。

1.1 一些小的概念

$d$ : 间隔（Margin），SVM定义的模型衡量标准，寻找d最大的超平面。

$Support\,\,\,Vector$ : 支持向量，超平面左右边界相交的样本向量。

① 训练样本及标签

有一批样本 $(x_{1}, y_{1}), (x_{2}, y_{2}), ..., (x_{N}, y_{N})$ ，其中 $x_{i}, \,\,\,i=1\sim N$ 是一个向量；

$y_{i}, \,\,\, i=1\sim N$ 是样本标签（即属于哪一种类别）。

② 线性模型

构建一个线性模型（超平面）： $\omega ^{T} x + b =0$ .

其中 $\omega$ 是跟 $x_{i}$ 同维的向量。

③ 一个训练集线性可分是指(数学描述)，

对于一个样本集合 $\left \{ (x_{i}, y_{i}), i=1\sim N \right \}$ ,

$\exists (\omega, b)$ 使得 $\forall i=1 \sim N$ ,

(a) $y_{i} = +1, \,\,\, \omega ^{T}x_{i} + b \ge 0$ ,

(b) $y_{i} = -1, \,\,\, \omega ^{T}x_{i} + b < 0$ ,

上述 (a) 与 (b) 等价于 $y_{i}[\omega ^{T} x_{i} + b] \ge 0$ .

解释：这里假设分类问题是二分类问题，并且把便签类别分别定义为+1和-1（任何形式

都可以，用正负一方便数学表示），所以(a)和(b)中的不等式与 $y_{i}$ 保证同号，遂有上式。

1.2 一些存在的事实

① 对于一个线性模型（超平面） $\omega ^{T}x_{i} + b$ 而言， $a\omega ^{T}x_{i} + ab, a \epsilon \mathbb{R}^{+}$ 表示同样平面。

② 点到线性模型（超平面）的距离（推广自点到直线的距离公式）， $d = \frac{|\omega ^{T}x+b |}{||\omega||}$ 。

1.3 SVM 建立的优化问题

根据SVM建立的超平面优劣的衡量准则，可以将最优线性模型的寻找，定义为下述优化

（如何定义划分的线？）

① 最小化 $||\omega||^{2}$ , 为了求导后的方便，等价于 $\frac{1}{2} ||\omega||^{2}$ .

* 为什么是最小化 $||\omega||^{2}$ ？因为SVM归根结底是要寻找d最大的超平面，那么根据上述事实②，要使得 $d$ 最大，则需要 $\omega$ 最小。

（怎么样找到这个线？）

② 满足限制条件 $y_{i}[\omega ^{T} x_{i} + b] \ge 1, \,\, i=1\sim N$ .

* 这里会有一点小疑问，为什是大于等于1，前文中明明是大于等于0，是不是写错了？其实不然，根据上述事实①我们可以调整a的值来缩放超平面（左右移动超平面），在支持向量处，会有 $|\omega ^{T} x_{i} + b| = 1$ ，这个时候支持向量与平面的距离恰好为 $\frac{d}{2} = \frac {1}{||\omega||}$ , 那么在支持向量外侧的点，自然而然就满足 $|\omega ^{T} x_{i} + b| > 1$ ，所以对于整个样本集合来说，满足上述约束②。

有了上述两个描述，我们只需要想办法寻找最大的Margin $d$ 就可以将超平面找到了。

SVM的巧妙之处，其实是把寻找超平面的优化问题，设置成了一个二次优化（目标函数是二次项，限制条件是一次项）。

（之后继续整理，如何求解上述问题。）

尝心酒余味丶

关注

22
点赞
踩
25

收藏

觉得还不错? 一键收藏
0
评论
ML旅程——第一站：SVM学习笔记（2）

SVM解决分类问题的思路
复制链接

扫一扫

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。