第二章 74181中的先行进位问题

1、说明

$$图1$$

$$图2$$

注：图1中红色方框并不是输入项X和Y的全加器，即与图2中的全加器不相对应。

2、先行进位

在全加器中，输入项A、B、C_n+i，输出项为S、C_n+i+1

$$C_{n+i+1}=A_i{B}_i+B_i{C}_{n+i}+C_{n+i}A$$

$$C_{n+i+1}=A_i{B}_i+(A_i+B_i)C_{n+i}$$

由全加器的真值表得，当输入取反时，输出也取反

$$\overline{C_{n+i+1}}=\overline{A_i}\overline{B_i}+(\overline{A_i}+\overline{B_i})\overline{C_{n+i}}$$

$$\overline{C_{n+i+1}}=\overline{A_i+B_i}+\overline{A_i{B}_i}\bullet \overline{C_{n+i}}$$

$$C_{n+i+1}=\overline{\overline{A_i+B_i}+\overline{A_i{B}_i}\bullet \overline{C_{n+i}}}$$

记：

$$\overline{A_i{B}_i}为X_i$$

$$\overline{A_i+B_i}为Y_i$$

（注：74181中取S₀S₁S₂S₃＝1001时，X与Y的表达式即为上式。）

则

$$C_{n+i+1}=\overline{Y_i+X_i\overline{C_{n+i}}}$$

那么：

$$C_{n+1}=\overline{Y_0+X_0\overline{C_n}}$$

$$C_{n+2}=\overline{Y_1+X_1\overline{C_{n+1}}}$$

$$C_{n+2}=\overline{Y_1+X_1(Y_0+X_0\overline{C_n})}$$

$$C_{n+2}=\overline{Y_1+Y_0{X}_1+X_0{X}_1\overline{C_n}}$$

同理

$$C_{n+3}=\overline{Y_2+Y_1{X}_2+Y_0{X}_1{X}_2+X_0{X}_1{X}_2\overline{C_n}}$$

$$C_{n+4}=\overline{Y_3+Y_2{X}_3+Y_1{X}_2{X}_3+Y_0{X}_1{X}_2{X}_3+X_0{X}_1{X}_2{X}_3\overline{C_n}}$$

记：

$$P=X_0{X}_1{X}_2{X}_3$$

$$G=Y_3+Y_2{X}_3+Y_1{X}_2{X}_3+Y_0{X}_1{X}_2{X}_3$$

得：

$$C_{n+4}=\overline{G+P\overline{C_n}}$$

即：

$$\overline{C_{n+4}}=G+P\overline{C_n}$$

综上所述，可以看到，C_n+i+1与C_n+i之间在取非后存在先行进位关系。

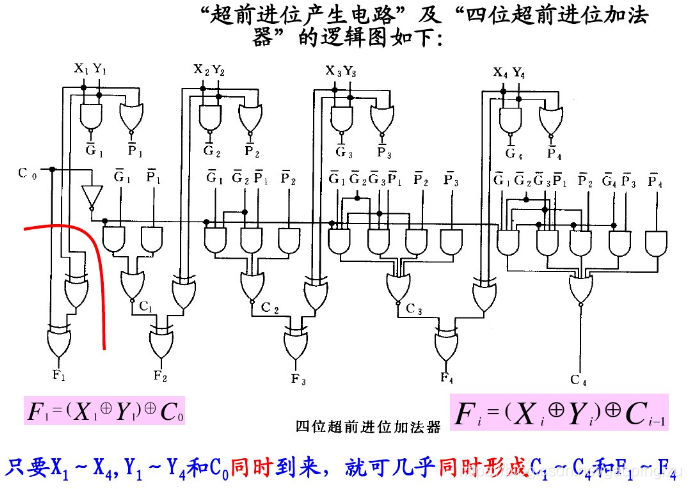
常见的先行进位加法器（超前进位加法器）如下图所示

$$图3－注：图中X、Y对应原A、B；图中P、G对应原X、Y$$

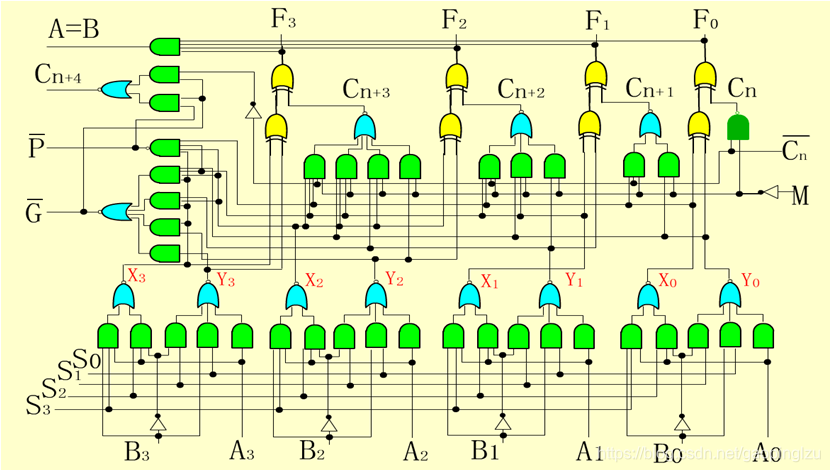
2、图1中的C_n+4

注：图1中P、G与上述内容中所定义不同，需按取反标记，即图1中C_n+4、P、G应标记成：

$$C_{n+4}、\overline{P}、\overline{G}$$

则：

$$C_{n+4}=\overline{\overline{P}\overline{G}+C_n\overline{G}}$$

$$C_{n+4}=\overline{\overline{P}\overline{G}}\bullet \overline{C_n\overline{G}}$$

$$C_{n+4}=(P+G)\bullet (\overline{C_n}+G)$$

$$C_{n+4}=P\overline{C_n}+PG+G\overline{C_n}+G$$

$$C_{n+4}=G+P\overline{C_n}$$

3、图1中的更正