模拟退火算法原理:
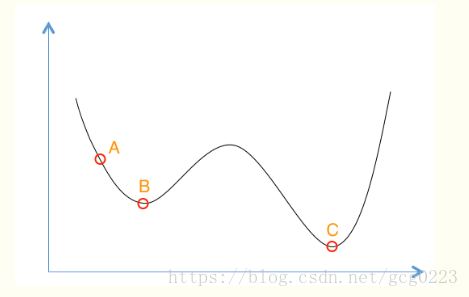
其目标是要找到函数的最大值,若初始化时,初始点的位置在A处,则会寻找到附近的局部最大值B点处,由于B点出是一个局部最大值点,故对于一般算法来讲,比如梯度下降法,该算法无法跳出局部最优值。
模拟退火算法(Simulated Annealing, SA)的思想借鉴于固体的退火原理,当固体的温度很高的时候,内能比较大,固体的内部粒子处于快速无序运动,当温度慢慢降低的过程中,固体的内能减小,粒子的慢慢趋于有序,最终,当固体处于常温时,内能达到最小,此时,粒子最为稳定。模拟退火算法便是基于这样的原理设计而成。
模拟退火算法从某一较高的温度出发,这个温度称为初始温度,伴随着温度参数的不断下降,算法中的解趋于稳定,但是,可能这样的稳定解是一个局部最优解,此时,模拟退火算法中会以一定的概率跳出这样的局部最优解,以寻找目标函数的全局最优解。如上图中所示,若此时寻找到了B点处的解,模拟退火算法会以一定的概率跳出这个解,最终可以如跳到了C点,这样在一定程度上增加了寻找到全局最优解的可能性。
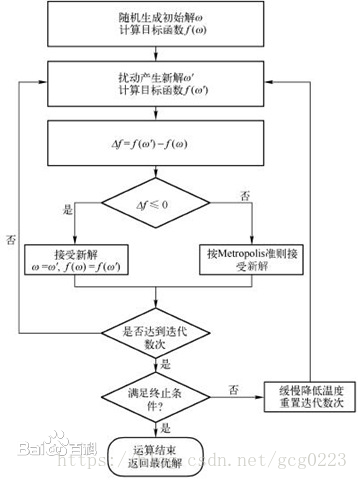
如图为模拟退火的算法流程:
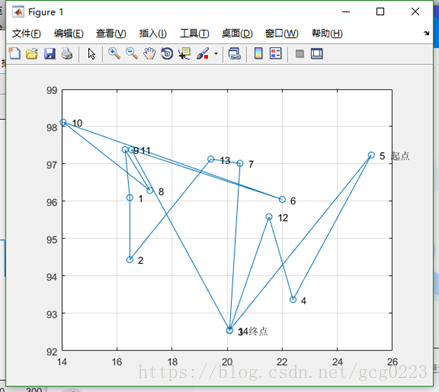
下图是利用模拟退火针对图论中汉密尔顿图求解最短路径问题:
初始解
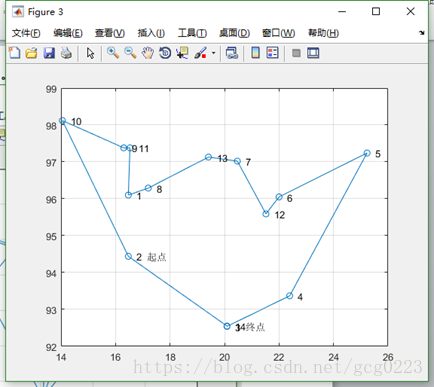
最终解
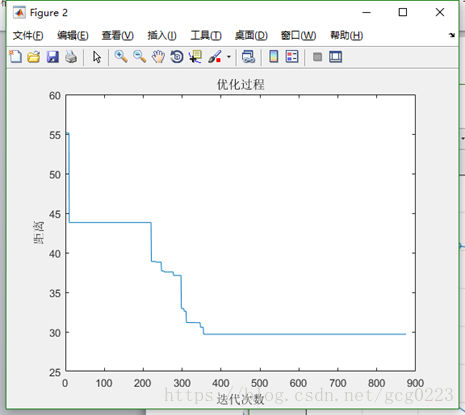
优化过程
总结:
总结:模拟退火最重要的防止进入局部最优解,一般采用Metropolis准则,粒子在温度T时趋于平衡的概率为exp(-ΔE/(kT)),其中E为温度T时的内能,ΔE为其改变数,k为Boltzmann常数。Metropolis准则常表示为:
Metropolis准则表明,在温度为T时,出现能量差为dE的降温的概率为P(dE),表示为:P(dE)= exp( dE/(kT))。其中k是一个常数,exp表示自然指数,且dE<0。所以P和T正相关。这条公式就表示:温度越高,出现一次能量差为dE的降温的概率就越大;温度越低,则出现降温的概率就越小。又由于dE总是小于0(因为退火的过程是温度逐渐下降的过程),因此dE/kT<0 ,所以P(dE)的函数取值范围是(0,1) 。随着温度T的降低,P(dE)会逐渐降低。
总结起来就是:
若f( Y(i+1) ) <= f( Y(i)) (即移动后得到更优解),则总是接受该移动;
若f( Y(i+1) ) > f( Y(i)) (即移动后的解比当前解要差),则以一定的概率接受移动,而且这个概率随着时间推移逐渐降低(逐渐降低才能趋向稳定)相当于上图中,从B移向BC之间的小波峰时,每次右移(即接受一个更糟糕值)的概率在逐渐降低。如果这个坡特别长,那么很有可能最终我们并不会翻过这个坡。如果它不太长,这很有可能会翻过它,这取决于衰减 t 值的设定。
Matlab程序:
%% I. 清空环境变量
clear all
clc
%% II. 导入城市位置数据
X = [16.4700 96.1000
16.4700 94.4400
20.0900 92.5400
22.3900 93.3700
25.2300 97.2400
22.0000 96.0500
20.4700 97.0200
17.2000 96.2900
16.3000 97.3800
14.0500 98.1200
16.5300 97.3800
21.5200 95.5900
19.4100 97.1300
20.0900 92.5500];
%% III. 计算距离矩阵
D = Distance(X); %计算距离矩阵
N = size(D,1); %城市的个数
%% IV. 初始化参数
T0 = 1e10; % 初始温度
Tend = 1e-30; %终止温度
L = 2; % 各温度下的迭代次数
q = 0.9; %降温速率
Time = ceil(double(solve([num2str(T0) '*(0.9)^x =',num2str(Tend)])));
% 计算迭代的次数
% Time = 132;
count = 0; %迭代计数
Obj = zeros(Time,1); %目标值矩阵初始化
track = zeros(Time,N); %每代的最优路线矩阵初始化
%% V. 随机产生一个初始路线
S1 = randperm(N);
DrawPath(S1,X)
disp('初始种群中的一个随机值:')
OutputPath(S1);
Rlength = PathLength(D,S1);
disp(['总距离:',num2str(Rlength)]);
%% VI. 迭代优化
while T0 > Tend
count =count + 1; %更新迭代次数
temp =zeros(L,N+1);
%%
% 1. 产生新解
S2 =NewAnswer(S1);
%%
% 2.Metropolis法则判断是否接受新解
[S1,R] =Metropolis(S1,S2,D,T0); %Metropolis 抽样算法
%%
% 3. 记录每次迭代过程的最优路线
if count ==1 || R < Obj(count-1)
Obj(count) =R; %如果当前温度下最优路程小于上一路程则记录当前路程
else
Obj(count) =Obj(count-1);%如果当前温度下最优路程大于上一路程则记录上一路程
end
track(count,:) = S1;
T0 = q *T0; %降温
end
%% VII. 优化过程迭代图
figure
plot(1:count,Obj)
xlabel('迭代次数')
ylabel('距离')
title('优化过程')
%% VIII. 绘制最优路径图
DrawPath(track(end,:),X)
%% IX. 输出最优解的路线和总距离
disp('最优解:')
S = track(end,:);
p = OutputPath(S);
disp(['总距离:',num2str(PathLength(D,S))]);
%%%%%%%%%%%%%%%%%%% Distance函数%%%%%%%%%%%%%%%%%%%%
function D = Distance(citys)
%% 计算两两城市之间的距离
% 输入 citys 各城市的位置坐标
% 输出 D 两两城市之间的距离
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
for j =i+1:n
D(i,j) =sqrt(sum((citys(i,:) - citys(j,:)).^2));
D(j,i) =D(i,j);
end
end
%%%%%%%%%%%%%%%%%%% DrawPath函数%%%%%%%%%%%%%%%%%%%%
function DrawPath(Route,citys)
%% 画路径函数
%输入
% Route 待画路径
% citys 各城市坐标位置
figure
plot([citys(Route,1);citys(Route(1),1)],...
[citys(Route,2);citys(Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
text(citys(i,1),citys(i,2),[' 'num2str(i)]);
end
text(citys(Route(1),1),citys(Route(1),2),' 起点');
text(citys(Route(end),1),citys(Route(end),2),' 终点');
%%%%%%%%%%%%%%%%%%% Metropolis函数%%%%%%%%%%%%%%%%%%%%
function [S,R] = Metropolis(S1,S2,D,T)
%% 输入
% S1: 当前解
% S2: 新解
% D: 距离矩阵(两两城市的之间的距离)
% T: 当前温度
%% 输出
% S: 下一个当前解
% R: 下一个当前解的路线距离
R1 = PathLength(D,S1); %计算路线长度
N = length(S1); %得到城市的个数
R2 = PathLength(D,S2); %计算路线长度
dC = R2 - R1; %计算能力之差
if dC < 0 %如果能力降低 接受新路线
S = S2;
R = R2;
elseif exp(-dC/T) >= rand %以exp(-dC/T)概率接受新路线
S = S2;
R = R2;
else %不接受新路线
S = S1;
R = R1;
End
%%%%%%%%%%%%%%%%%%% NewAnswer函数%%%%%%%%%%%%%%%%%%%%
function S2 = NewAnswer(S1)
%% 输入
% S1:当前解
%% 输出
% S2:新解
N = length(S1);
S2 = S1;
a = round(rand(1,2)*(N-1)+1); %产生两个随机位置 用来交换
W = S2(a(1));
S2(a(1)) = S2(a(2));
S2(a(2)) = W; %得到一个新路线
%%%%%%%%%%%%%%%%%%% OutputPath函数%%%%%%%%%%%%%%%%%%%%
function p = OutputPath(R)
%% 输出路径函数
% 输入:R 路径
R = [R,R(1)];
N = length(R);
p = num2str(R(1));
for i = 2:N
p =[p,'—>',num2str(R(i))];
end
disp(p)
%%%%%%%%%%%%%%%%%%% PathLength函数%%%%%%%%%%%%%%%%%%%%
function Length = PathLength(D,Route)
%% 计算各个体的路径长度
% 输入:
% D 两两城市之间的距离
% Route 个体的轨迹
Length = 0;
n = size(Route,2);
for i = 1:(n - 1)
Length =Length + D(Route(i),Route(i + 1));
end
Length = Length + D(Route(n),Route(1));









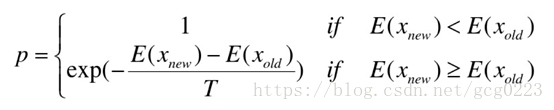













 7013
7013











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








