前言
Delta-Sigma ADC ,也有称为 Sigma-Delta ADC、ΔΣ ADC、ΣΔ ADC。
Delta-Sigma ADC 的应用非常广泛,特别是对于低频、高分辨率的信号处理场景,我们可能在不经意之间就使用到了 Delta-Sigma ADC,比如音频 Codec、生理监测、环境/过程控制,还有树莓派扩展板 “ADC Pi” 中的 MCP3424 也是一颗 Delta-Sigma ADC。
然而,相比于 SAR ADC, Delta-Sigma ADC 的工作原理有点令人费解,今天就尝试为大家介绍一下。
Delta-Sigma ADC 框图
在 TI 的应用笔记 “How delta-sigma ADCs work, Part 1” (详见参考资料 [1])中给出了这类 ADC 的框图:
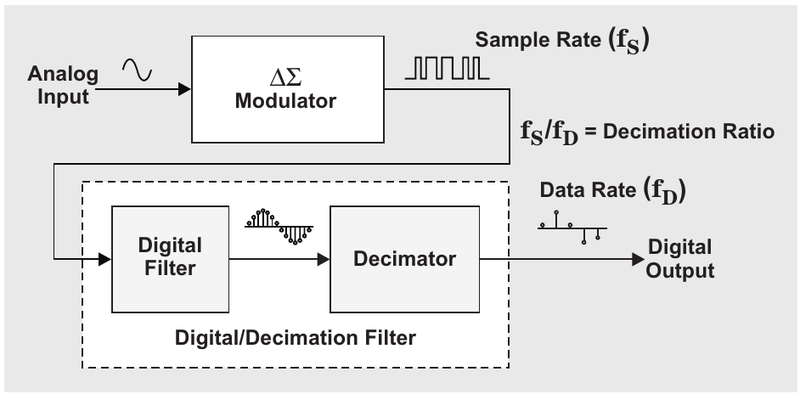
图1 Delta-Sigma ADC 框图,来源 [1]
它由两部分组成,ΔΣ 调制器 与 数字/抽取滤波器:
- ΔΣ 调制器:是一种调制器,将模拟信号调制成频率很高的 1 bit 数字信号,很多芯片手册里提到的 过采样(Oversampling)和 噪声整形(Noise shaping)就发生在这里。
- 数字/抽取滤波器:数字滤波器是为了去除目标信号以外的频谱成份,而抽取滤波器是为了将输出数据降低到合适的速率。
我们在此主要看 ΔΣ 调制器,因为它是这类 ADC 的基础。
ΔΣ 调制器
在 TI 文中提供了“1 bit 一阶 ΔΣ 调制器”的示意图,它由微分器(Difference Amplifier)、积分器(Integrator)、比较器(Comparator)、DAC 组成:
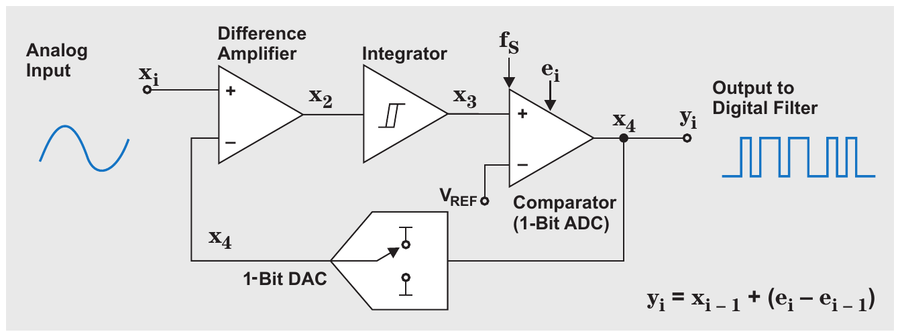
图2 一阶 ΔΣ 调制器,来源 [1]
其中:
- 对于 1 bit 的 ΔΣ 调制器,每次量化结果只有二进制 “1” 或 “0” 的 1 bit;
- DAC 也是 1 bit ,量化结果经 DAC 反馈到输入端,与输入信号相减,两者之差就是量化误差,体现的是 “Delta” 的部分;
- 积分器累积量化误差,因为是一阶的,只记录过去 1 个延时单位,累积后送到比较器,体现的是 “Sigma” 的部分;
- 比较器相当于 1 bit 的 ADC,如果量化误差大于参考值,输出二进制的 “1” ,反之输出二进制的 “0” 。
这套系统以高频时钟运作,多次的量化结果输出一连串的二进制码流,每个码的速率是固定的。
时域表示
我发现在 ADI 的一个在线教程中(详见参考资料 [2]),提供了上述系统运作的单步骤运作演示,你可以打开网页尝试一下,一步步点击“Next Step”查看结果,如下是 Vin = 1.0V 的例子截图:
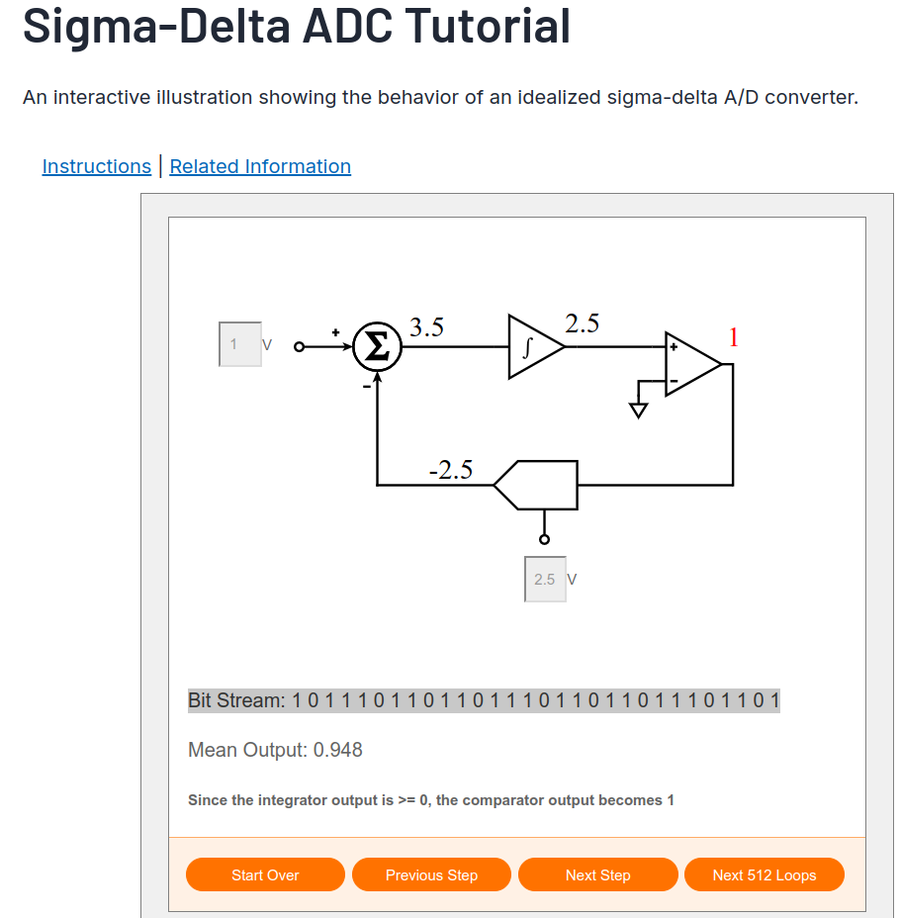
图3 ΔΣ 调制器 单步骤演示,来源 [2]
图中,DAC 的参考电压 Vref = 2.5V,当量化结果为 “1” 时,DAC = 2.5V;当量化结果为 “0” 时,DAC = -2.5V;这意味着输入信号的幅度范围可以是 -2.5V 至 +2.5V( +/- Vref )。
此时,对于输入信号 Vin = 1.0V ,显示了前 30 个量化结果,分别为:1、0、1、1、1、0、1、1、0、1、1、0、1、1、1、0、1、1、0、1、1、0、1、1、1、0、1、1、0、1。
那么,这些量化结果是如何表示 Vin 呢?
重点来了,是用密度。在上述 30 个量化结果中有 21 个 “1”,说明输入信号是满量程的 21/30 = 70%,即:-2.5 + ( 2.5 *2 ) * 70% = 1V 。注意,是从底部 -Vref 开始算起的。
又因为是纯粹数字化的步骤运算,很容易用 Excel 表格来模拟,比如以下是我用 Excel 模拟上述 Vin = 1.0V 的例子,前 30 个输出结果(Camparator Out 列)与网页是一致的,右侧的波形图分别是 Vin (蓝色波形)和 DAC 输出(橙色波形),并且,Excel 下侧的状态栏显示 Average 是 0.7 (字比较小):
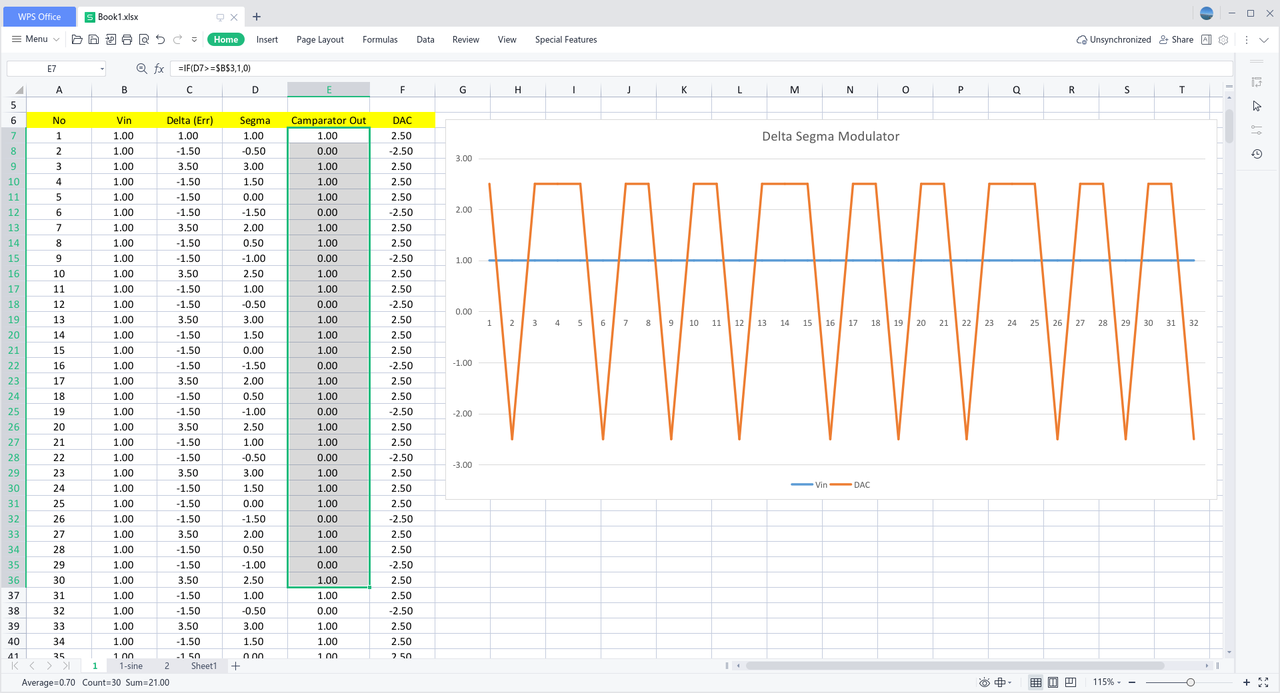
图4 Excel 模拟 ΔΣ 调制器过程,输入为直流信号
那么,如果将 Vin 改为正弦波,会得到怎么样的结果?
再次用 Excel 表格模拟如下,右侧波形图分别是 Vin (蓝色波形)和 DAC 输出(橙色波形):
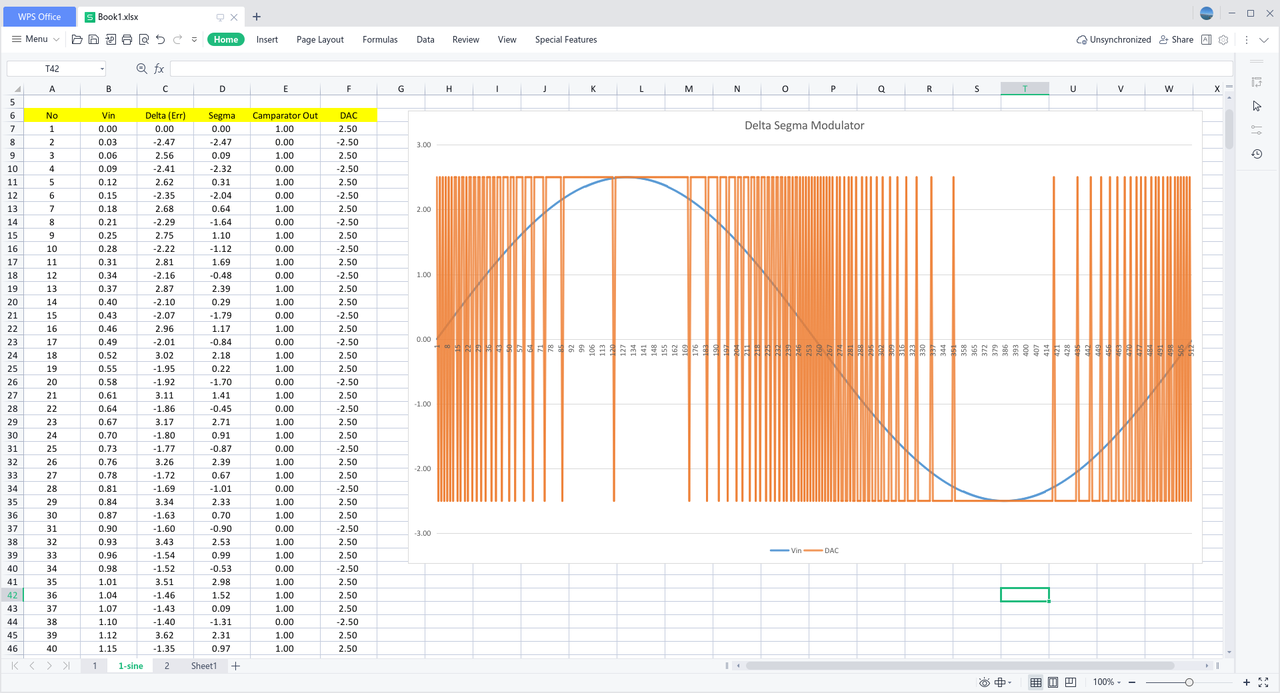
图5 Excel 模拟 ΔΣ 调制器过程,输入为正弦信号
可以看出,对于 1 bit 一阶 ΔΣ 调制器,它就像是 脉冲密度调制 PDM(Pulse Density Modulation),在输入信号的幅度越接近 +Vref 时,用越多 “1” 表示,在输入信号的幅度越接近 -Vref 时,用越多 “0” 表示。
WiKi百科上还列举了 这种“1 bit 一阶 ΔΣ 调制器” 的公式,推算出图2 中 Yi 与 Xi 的关系,以及 Python 代码实现,有兴趣可以参阅(详见参考资料 [3])。
频域表示
回到 TI 的文章(详见参考资料 [1])中,后续讲述的是这套 ΔΣ 调制器系统的频谱特性,它能将量化噪声的频谱成分推向高频区域:
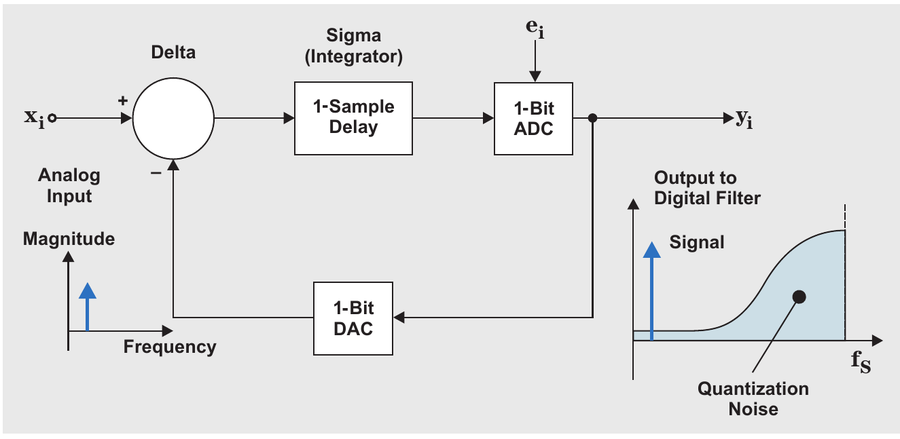
图6 ΔΣ 调制器的频谱特性,来源 [1]
并阐述了不同阶数情况下的转移函数,以及对应的频谱特性:
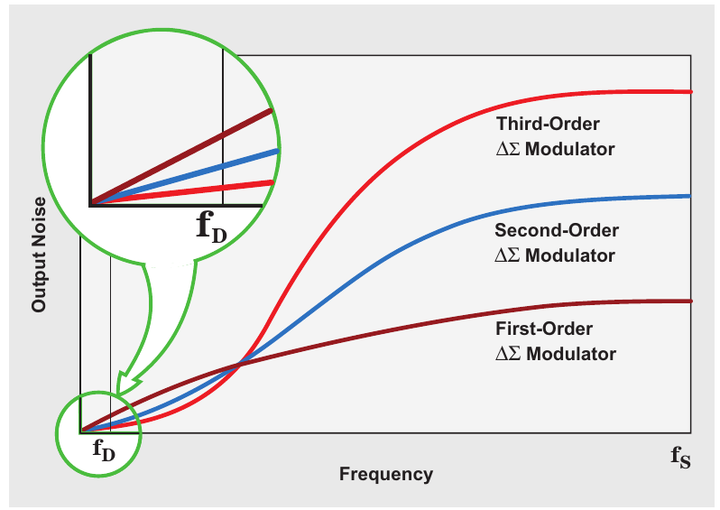
图7 ΔΣ 调制器不同阶数的频谱特性,来源 [1]
可以看到阶数越大(与过往更多数据有关),量化噪声越集中于高频区域,这就是所谓的噪声整形 Noise shaping。经过后续滤波,能过滤除噪声,有利于目标信号频谱区域内的信噪比。
小结
本文介绍了 Delta-Sigma ADC 中的 ΔΣ 调制器,通过 ADI 的在线演示(参考资料 [2])或自行编写 Excel 能够模拟 “1 bit 一阶 ΔΣ 调制器” 的运作过程,对于这种调制器,其量化结果与 PDM 脉冲密度调制 类似(参考资料 [3])。
关于 Delta-Sigma ADC 的详细介绍,可以查看 TI 的 slyt423a 和 slyt438(参考资料 [1] 和 [4]),其中讲述了过采样、噪声整形、数字/抽样滤波等内容。
参考资料
参考资料均可以通过搜索关键词获取,查阅原文:
- slyt423a: How delta-sigma ADCs work, Part 1
- https://www.analog.com/en/resources/interactive-design-tools/sigma-delta-adc-tutorial.html
- https://en.wikipedia.org/wiki/Pulse-density_modulation
- slyt438: How delta-sigma ADCs work, Part 2
欢迎关注我的微信公众号“疯狂的运放”,及时收到最新的推文。

























 895
895

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










