Linear regression with one variable
同样以上个例子中房价为例,有一组房子面积与房价所对应额数据如下所示
图-1 图片来自吴恩达“机器学习”
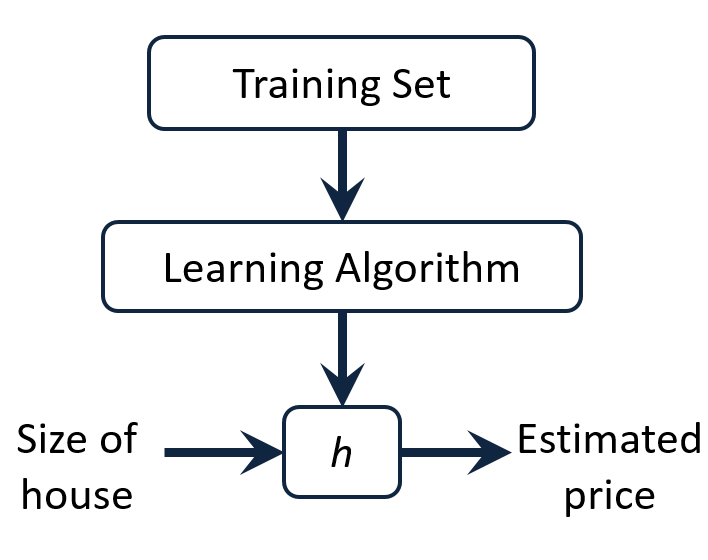
首先约定m代表数据集的大小,x代表输入,y代表输出。线性回归可以看做输出可以表示为输入元素的线性组合。那么线性回归过程可以理解为从训练数据集中通过学习算法,求解出这一线性组合,使得任意给定的输入x都能够通过该组合求解出对应的y。这一过程用图示可以表示为
图-2 图片来自吴恩达“机器学习”
按照之前所述,h即为要学习出的模型,它表示为输入元素的线性的组合,当只有一个输入变量时,表达式可以表述为
所以Learning Algorithm中要求解的便是变量所对应的参数,那么应该怎么求解呢?
Cost function
最理想的情况下对于任意的输入x都有h(x)=y,那么这样对于数据集的描述便是最为贴切的。但是现实中这种情况几乎不会出现,所以定义代价函数(cost function)为h(x)与y的差的平方和再乘以一个常数,当代价函数最小时便表示h(x)对于数据集的描述最为贴切。此例中代价函数定义为
显然要求解合适的参数就只要让该代价函数取得最小值即可。
至此完整的含有一个变量的线性回归模型可以表述为
Gradient descent
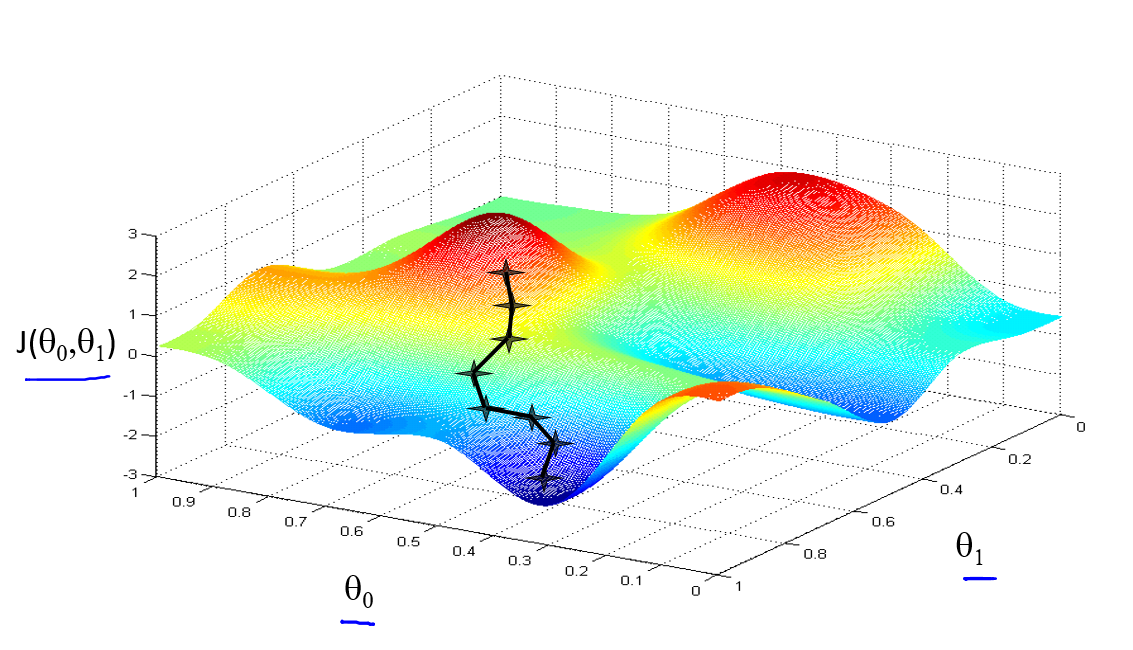
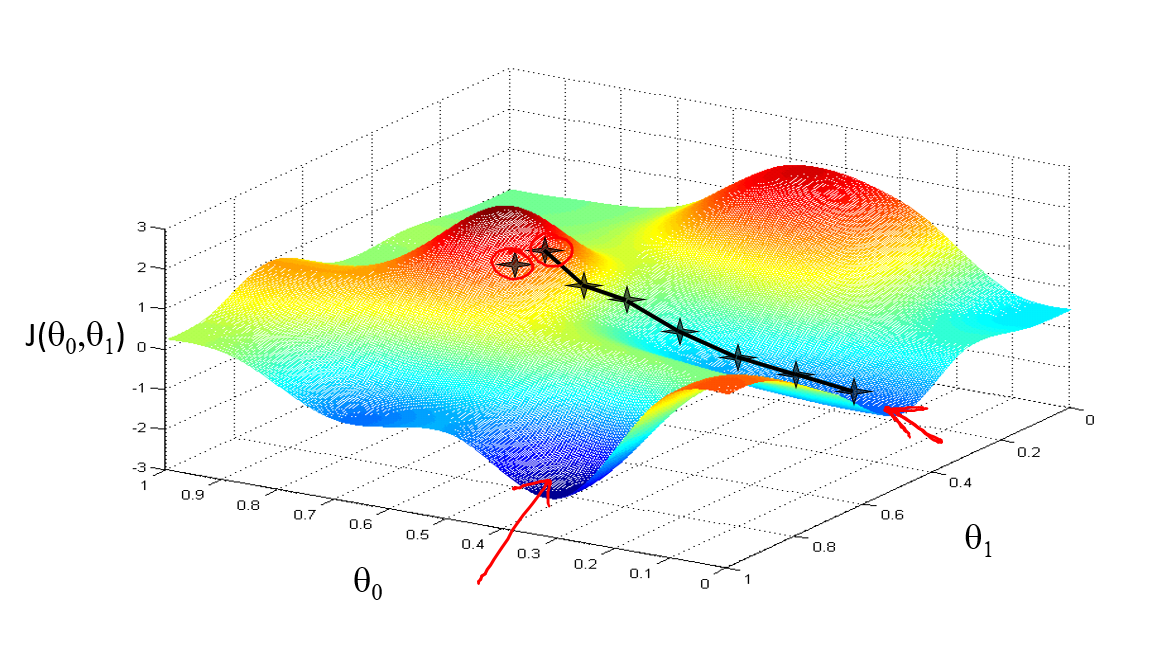
Gradient descent(梯度下降法)常用于求解函数的最小值,它的基本步骤是取任意的开始点,然后不断地同时改变参数,直到函数取得最小值为止。这么说可能感觉有点莫名其妙,换一个形象一点的说法,站在山坡上,想要以最快的速度到达山底,先环顾四周,找一个最陡的方向向下迈出一步,然后再重复上述过程直到到达山的底部。细心的人可能从这个描述中就可以看出来,梯度下降法求解的是局部的最优解。一个形象的图示可以表达为
可以看到起始点的微小差异导致了完全不同的结果。对于线性回归来说,其函数总是凸的,也就是不存在有多个局部最优解的情况,所以利用梯度下降法求解得到的即为其全局最优。
那么哪个方向才是最陡的呢,学过微积分的人应该能很容易给出答案,即其导数的方向,所以Gradient descent的数学表达式可以表述为
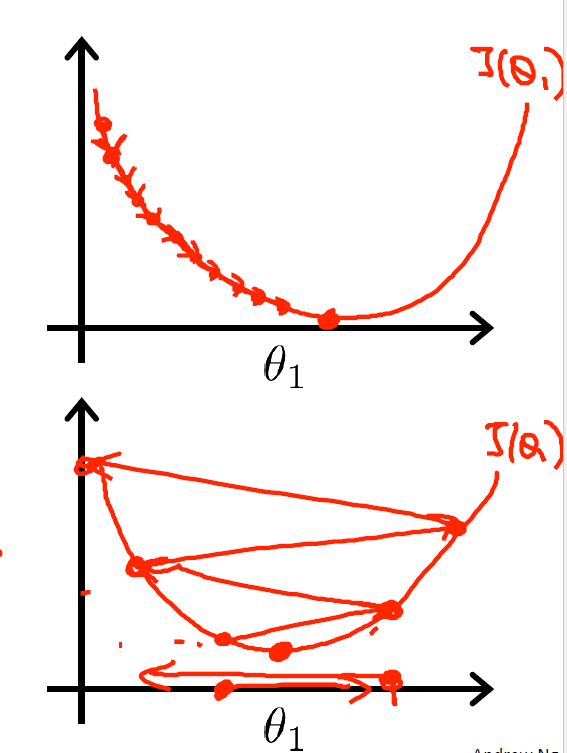
:=符号表示的是赋值符号,即将变量q每次改变a乘以函数对q的偏导,注意的是有多个变量的时候应该同时改变它们。其中a称为步长,尤为重要。如果步长太小会导致求解最小值的过程异常缓慢而步长太大则可能导致最后得不到理想的结果。
上图分别对应于步长太小与步长太大的情况,步长太大的危害尤为需要注意,因为可能会导致函数每次迈过了最低点,使得想要求解的函数值越来越大,最终变得莫名其妙起来。
对于线性回归来说,将代价函数代入进去,即可得到
注意的是应该同时改变两个参数的值。可以看到上式中每次改变都涉及到了所有的样本参数,这种叫做Batch gradient descent.
Linear regression with multiple variables
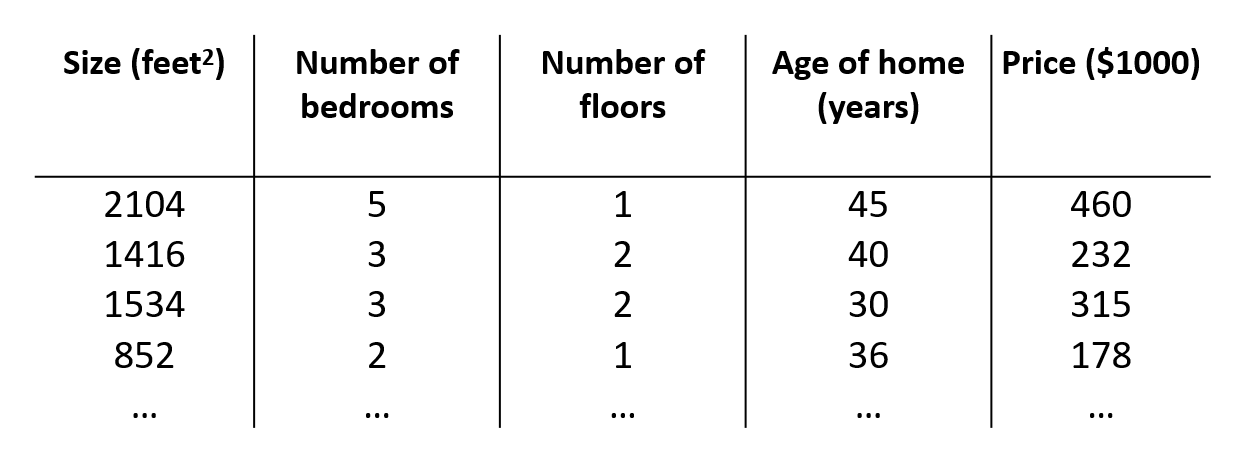
还是房价的例子,不过这回增加了几个变量如下所示
同理定义m为样本的个数,n为特征点个数,对于x用下标表示是其第几个特征。那么得到新的h(x)为
令x0=1,便可以将上式表达为矩阵相乘的形式。此时将要求解的参数的个数为n,对应的代价函数为
将代价函数代入梯度下降中去,即为
求解方法并没有什么不同。
Feature scaling & Mean normalization
在gradient descent的求解中会用到很多技巧加快求解过程。Feature scaling的思想是尽量使得特征位于相同的尺度内,一般来说将每个特征点都变换到-1到1之间最为合适。这可以通过将feature与其变换范围相除来得到;而Mean normalization指的是尽量让feature的平均数接近于0,这可以通过将feature减去其平均数得到。
Normal equation
对于线性回归来说,还有另外一种方法可以求解代价函数的最小化,即令其代价函数的偏导等于0即可求出。
一般来说当数据特征n不是很大的时候可以采用此方法来求解线性回归的代价函数最小化,而当n较大的时候还是梯度下降法效率较高。








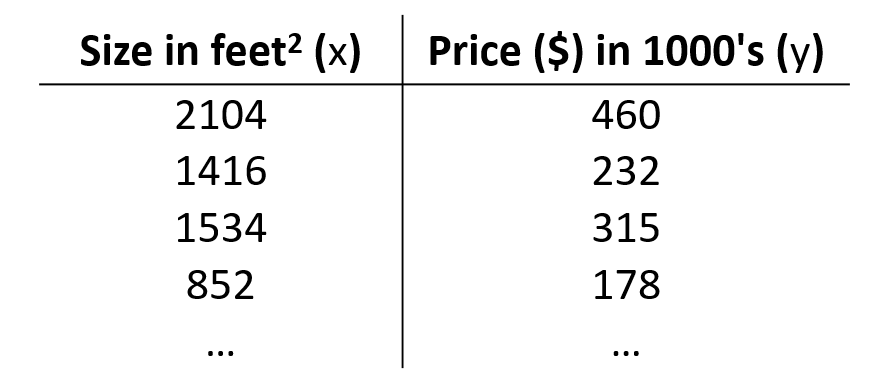
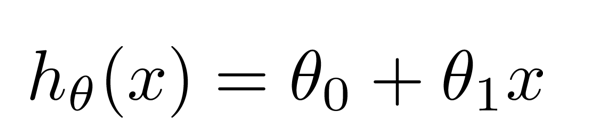
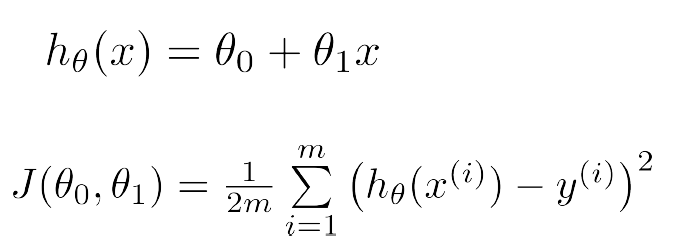
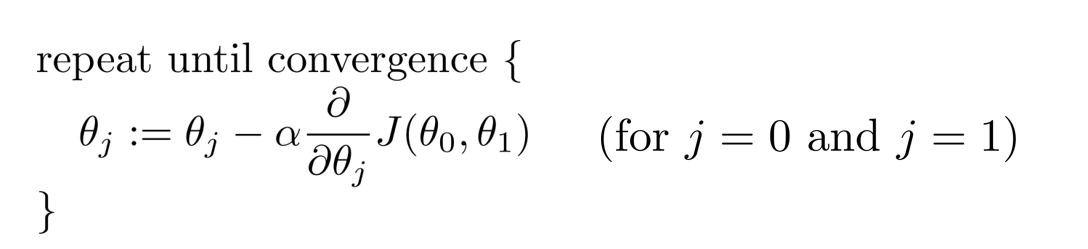
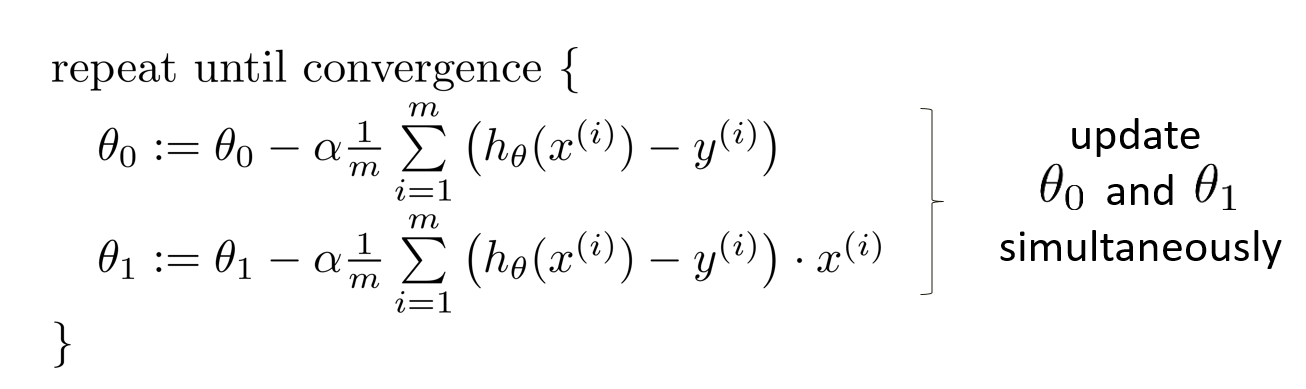

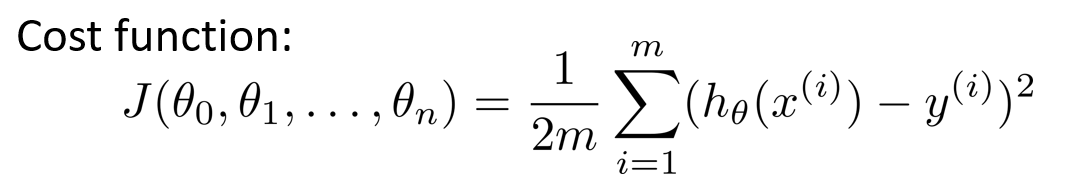

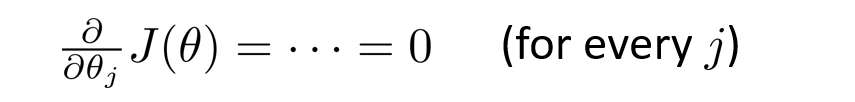














 8711
8711

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








