一、BFGS算法简介
BFGS算法是使用较多的一种拟牛顿方法,是由Broyden,Fletcher,Goldfarb,Shanno四个人分别提出的,故称为BFGS校正。
同DFP校正的推导公式一样,DFP校正见博文“
优化算法——拟牛顿法之DFP算法”。对于拟牛顿方程:
可以化简为:
令
 ,则可得:
,则可得:
在BFGS校正方法中,假设:
二、BFGS校正公式的推导
令
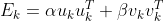 ,其中
,其中
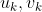 均为
均为
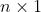 的向量。
的向量。
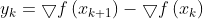 ,
,
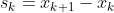 。
。
则对于拟牛顿方程
 可以化简为:
可以化简为:
将
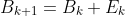 代入上式:
代入上式:
将
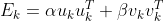 代入上式:
代入上式:
已知:
 为实数,
为实数,
 为
为
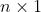 的向量。上式中,参数
的向量。上式中,参数
 和
和
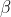 解的可能性有很多,我们取特殊的情况,假设
解的可能性有很多,我们取特殊的情况,假设
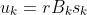 ,
,
 。则
。则
代入上式:
令
 ,
,
 ,则:
,则:
则最终的BFGS校正公式为:
三、BFGS校正的算法流程
设
 对称正定,
对称正定,
 由上述的BFGS校正公式确定,那么
由上述的BFGS校正公式确定,那么
 对称正定的充要条件是
对称正定的充要条件是
 。
。
在博文“
优化算法——牛顿法(Newton Method)”中介绍了非精确的线搜索准则:Armijo搜索准则,搜索准则的目的是为了帮助我们确定学习率,还有其他的一些准则,如Wolfe准则以及精确线搜索等。在利用Armijo搜索准则时并不是都满足上述的充要条件,此时可以对BFGS校正公式做些许改变:
BFGS拟牛顿法的算法流程:

四、求解具体优化问题
求解无约束优化问题
其中,
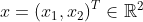 。
。
python程序实现:
- function.py
#coding:UTF-8 ''' Created on 2015年5月19日 @author: zhaozhiyong ''' from numpy import * #fun def fun(x): return 100 * (x[0,0] ** 2 - x[1,0]) ** 2 + (x[0,0] - 1) ** 2 #gfun def gfun(x): result = zeros((2, 1)) result[0, 0] = 400 * x[0,0] * (x[0,0] ** 2 - x[1,0]) + 2 * (x[0,0] - 1) result[1, 0] = -200 * (x[0,0] ** 2 - x[1,0]) return result - bfgs.py
#coding:UTF-8 from numpy import * from function import * def bfgs(fun, gfun, x0): result = [] maxk = 500 rho = 0.55 sigma = 0.4 m = shape(x0)[0] Bk = eye(m) k = 0 while (k < maxk): gk = mat(gfun(x0))#计算梯度 dk = mat(-linalg.solve(Bk, gk)) m = 0 mk = 0 while (m < 20): newf = fun(x0 + rho ** m * dk) oldf = fun(x0) if (newf < oldf + sigma * (rho ** m) * (gk.T * dk)[0,0]): mk = m break m = m + 1 #BFGS校正 x = x0 + rho ** mk * dk sk = x - x0 yk = gfun(x) - gk if (yk.T * sk > 0): Bk = Bk - (Bk * sk * sk.T * Bk) / (sk.T * Bk * sk) + (yk * yk.T) / (yk.T * sk) k = k + 1 x0 = x result.append(fun(x0)) return result - testBFGS.py
#coding:UTF-8 ''' Created on 2015年5月19日 @author: zhaozhiyong ''' from bfgs import * import matplotlib.pyplot as plt x0 = mat([[-1.2], [1]]) result = bfgs(fun, gfun, x0) n = len(result) ax = plt.figure().add_subplot(111) x = arange(0, n, 1) y = result ax.plot(x,y) plt.show()
五、实验结果






 本文深入探讨了BFGS算法的原理及其在优化问题中的应用,并提供了基于Python的实现示例。
本文深入探讨了BFGS算法的原理及其在优化问题中的应用,并提供了基于Python的实现示例。
















 8432
8432

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








