MPDM:面向自动驾驶的动态、不确定环境中的多策略决策
摘要
城市交通中的真实世界自动驾驶必须应对包含具有不确定意图的其他智能体的动态环境。这带来了一个具有挑战性的决策问题,例如,决定何时执行超车操作或如何安全地并入车流。现有文献中的研究通常采用特设性方法解决该问题,未考虑其他智能体的可能未来状态,因此在扩展到复杂交通场景时存在困难,尤其是在各参与智能体的行为相互紧密依赖的情况下。本文提出多策略决策(MPDM),这是一种利用自动驾驶领域知识,在线为行驶在交通环境中的自动驾驶汽车做出决策的算法。该算法假设受控车辆和其他交通参与者在每个时间步均从一组合理的闭环策略中选择一个策略执行,并据此为受控车辆选择最优可用策略。我们通过前向仿真受控车辆及其他智能体的行为,高效地采样其交互过程中的高可能性结果,进行策略选择。随后,使用用户定义的成本函数对产生的结果进行评分,以适应不同的驾驶偏好,并选择得分最高的策略。我们在真实自动驾驶汽车执行超车操作以及模拟合流场景中验证了该算法的有效性。
一、引言
在过去的十年中,人们在开发能够在城市交通中运行的全自动驾驶汽车方面开展了大量工作。通过早期的美国国防高级研究计划局挑战赛和城市挑战赛,对鲁棒性自动驾驶问题进行了研究,自那以后,许多团队一直在积极开发更先进的能力。在路径规划、多传感器感知和数据融合等领域的研究,使得车辆能够穿越复杂环境,并应对障碍物和其他危险的存在。
能够在真实世界环境中稳健运行的自动驾驶汽车面临的一个关键挑战是离散不确定性,即在选择动作时需要考虑环境中其他智能体的意图。这些智能体包括道路上的其他驾驶员,以及人行横道和停车场中的行人。人类驾驶员所做的许多决策都是针对离散动作的,例如决定是否变换车道或是否驶入交通流中。这些决策必须同时基于状态的连续不确定性(例如车辆的实际位置)以及离散不确定性(例如另一位驾驶员是否正在转弯,或试图超越另一辆车辆)。
直接处理这种离散不确定性至关重要,因为在交通环境中操作汽车所需应对的广泛行为使得传统技术(如手工调整的有限状态机(FSM)[1]或轨迹优化[2])难以扩展到完整的实际驾驶场景。这类技术的一个主要缺点是无法对多个智能体之间的交互进行建模,而这一点对于在动态交通环境中高效且安全地导航至关重要。
相比之下,本文提出了一种多策略决策(MPDM)方法,这是一种将自动驾驶分解为一系列策略的高层决策过程,这些策略编码了闭环行为,并通过在线仿真来评估可用策略的结果。本文的主要贡献在于:
- 一种能够处理交通的决策算法。
- 该技术利用对闭环交互的仿真来推理动作后果。
- 在仿真环境和真实世界自动驾驶车辆中对MPDM进行评估,场景包括超车和汇流交通。
将车辆行为建模为闭环策略,用于控制我们自身的车辆和附近车辆,可实现管理通过假设其他车辆将做出合理、安全的决策来抑制不确定性增长。在环境中对其他车辆进行前向仿真,使我们能够考虑邻近车辆引起的驾驶员行为变化,例如在汇流场景中,另一名驾驶员会减速以腾出空间让汇流车辆进入(见图1)。
在此方法中,策略是闭环确定性控制器,用于实现高层驾驶行为,例如沿车道行驶、变道或停车。为了选择最优策略,针对每个候选策略,我们通过前向仿真车辆状态以及其他交通参与者的未来动作,从当前世界状态中采样策略结果。然后,我们可以对这些采样结果评估奖励函数,以满足用户驾驶偏好,例如快速到达目标和乘坐舒适性。我们在真实世界自动驾驶汽车执行超车操作以及模拟车道汇入场景中验证了该算法。
此外,我们以部分可观测马尔可夫决策过程(POMDP)模型为基础,系统化地构建我们的方法(参见[3]获取教程),因为该模型为同时考虑最优性准则和动态环境中的固有不确定性提供了一个强大的框架。然而,对于通用POMDPs而言,在连续状态和动作域中寻找最优解是难解的[4],[5],。尽管如此,我们将使用POMDP作为形式化模型,以明确指出近似和假设的引入之处。
II. 相关工作
最显著的早期自动驾驶汽车决策架构实例源自2007年DARPA城市挑战赛[6], ,这是一场在模拟城市环境中举行的自动驾驶汽车比赛。如前所述,美国国防高级研究计划局的参赛者采用了多种解决方案来应对决策问题,包括有限状态机[1]、决策树[7]以及启发式方法[8]。然而,这些方法仅适用于特定且简化的场景,无法“适应多样化的真实世界”[8]。
许多研究人员通过轨迹优化的视角来解决自动驾驶中的决策问题。陈和迪尔提出了一种凸优化方法,并将其应用于仿真中的自动化类车车辆[9]。然而,他们的方法未考虑环境中的动态物体。顾和多兰使用动态规划生成轨迹,该方法考虑了环境中动态物体的影响[10]。尽管他们的仿真结果令人鼓舞,但他们并未在实车上验证该方法。文献[2]中提出的轨迹优化方法优化了一组代价,旨在最大化路径效率和舒适性,同时考虑与静态和动态障碍物的距离。他们在简单超车操作中验证了该方法,但其实车结果仅限于静态障碍物。在交通场景中进行轨迹优化的关键问题是,这些方法仅考虑其他车辆当前的位置,而未能充分预测其未来的行驶状态。可能无法考虑到车辆在未来会采取的动作,特别是对我方车辆行为的响应。
部分可观测马尔可夫决策过程为自动驾驶等动态不确定场景中的决策问题提供了严谨的数学建模方法。现有文献中存在多种通用的POMDP求解器,旨在逼近该问题的解,例如[11],[12]。然而,即使对于状态、动作和观测空间非常小的问题,这些方法所需的计算时间也长达数小时,与现实场景相比仍不实用。在POMDP相关研究中,与本文方法存在一定相似性的工作见于[13],,其中提出了一种利用领域知识(表示为一组预计算的初始策略)的POMDP求解器,并在运行过程中对这些策略进行优化并动态切换。但该方法应用于实际系统时仍需要过长的计算时间。事实上,假设采用有限策略集以加快规划速度的思想此前已有研究,特别是在POMDP文献中[14]–[16]。然而,这些方法需耗费大量资源来计算其策略集合,因而仅限于较短的规划时域以及相对较小的状态、观测和动作空间。相比之下,我们提出利用自动驾驶领域的领域知识,设计一组在规划时刻即可直接使用的策略。
弗达和弗拉契奇采用了一种更实用的方法,通过使用多准则决策理论(MCDM)对自动驾驶汽车的决策过程进行形式化处理[17]。然而,他们并未明确考虑其他交通参与者未来的潜在意图。最近,魏等人提出了一种两步决策方法,通过评估一组候选动作来找到合适的速度曲线[18]。尽管如此,该方法主要针对车道内驾驶情况,并未考虑超车或并道等复杂决策。在早期的研究中,魏等人对高速公路匝道上车辆之间的交互进行了建模,以执行汇流操作[19]。然而,其结果仅限于仿真。类似地,特劳特曼等人探讨了对其他智能体的交互建模用于规划[20],,并展示了移动机器人在拥挤的室内环境中导航的评估结果。
总体而言,现有研究在智能体之间存在广泛耦合交互的场景中,仍缺乏稳健的原则性决策方法。本研究通过建模系统中所有智能体的高层行为,直接解决了这一问题。
III. 问题描述
在多个智能体行为紧密耦合的动态、不确定环境中进行决策的问题可以被建模为POMDP,该模型提供了一种将感知与规划以原则性方式连接起来的数学框架。本文首先将该问题表述为一个通用的多智能体POMDP,然后利用此表述说明我们在方法中通过合理的领域假设进行近似的位置,从而实现一种能够在线控制自动驾驶汽车在多智能体环境中导航的决策系统。
A. 通用决策过程公式化
令 $v \in V$ 表示局部区域内的 $N$ 辆车辆之一,包括我们的受控车辆,我们可以为其定义一个动作 $a_t^v \in A$,该动作将其在时间 $t$ 的状态 $x_t^v \in X$ 转换为新状态 $x_{t+1}^v$。动作 $a_t^v$ 是我们车辆在转向、油门、刹车、换挡器和转向灯上的执行控制组成的元组。需要注意的是,为了可靠地控制车辆,有必要以相对较高的频率(约为30到50赫兹)选择这种细粒度的动作。为了记法上的方便,令 $x_t$ 表示所有车辆的状态变量集合,相应地令 $a_t$ 表示所有车辆的行为。
为了对系统中的动态性和不确定性进行建模,我们采用马尔可夫模型根据动力学、观测和驾驶员行为模型来推进系统的演化。条件概率函数 $T(x_t, a_t, x_{t+1}) = p(x_{t+1}|x_t, a_t)$ 用于建模动作对车辆状态的影响。同样地,我们将观测不确定性建模为条件概率函数 $Z(x_t, z_t^v) = p(z_t^v |x_t)$,其中 $z_t \in Z$ 是在每个时间点 $t$ 的传感器观测的集合,包括观测到的车辆状态以及环境中静态危险物地图。此外,我们将环境中其他智能体的行为建模为条件概率分布 $D(x_t, z_t^v |z_t^v, x_t)$,其中驾驶员所采取的动作仅依赖于当前状态和观测。
我们在此决策过程中希望解决的核心问题是为我方车辆选择一个最优策略 $\pi^
$,其中车辆的策略是一种确定性映射 $\pi^v: x_t \times z_t^v \rightarrow a_t^v$,该映射根据当前状态和观测生成一个动作。决策过程选择该策略以在给定的决策范围 $H$ 内最大化奖励,具体如下:
$$
\pi^
= \arg\max_\pi \sum_{t=0}^H \gamma^t \int_{x_t} R(x_t)p(x_t) dx_t, \quad (1)
$$
其中 $\gamma^t$ 是奖励折扣因子,$R(x_t)$ 是奖励函数。我们可以如下定义联合密度 $p(x_t)$:
$$
p(x_{t+1}) = \iiint_{x_t z_t a_t} p(x_{t+1}, x_t, a_t, x_t) da_t dz_t dx_t \quad (2)
$$
并使用上述状态转移、观测和驾驶员行为模型进行递归分解得到
$$
p(x_{t+1}) = \iiint_{x_t z_t a_t} p(x_{t+1}|x_t, a_t)p(a_t| z_t, x_t) p(z_t |x_t)p(x_t) da_t dz_t dx_t . \quad (3)
$$
鉴于这是一个多车辆系统,我们可以假设每辆车的瞬时动作彼此独立,因为动作 $a_t^v$ 仅依赖于当前状态 $x_t$ 和局部观测 $z_t^v$。设单个车辆 $v$ 的联合密度为
$$
p_v(x_t^v, x_{t+1}^v, z_t^v, a_t^v) = p(x_{t+1}^v|x_t^v, a_t^v)p(a_t^v |x_t^v, z_t^v) p(z_t^v |x_t^v)p(x_t^v). \quad (4)
$$
利用独立性假设,我们得到
$$
p(x_{t+1}) = \prod_{v \in V} \iiint_{x_t z_t a_t} p_v(x_t^v, x_{t+1}^v, z_t^v, a_t^v) da_t^v dz_t^v dx_t^v. \quad (5)
$$
为了将确定性策略 $\pi_q$ 应用于受我们控制的车辆 $q \in V$,我们可以替换公式4中定义的单车联合决策中的驾驶员行为模型。在此模型构建完成后,我们可以通过从公式5的完整系统模型中采样,并在整个决策范围 $H$ 内进行传播,来估计给定策略 $\pi_q$ 的期望奖励。
这种公式化方法的问题在于,在从公式5的分布中进行采样时,由于每一阶段都存在不确定性,加之系统的状态空间庞大,每个样本的后验概率都会非常小。大的状态空间伴随着多层不确定性,导致组合爆炸,特别是当我们考虑其他车辆可能采取的所有可能动作序列时。
在实际驾驶场景中,我们希望对高可能性的情景进行采样,以支持决策。如果在整个模型上进行采样,将会出现许多其他驾驶员行为与人类驾驶员行为显著不同的情况,包括偏离道路和进入其他车道。然而,我们希望在模型中涵盖绝大多数驾驶场景,即所有驾驶员大多数时候都是安全的,以便我们能够预测其他车辆的可能行为。下一节将应用一些近似方法,旨在将采样集中在更可能发生的结果上。
B. 近似决策过程
在本节中,我们将介绍两个关键的近似方法,这些方法足以将状态空间缩减到可实时处理的程度:1)为我们的车辆和其他车辆从一组有限的已知策略中选择策略;2)通过对所有车辆进行确定性闭环前向仿真,并赋予其相应策略,来近似车辆动力学和观测模型。这些近似的最终结果是将寻找策略的问题转化为针对高层车辆行为的离散决策问题。
设 $\Pi$ 为一组精心构建的离散策略,其中每个策略描述一种特定的高层行为,例如沿车道行驶或进行变道。由于我们假设道路上的其他车辆遵循基本的驾驶规则,因此也可以选择一个策略 $\pi_t^v \in \Pi$ 来建模它们的行为。于是,我们可以将公式4中的每辆车联合分布重构为
$$
p_v(x_t^v, x_{t+1}^v, z_t^v, a_t^v, \pi_t^v) = p(x_{t+1}^v|x_t^v, a_t^v)p(a_t^v |x_t^v, z_t^v, \pi_t^v) p(\pi_t^v |x_t^v)p(z_t^v |x_t^v)p(x_t^v), \quad (6)
$$
其中,我们将驾驶员行为项 $p(a_t^v |x_t^v, z_t^v, \pi_t^v)$ 在给定 $\pi_t^v$ 的情况下近似为确定性的。附加的项 $p(\pi_t^v |x_t^v)$ 建模了给定策略被选择用于该车辆的概率。本文假设在已知道路网络模型的情况下,我们可以确定其他车辆最可能的策略 $\pi_t^v$,并专注于我方车辆的控制。我们将在未来工作中解决 $p(\pi_t^v |x_t^v)$ 的精确计算问题。
使用公式6中单车联合分布的表述,我们最终将其他车辆 $v \in V$ 和我们控制下的车辆 $q \in V$ 分别拆分如下:
$$
p(x_{t+1}) \approx \iint_{x_q z_q} p_q(x_t^q, x_{t+1}^q, z_t^q, a_t^q, \pi_t^q) dz_t^q dx_t^q \prod_{v \in V|v \neq q} \left[\sum_\Pi \iint_{x_v z_v} p_v(x_t^v, x_{t+1}^v, z_t^v, a_t^v, \pi_t^v) dz_t^v dx_t^v \right]. \quad (7)
$$
通过将策略建模为闭环系统,我们可以利用系统动力学的确定性仿真,合理地近似公式6中的状态转移项 $p(x_{t+1}^v|x_t^v,a_t^v)$。这一近似是合理的,因为我们假设所有策略都经过工程设计,能够生成在车辆安全性能包络内可实现的动作序列,从而降低了不可控车辆动力学的影响。
IV. 多策略决策
我们提出的算法MPDM(算法1)利用确定性仿真来近似实现第III-B节中的近似决策过程,以模拟我方车辆和附近车辆的闭环策略执行。关键在于假设环境中智能体所执行的动作可以被建模为一组基于自动驾驶领域知识设计的策略,从而高效地逼近第III节所述问题的解。
MPDM通过对离散决策层面的持续重规划以及对底层控制层的闭环策略模型,能够有效应对未来的不确定性。与模型预测控制技术类似,通过在较长的时间范围 $H$ 内进行持续重规划,而仅在较短范围内执行,使我们能够响应变化的车辆行为。闭环策略模型确保了对状态估计和执行过程中有界底层不确定性的鲁棒性,因为这些策略可以适应局部扰动。
该算法以一组候选策略 $\Pi$、对当前世界状态 $p(x_0)$ 的当前最可能估计以及决策时域 $H$ 作为输入。需要注意的是,对世界状态的估计包括其他智能体当前正在执行的最可能策略,本文中我们根据道路网络模型及智能体在其中的位姿来确定这些策略。接着,算法会根据 $x_0$ 确定在当前世界状态下适用的一组策略 $\Pi_a$。算法的下一步是通过前向仿真,根据用户定义的成本函数对每条策略进行评分。在此步骤中,对于每条适用的策略 $\pi$,我们从状态 $x_0$ 下在 $\pi$ 作用下的系统演化进行采样,以获得一个状态序列


MPDM:面向自动驾驶的动态、不确定环境中的多策略决策
算法1:MPDM 策略选举过程
- 输入:
- 我方车辆及其他车辆的可用策略集合 $\Pi$
- 在规划时刻的状态最可能估计 $x_0$,包括其他车辆的最可能策略 $\pi_0^v \in \Pi$
- 规划时域 $H$
- $\Pi_a \leftarrow \emptyset$
- 对每个 $\pi \in \Pi$ 执行
- 如果 APPLICABLE($\pi, x_0$) 成立则
- $\Pi_a \leftarrow \Pi_a \cup {\pi}$
- $C \leftarrow \emptyset$
- 对每个 $\pi \in \Pi_a$ 执行
- $\Psi \leftarrow$ SIMULATE_FORWARD($x_0, \pi, H$)
- $c \leftarrow$ COMPUTE_SCORE($\Psi$)
- $C \leftarrow C \cup {\langle \pi, c \rangle}$
- $\pi^* \leftarrow$ SELECT_BEST($C$)
- 返回 $\pi^*$
世界 $\Psi = (x_0, x_1, …, x_H)$,其中 $x_t = \pi(x_{t-1}, z_{t-1})$ 对于 $0 < t \leq H$。接下来,使用用户定义的成本函数对序列 $\Psi$ 进行评分。得到的分数 $c$ 被添加到分数集合 $C$ 中。最后,返回与 $C$ 中最高分相关联的最优策略 $\pi^*$。
A. 策略设计
每个策略实现一种特定的闭环驾驶行为,例如沿车道行驶、变道或执行泊车操作。在运行时,我们在与策略选举过程分离的独立进程中执行当前选定的策略。这些策略经过单独设计,以应对特定的驾驶行为,复杂程度各不相同。例如,在一个简单的驾驶场景中,策略可以是:
-
保持车道
:在当前车道内行驶,并与正前方车辆保持距离,
-
向左变道 / 向右变道
:每个方向的单个变道动作分别对应一个独立的策略,
-
泊车
:在标线停车位内停车。
该策略集合的构建主要依赖于涵盖导航给定道路网络和遵守交通规则所需的行为集合。我们可以调整所表示行为范围以匹配特定应用,例如将车辆限制在仅高速公路行驶的行为。
在任何给定的世界状态 $x_t$ 下,可能只有一部分车辆行为是可执行的,因此我们首先对每个可用策略运行一个 applicability 检查。例如,如果我们的车辆处于高速公路的最右侧车道,则向右变道的策略将不可执行。
请注意,算法1中详述的策略选择过程在实际应用中运行速度不够快,无法应对紧急车辆处理或突发变化系统状态,因此所有策略都被设计为始终产生安全动作。这一约束确保我们能够以实时速度响应变化的环境,而不受策略选择速度的限制。该安全标准对于管理其他车辆的异常策略(相对于 $p(\pi_t^v |x_t^v)$)至关重要,在这些情况下,我们允许各自的策略处理危险情形。在未来工作中,我们将扩展针对其他车辆的策略集,以包含更多易于建模的异常情况,例如停车。
B. 多车仿真
通过将前向仿真视为一个闭环确定性系统,我们可以捕捉车辆之间的必要交互,从而为我方车辆行为做出合理选择。我们为环境中每辆其他车辆选择一种可能的策略,然后通过公式7中详细描述的确定性状态转移模型进行推进。
为了以1赫兹或更快的实时速率实现策略选择,我们依赖底层控制的闭环特性来实现近似仿真。虽然可以进行高保真仿真,但在实践中,我们为每辆车辆采用假设理想转向控制的简化仿真模型。关键在于,该仿真模型能够充分模拟车与车之间的交互,从而对执行哪个策略做出合理决策。
C. 策略选择
为了选择要遵循的策略,我们需要使用包含多种用户定义的指标的成本函数来评估每种候选策略在仿真中的结果,然后选择最佳策略。该问题的难点在于如何兼顾现实世界驾驶决策中涉及的众多标准。自动驾驶汽车不仅需要以及时的方式到达目的地,同时还必须以确保乘客舒适、遵守驾驶规则并保持安全的方式行驶。
我们将这些标准表述为一组度量指标 $m \in M$,其中每个度量指标是一个函数 $m : {x_t} \to \mathbb{R}$,用于评估在固定时间范围 $H$ 内的完整仿真状态和动作序列。我们常用的度量指标包括:
-
到目标的距离
:从最终位姿到地图中的目标路径点的距离
-
车道选择偏差
:距离最右侧车道越远的车道,其递增成本越高,
-
最大偏航率
:仿真轨迹期间记录的最大偏航率,以及
-
简单策略成本
:用于打破平局的给定策略的硬编码常量成本。
这些指标用于衡量目标达成、安全性、“软性”驾驶规则的执行以及乘坐舒适性。组合这些指标的难点在于,每个指标返回的成本具有不同单位和不同的预期成本分布。我们通过对每个指标的归一化分数进行线性组合,计算每项策略得分,从而将这些成本合并为每项策略的单一评分。对于每个指标 $m_j$,我们计算相应的权重 $w_j$,该权重编码了该指标的经验调优的重要性,根据用户需求以及该指标在给定策略集内的信息性程度。我们降低那些在策略间变化过小的信息性不足指标的权重。
V. 评估

A. 自动驾驶车辆平台
在我们的实车实验中,使用了自动驾驶车辆平台(见图2)。该自动驾驶汽车是一辆配备线控驱动系统的福特融合,搭载四个Velodyne HDL-32E 3D激光雷达扫描仪、一个Applanix POS-LV 420惯性导航系统(INS)、一个前向的Point Grey Flea3相机以及多个其他传感器。车载的五节点计算机集群实时执行系统的全部规划、控制和感知任务。
车辆使用由测量车通过3D激光雷达扫描仪构建的运行区域先验地图。这些先验地图捕捉了环境信息,如激光雷达反射率和道路高度,并用于定位和其他感知任务。道路网络被编码为度量-拓扑地图,使用一种导数路线网络定义文件(RNDF)格式[21],提供有关道路路段及其车道位置和连接信息。
车辆上的动态物体跟踪利用激光雷达测距数据,提供对其他交通参与者状态的估计。静态障碍物的几何形状和位置也通过车载激光雷达测量推断得出。
B. 仿真环境
为了在MPDM中前向仿真策略的后果以及评估我们的系统,我们开发了一个多智能体交通仿真引擎。该引擎能够仿真相关智能体的系统动力学和感知,并通过轻量级通信与编组框架(LCM)[22] 与实车平台的软件架构完全集成。
VI. 结果
我们现在报告MPDM在实车自动驾驶车辆平台和仿真环境中的评估结果。我们首先在一系列超车操作中演示了实车上的MPDM,其中我们的算法决定在首选行驶车道上超越慢速车辆。通过这些真实世界的结果,我们随后通过将模拟器的输出结果与我方车辆及其他交通参与者的真实轨迹进行比较,展示了模拟器的性能。最后,我们在一个模拟的汇流场景中演示了我们的算法。实验中的所有策略选择均使用 $H = 10$ 秒的规划时域,并以 $\Delta t = 0.25$ 秒的时间步长进行离散化。
A. 实车超车场景
我们在封闭测试轨道上的多车道环境中评估了 MPDM,场景为我方车辆超越一辆较慢的人工控制车辆。在这些实验中,我方车辆从右车道开始行驶,随着前进,在其首选行驶车道上遇到一辆限制其前进的慢速车辆。此时,由于所使用的评分函数的作用,车辆决定执行超车操作以超越该慢速车辆。图3展示了在此场景下进行的14次试验中,我方受控车辆的轨迹以及超车操作进行到一半时被超车辆的位置。
本场景中,受控车辆考虑的策略为保持车道、向左变道和向右变道,而被超车辆的未来状态则通过单一的保持车道策略进行模拟。

图4展示了超车操作过程中各策略得分的演变情况。
B. 前向仿真评估
在对上述一系列超车操作运行我们的算法后,我们能够将策略的前向仿真结果与我方车辆及被超车辆的实际真实轨迹进行比较。为此,我们在整个超车操作过程中记录了我方车辆(通过其位姿估计系统)和被超车辆(通过动态物体追踪器)的位置。

图6显示了每种策略的预测误差,即策略的模拟结果与相关车辆实际轨迹之间的均方根(RMS)差异。结果展示了在所有超车操作中,每个时间步的策略选择在整个规划时域前5秒内的平均结果。计算预测时的延迟效应体现在 $t = 0$ s时误差非零。也就是说,假设的世界状态已从仿真中使用的初始状态发生变化。可以观察到受控车辆的仿真策略与其实际轨迹之间存在差异,这表现为仿真动力学模型与车辆速度控制器在纵向轴上的不同。关于被超车辆的预测误差,在执行向右变道策略时尤为不均匀。这是由于动态物体追踪器性能不足所致,因为在完成超车操作时,被超车辆已被远远甩在后面。
尽管存在这些不准确之处,我们的仿真引擎的性能仍足以支持决策过程完成超车操作。
C. 仿真中的合流场景

图5展示了一个模拟合流场景,以突出前向仿真其他车辆策略如何使 MPDM 能够利用其他车辆的反应。为了说明我们多车辆策略模型的表达能力,我们评估了一种即使没有足够间隙也尝试并入车流的策略。通过预测车辆2会减速并与驶入其路径的车辆保持相同速度,该策略的预期结果是可行的,且不会过于保守。传统轨迹优化算法(不考虑其他车辆对我方车辆行为的反应)很可能无法执行此操作,因为它无法预测到足够大的间隙将出现。由于这是仿真,我们为交通中的其他三辆车选择了合适的策略参数,使得这些车辆会避免与路径上的车辆发生碰撞;并且通过使用相同的策略参数,我们能够像在策略选择仿真中一样精确地在车辆1和车辆2之间汇流。请注意,由于所有车辆都执行安全行为,包括为路径上的车辆减速或停车,即使车辆2加速进入我方路径,任何正在运行的策略仍会避免碰撞。作为对比,我们可以关闭对其他车辆预期反应的预测,此时我方车辆将更为保守地等待,直到车辆2和车辆3均通过后才变道进入车道。
D. 性能
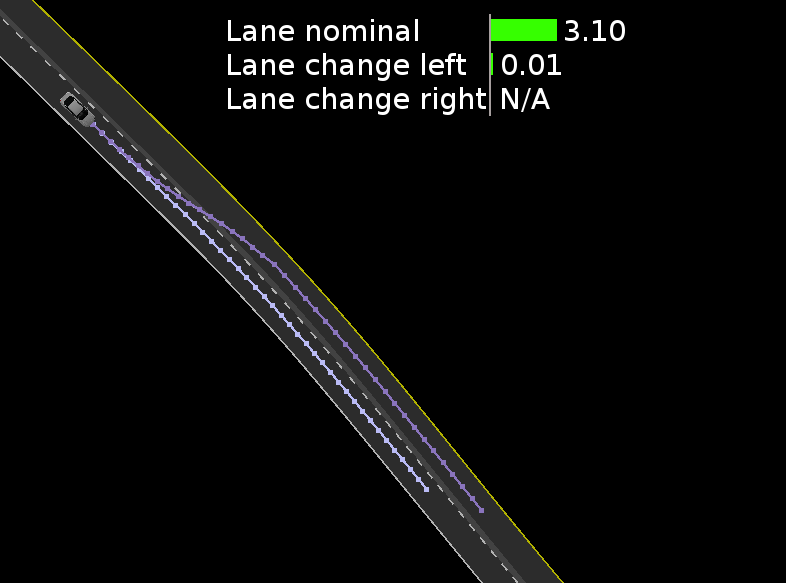
图7展示了在开发用笔记本电脑(2.8GHz Intel i7)上采样策略结果并执行策略选择所需的计算时间,该硬件与车辆上集群节点的硬件相似。为了获得作为采样策略数量函数所需的时间,我们在模拟场景中运行MPDM,并逐步增加策略数量(从1到20)。正如预期,策略选择过程所需的计算时间随着策略数量和规划时域的增加呈线性增长,前提是这些采样策略具有相似的计算需求。
VII. 结论与未来工作
本文提出了一种在包含智能体之间广泛耦合交互的动态环境中进行决策的系统化方法。通过以策略的形式显式建模环境中其他车辆的合理行为,我们能够在更准确地评估自身行为后果的同时,做出有依据的高层行为决策。我们在真实世界环境中的超车场景中验证了该方法的可行性,并进一步证明MPDM能够处理汇流等交通情况,在这些情况下大多数其他方法无法合理考虑车辆之间的交互。
在未来工作中,我们将把行为预测集成到系统中,以系统化方法确定其他车辆最可能遵循的策略,从而实现更复杂的车辆交互。























 3448
3448

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








