军队文职数学1笔试

1.函数极限连续

1.奇偶性和周期性

导数是周期函数并且导数的定积分，才能推出原函数是周期函数

原函数奇导函数偶

原函数偶导函数奇

导函数奇原函数偶

导函数偶推不出来原函数奇

f(t)+f(-t)永远是偶

f(t)-f(-t)永远是奇函数

 

2.复合函数

画图分析或者直接代入

 3.求极限

1.无穷比无穷型的简单做法

2.无穷-无穷型

 凑平方差公式

3.0比0型

sinx=x-x^3/6

arcsinx=x+x3/6

cosx=1-x2/2

tanx=x+x3/3

arctanx=x-x3/3

ln(1+x)=x-x2/2

 4.无穷乘0型

5.分段函数

必须求左右极限

a的1/x次幂，必须求左右极限

6.极限拆分

当两个函数的极限都不是无穷时，才可以拆分

相乘也是同理

7.判断极大值还是极小值

 

8.夹逼定理求极限

 

4.求渐近线 

5.求间断点

2.一元函数微分学

1.判断导数是否存在

2.函数不可导点

可能不可导：分段函数分段处，分母为0

然后一一验证

3.求导

1.定义求导

2.幂函数求导

遇到幂函数直接变成e的多少次方的形式 

3.隐函数求导

 

4.隐函数求导和极限定义

5.抽象函数，用定义求导

6.参数方程求导

7.求高阶导

1. 简单分式

2.ln

3.麦克劳林公式求高阶导

4.求函数凹凸区间和拐点

5.求切线方程和法线方程

1.直角坐标

2.极坐标

6.图像题

3. 一元函数积分学

1.求简单积分

2.第一类换元法

1.分式三角函数

上下同时除以cosx,凑tanx

直接令u=cosx,   dx=1/u导=-1/sinx du

3.第二类换元法

加谈减塞剩下负x散

4.分部积分法

u的顺序，反对幂三指

5.计算定积分的性质

1.周期函数

2.下标为0时

6.积分中值定理

7.定积分求导

8.定积分求面积

 

9.求体积

4.微分方程

1.线性和非线性的概念

2.可分离变量

3.齐次微分方程 

没有常数的微分方程

4.一阶线性微分方程

5.伯努利方程

不考通解

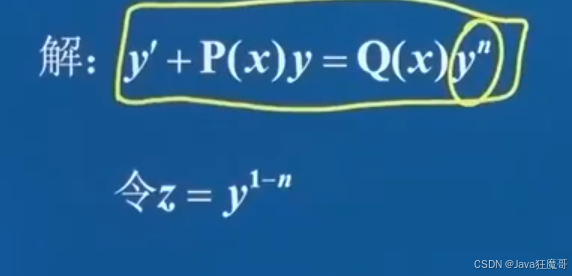
6.全微分方程

7.二阶线性微分方程

1.齐次

2.非齐次

λ是e的多少次幂，λ 不是跟就不乘x，一个跟就乘一个x，两个根就乘x方

8.可降阶高阶微分方程

9. 不用公式求微分方程

5.多元函数微分学

1.抽象函数求偏导

横乘纵加

2.抽象隐函数求偏导

先看看能不能直接求偏导，如果不能再套公式

3.全微分 

4.已知全微分求系数

5.曲线方向向量和法平面

6.切平面

7.切平面和法线

5.方向导数

6.梯度就是向量

  

7.多元函数求极值

8.求最值

6.二重积分

1.三个未知数的二重积分

2.区域对称 

3.极坐标变换

4.直角坐标变换 

5.关于y=x对称

6. 通过积分区域形心计算

7.二重积分中值定理

 8.函数表达式中含有二重积分

9.曲线积分

1.对称性

被积区域关于y轴对称,被积函数是关于x的奇函数，那么曲线积分等于0

2.形心

3.第二类曲线积分

4.格林公式

5.与路径无关

10.曲面积分

1.一投二代三替换

2.对称性

3.轮换对称性

4.曲面积分d的形式

5.高斯公式

闭合曲面 

1.导数

1.求导公式

2.隐函数求导

 

3.参数方程求导

 4.求极值

y导等于0极值

y导导大于0极小值

y导导小于0极大值

5.凹凸区间与拐点

凸区间：y导导<0的区间

凹区间：y导导>0的区间

驻点：导数等于0

6.导数定义 

 

7.根据导数定义式求导 

分段点的导数必须要用导数定义式

8.取对数求导

9.微分中值定理

1.罗尔定理（端点函数值相等）

函数的导数至少有一点等于0，平行于x轴

2. 拉格朗日中值定理

函数的导数至少有一点平行于AB

 

3.柯西中值定理 

 

4.泰勒中值定理（求极限）

 

2.三角函数公式

      

1.奇偶函数

  a是奇数就是奇函数，a是偶数就是偶函数

 奇函数

奇函数的绝对值是偶函数

f(x)+f(-x)是偶函数，例如

f(x)是奇函数，f(|x|)大概率是奇函数

3.求极限

1.换算公式

1.0比0型换算公式，等价无穷小代换

 2.指数中带有复杂度式子

2.给出f(x)的关系求f(x) 

3.f(x) 在 x=0的时候极限存在，就说明：左极限=右极限=f(0)

如果左右极限不相等说明极限不存在 

4.注意根式有理化，没有分数就凑成分数

5.注意法则可以交换如果式子带有arccos可以换到极限外边

6.数列求极限（夹逼定理）

其实就是放缩 

数列收敛

单调递增有上界数列收敛，单调递减有下界数列收敛 

7.高阶无穷小和低阶无穷小

8.判断函数是否连续

f(x)在0处的极限等于f(0)，如果有左右极限的区别那么，左极限要等于右极限，这样的函数是连续的

9.间断点

第一类间断点：左右极限都存在

极限存在就代表左右极限相等

可去间断点：左极限=右极限  但不等于 函数值

跳跃间断点：左极限 不等于 右极限

 第二类间断点：左右极限不存在（分母无穷大）

做题方法 

 10.渐近线

铅直渐近线：导数等于无穷

水平渐近线：导数等于0

斜渐近线：

 

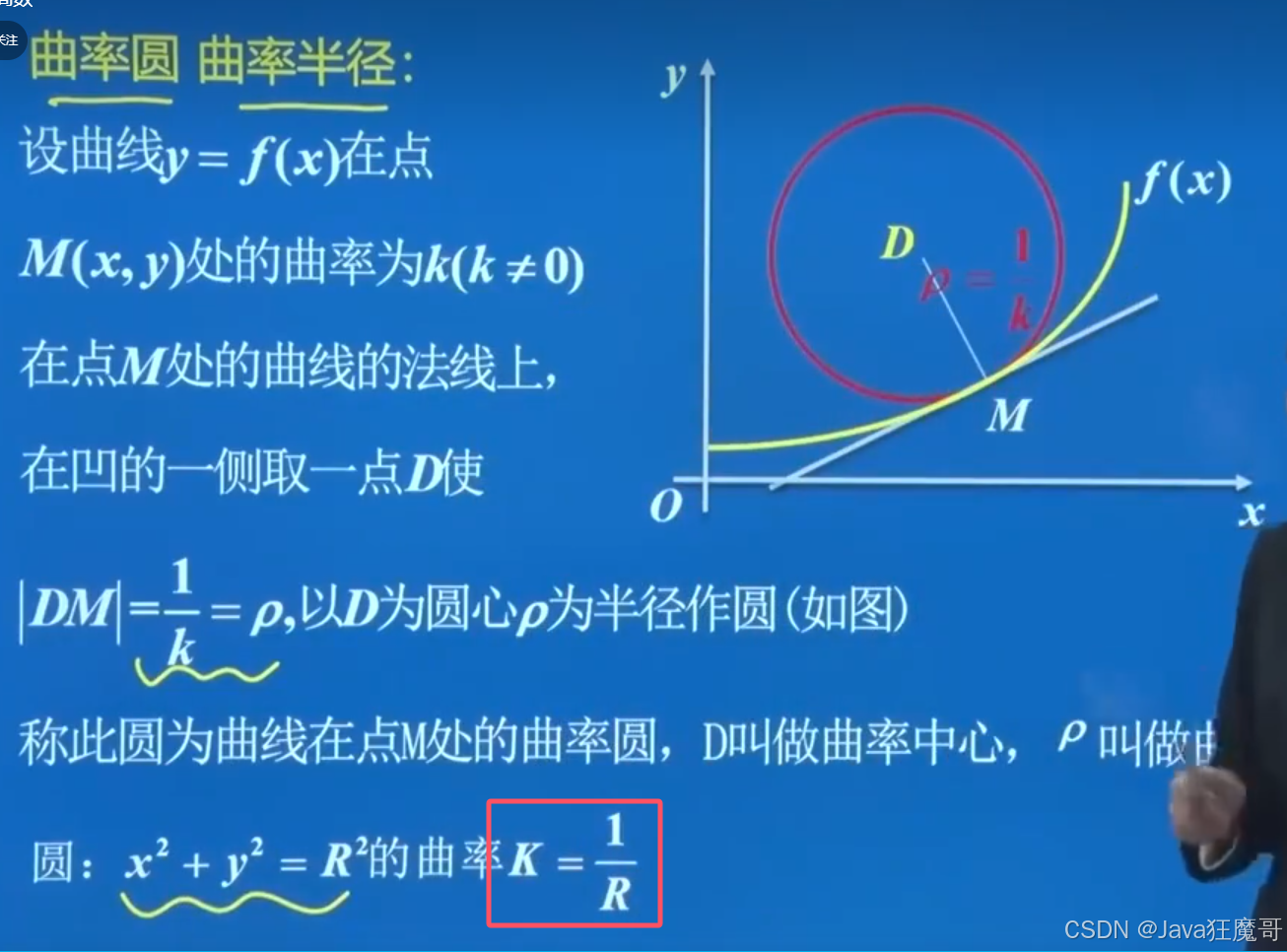
11.曲率

 

曲率圆

 

参数方程：x导y导导-x导导y导/x导方+y导方整体的二分之三次幂

4.积分

1. 不定积分

1.求不定积分的公式

 

 

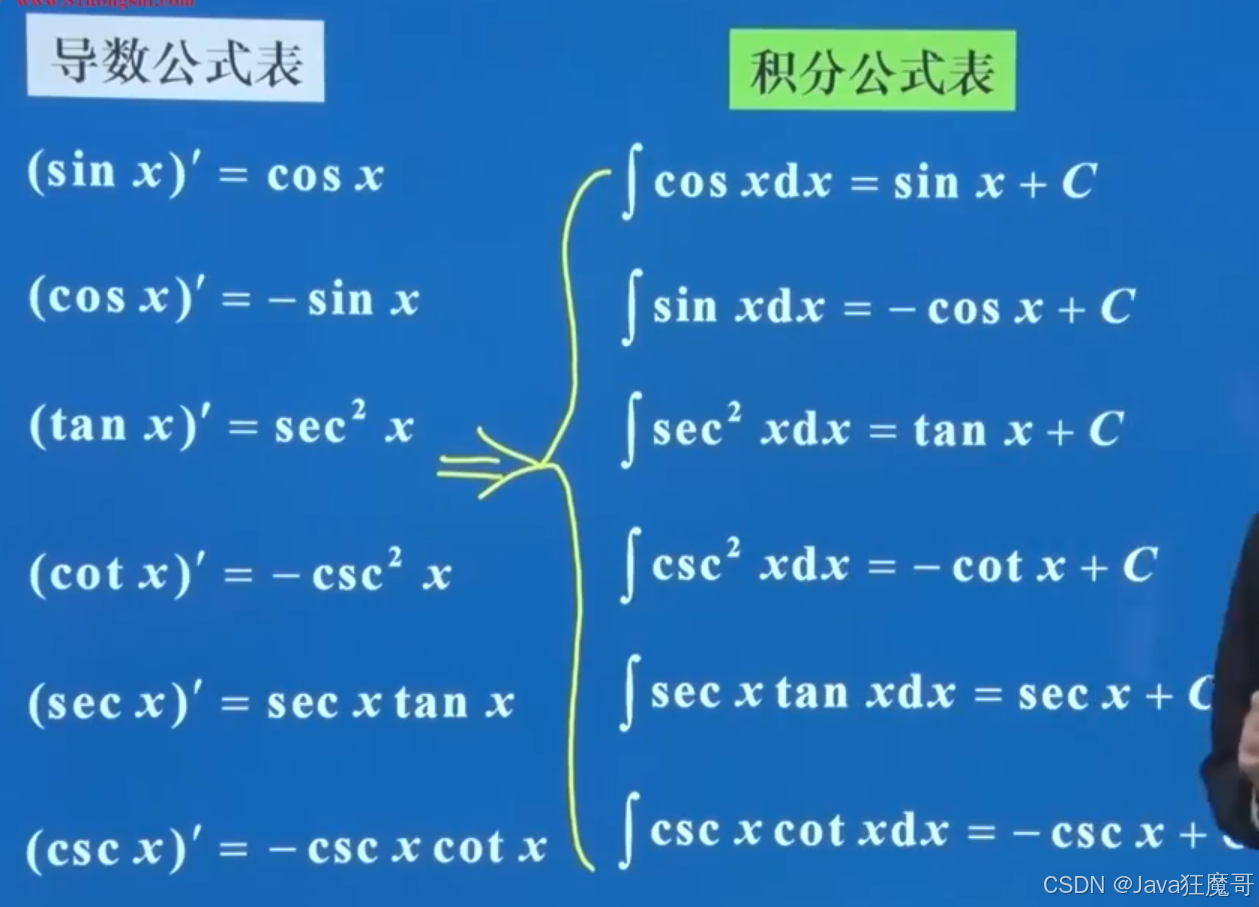
2. 第一类换元法

a是b的原函数，就说明b的积分等于a，就说明 

3.第二类换元积分法

1.根式换元（根号里x是一次的）

2. 三角换元（根号里x是2次的） 正tan负塞，-x就是散

 正tan负塞，-x就是散

3.分部积分

 u的顺序，反对幂三指

 4.有理分式积分

2.定积分

1.定积分是一个常数，同时对两边积分

 

2.积分上限函数

 

3.积分中值定理

注意分离x和t，x是常数

 

4.定积分换元法

 

换元不一定换限 

5.定积分的分步积分法

6.反常积分（界限为无穷） 

 

7.以角度为积分的变量

8.弧长 

1.参数方程形式

2.正常形式

 

3.星形线弧长

 9.体积

1.绕x轴旋转

y=x

2.绕y轴旋转

x=y

3.向量

 1.向量单位化

2.向量的投影 

a在b上的投影等于

投影的大小和投影

1.方向角

三角形面积：

2.数量积

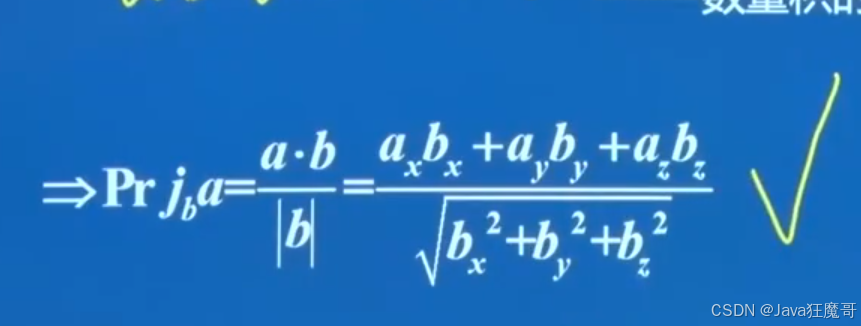
3.点乘

 4.向量叉乘

|a x b|=|a||b|sin

a·b=|a||b|cos

叉乘后的向量垂直与原来两个向量所在的平面

两个向量点乘等于0就说明他俩垂直

两个向量平行就说明叉乘等于0

5.向量平行

3.面

1.旋转曲面

 绕哪个轴旋转哪个变量就不动，剩下的那个变量换成根号下，另外两个变量的正负根号下平方相加

2.柱面

母线平行于哪个轴就 消去哪个给的方程的母线

这个就消去z

3.平面 

1.求过三点的平面方程

2. 判断面与面，面与向量的关系

 3.已知一个面过一点和法向量，求面

4.点到面的距离 

5.两个平面的夹角

6.平面束方程

 

4.直线 

1.判断直线和平面的关系

 2.已知一个点和方向向量

3.点到线的距离

4.切线方程与法平面方程

1.参数方程的切线方程和法平面方程

2. 一般式求切线方程和法平面方程

 3.求曲线在某点的切平面和法线

5.求直线和平面的交点

6.直线和平面的夹角 

4.多元函数微分学

1.求偏导

对谁求导，另外一个就是常数

1.复杂抽象函数情况求偏导 

2.多元隐函数求偏导   

2.二阶混合偏导

先求x还是先求y都一样

3.全微分 

4.多元函数、可导、可微的关系

 一元函数可导必连续

5. 方向导数

沿梯度方向的方向导数最大，方向导数最大值是梯度的模

梯度的方向增加最快，梯度的反方向减少最快

6.梯度

7.极值点，极大值，极小值

驻点不一定是极值点

 8.拉格朗日函数，求最大值

5.二重积分 

1.二重积分的对称性

D关于x轴对称，找关于y的奇偶性

D关于y轴对称，找关于x的奇偶性

如果f（x）既是关于x的奇函数，又是关于y的奇函数，大概率等于0

 2.交换积分次序

3.求积分

先看被积函数

如果x为自变量好求就是先x后y，y为定值， x为函数值

1.公式求二重积分

2.极坐标求积分

只能先dr然后再dQ 

后面的r不能丢

1.极坐标转直角坐标

 

4.求曲面面积

5.二重积分中值定理求极限

 

6.三重积分

1.对称原则

如果是关于x的奇函数，被积区域又是关于yoz面对称，那么这个三重积分等于0 

 2.求三重积分

先化体积，找出xyz的界限

然后，x的界限全是数，y的界限是关于x的表达式，z的界限是关于xy的表达式

3.通过面积求积分

 面积是z的表达式

 4.极坐标的三重积分

7.对称性 

1.二重积分

1.区域关于x轴对称，且被积函数是关于y的奇函数f(-y)=-f(y)，函数没有y积分直接=0

那么积分就等于0

区域关于x轴对称，且被积函数是关于y的偶函数

2.如果区域关于y轴对称，且被积函数是关于x的奇函数

那么积分等于0

8.  通过积分区域的形心计算

1.积分区域是个圆，或者正方形。被积函数是ax+by的形式

那么积分=（a·圆心x+b·圆心y）·面积

2.当被积函数只有ay时，并且积分区域关于y=一个数对称

y是对称轴

积分=ay*D

3.当被积函数只有ax时，并且积分区域关于x=一个数对称

x是对称轴

积分=ax*D

9.比较二重积分大小

相同区域时，函数值越大积分越大

相同函数时，区域是一个包含另一个，那么区域大的大，前提是区域大于0

10.函数值中带有二重积分

 

11.曲线积分

1.对弧长的积分

 界限是大的在上，角度也是

 2.对坐标的积分

3.格林公式

 

 

 凑格林公式

 4.全微分

Q对x的偏导=P对y的偏导

 

12.曲面积分 

1.一投，二换，三定限

2.高斯公式 

曲面必须封闭 ，高斯公式是偏导相加

3.斯托克斯公式

13.级数 

1.判断级数敛散性 

  1.利用定义判断

数列有界是数列收敛的充要条件

2.利用大小判定

 3.求极限

求数列在n趋于无穷的极限，结果=0就是收敛

4.比值判断

5.交错级数

函数单调递减，并且极限=0

 2.绝对收敛和条件收敛

3.收敛半径

 

4.收敛区间，阿贝尔定理

 

 5.收敛域

只讨论端点 

 6.和函数

把级数求和

等比数列前n项和公式

7.f(x)展成幂级数

 8.傅里叶级数

1.傅里叶系数

 2.傅里叶级数展开

3.狄利克雷收敛定理

如果没有间断点，函数收敛于当前值。如果有间断点，求下左右极限的和再除以2

 12.微分方程

1.微分方程的阶和线性

y导数最高阶数

y以及y的导数都是1次

2.通解和特解

3.求通解

1.一阶线性微分方程

把y和x都整理到一边，然后求积分

2.非线性微分方程 ，伯努利方程

3.判断常微分方程是否是全微分方程

偏导数相等就是不相等就不是

 4.二阶常系数齐次线性微分方程

 可能△<0

 5.二阶常系数非齐次线性微分方程

没有解就不乘x，有一个就乘x，有两个重根就乘x方 

6.可降阶的高阶微分方程

7.高阶线性微分方程

1.微分方程解的结构