TF-Lite：Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference

摘要

智能移动设备日益增长的普及度和基于深度学习模型令人畏惧的计算成本需要高效且精确的终端推理方案。我们提出了一个量化方案，它允许仅使用整数运算来执行推断方案，在通用的整数运算硬件上执行地要比浮点推断高效很多。我们也协同设计了一种训练过程来保存量化后的模型精度，结果是提出的量化方案在精度和设备延迟上取得了一个很好的平衡，即使在MobileNets（一种精简网络family，以实时效率而著名）上取得了很大的提高，同时在ImageNet分类任务和COCO检测任务上效果都很好。

1. Introduction

由于要在移动端部署深度学习模型，这产生了一个蓬勃发展的研究领域——在精度几乎无损的前提下，减少模型的尺寸和推理延迟。在这个领域的研究主要分为两个部分：（1）第一类，以MobileNet、ShuffleNet、SqueezeNet为例，设计新颖的网络开发计算和内存资源高效的操作；（2）第二个类别就是直接将CNN模型的权重和激活值从32位浮点量化为低bit的参数，这方面的工作有三值化、二值化、XNORNet，这同时也是我们的研究重点。尽管它们的想法很好，现在的量化方法缺乏对精度和延迟之间的平衡。

许多量化方法没有在真实的硬件上验证性能的提高，同时，只对权重做量化通常仅可以减少设备内存需求，对计算效率影响不大。值得注意的是二值化和三值化网络，它们可以用移位操作和bitcount操作来代替原来的乘加操作。然而，移位操作通常只在定制硬件上很高效，而在乘加优化的已经存在的平台上，而在这种平台上，正确的使用流水线后乘加运算成本不见得比单独的加法高。而且，如果操作数位数很宽，乘法就很昂贵，由此我们需要降低参数的精度。

这本篇论文中，我们在通用的移动硬件上（不需要特定的加速），有效地在精度和延迟之间获得平衡，我们的特殊贡献为：

• 我们提出了一种量化方案（见于2.1节），将权重和激活值都量化为8-bit整数，只有一小部分参数（bias）仍然是32-bit 整数；
• 我们提出了一种量化推理框架，可以在诸如Qualcomm Hexagon这样的只做整数运算的硬件上高效实现（见于2.2、2.3节），同时我们描述了在ARM NEON（附录B）上一个高效且精确的实现；
• 我们提出了一种量化训练方案（见于section 3），它可以和我们的量化推理协同设计共同减小精度上的损失；
• 我们将我们的框架应用到基于MobileNets的高效分类和检测系统中，在流行的ARM CPUs（section 4）中给出了基准测试结果，展示了延迟-精度上取得了最好的平衡（包括ImageNet分类和COCO目标检测数据集上）。

2. 量化推理

2.1 量化方案

我们的量化方案是在推理期间只做整数算术运算，在训练期间做浮点运算。具体来讲，量化方案就是整数 $q$ 到实数 $r$ 的仿射映射：

其中$S$和$Z$都是常数，对每一层的$Array$使用一对$S/Z$参数，即分层量化，层内共用一组$S/Z$参数，不同层参数不同。

通常权重和激活值要进行8-bit量化，而bias要做32-bit量化；对于8-bit量化，$q和Z$为8位整数，$S$为缩放因子，是实数，$r$是未量化之前的值，也是实数。

那么我们怎么将实数$Aaary$量化为整数$Array$呢？对于矩阵中的每一个实数，怎样获得其对应的整数$q$，以及一组参数$S/Z$？接下来我们先来解释一下S和Z的具体含义。

常数S是缩放因子。常数Z是偏移shift，代表"Zero-Point"，就是为了让实数r的最小值min和量化数q的下限0对应，和q是同类型的数。

各参数类型定义如下：

template<typename QType>                    // e.q.  QType=uint8
struch QuantizedBuffer{
	vector<QType> q;                        // the quantized values
	float S;                                // the scale
	QType Z;                                // the zero-point
}

2.2 仅做整数算术运算的矩阵乘法

现在我们来展示如何对输入和权重做矩阵乘法，考虑两个$N\times N$的实数方阵$r_1和r_2$，它们之间的点积可以表示为$r_3=r_1{r}_2$，我们用$r_{\alpha }(\alpha =1,2,3)$来表示三个矩阵，其中$r_{\alpha }^{(i,j)}，1⩽i,j⩽N$，量化参数为$(S_{\alpha },Z_{\alpha })$。量化后的对应值为$q_{\alpha }^{(i,j)}$：

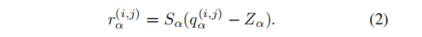
从矩阵乘法的定义，我们有：

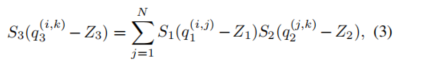
进一步可以写成：

其中M的定义为：

在等式（4）中，唯一的非整数就是乘子$M$，且M仅依赖于量化的缩放因子$S_1,S_2,S_3$，可以离线计算。动脑子的人在这里就会有疑问，这里的$S_3$是激活值的缩放因子，而矩阵乘法还没做，哪里来的$S_3$？答案是激活值的缩放因子$S$是基于大量数据的指数移动平均值统计得到的，在训练完成后，我们对于每层的激活值就会有一个缩放因子。同理$Z_3$也是这样得到的。

我们经验发现M的值总是在区间(0,1)中，因此可以用正则化的形式表示它：

其中$M_0$在区间$[0.5,1)$中，$n$是一个非负整数。归一化因子$M_0$很适合被表达成定点乘数（int16或者int32取决于硬件容量）。举个例子，当使用int32时，表达$M_0$的整数是最接近$2^{31}{M}_0$的int32值。因此乘以$M_0$可以通过定点乘法来实现，同时乘上$2^{-n}$可以通过高效的移位操作来实现。

2.3 zero-points的高效处理

为了高效地执行等式（4），而不需要去做$2N^3$次减法，同时不需要将乘法的操作数扩展到16位，我们将等式（4）变形，得到：

每一个$a_2^{(k)}和{\overline{a_1}}^{(i)}$仅需要N次加法来计算，因此它们总共需要$2N^2$次加法。等式（7）剩下的成本集中在矩阵乘加中：

总共花费了$2N^3$次算术操作。

2.4 典型融合层的实现

我们继续2.3节中的讨论，现在修正等式（7）中的量化矩阵乘法，将“加偏置”和过激活层直接融合进去。

现在我们用$q_1$矩阵表示权重，$q_2$矩阵表示激活值。权重和激活值都是uint8类型的。uint8类型的乘积运算需要一个32-bit的累加器做缓存，我们选择有符号累加器的原因就是偏置也是int32类型的。（9）式中的求和可以用下面的形式表示：

那么偏置是如何量化为int32类型的呢？它的缩放因子和累加器保持一致，为权重和输入激活缩放因子的乘积，zero-points为0：

尽管bias向量被量化为32-bit，但是它们仅占了神经网络一小部分的参数。而且，高精度的使用也满足了需求——由于偏置是直接被加到乘加结果上的，应该尽量减小量化误差。

现在的输出结果是int32类型的，所以仍然有三件事要做：

1. 缩放到由8-bit输出激活的最终尺度，对应的操作是等式（7）中乘上因子M，具体的来讲，它是定点乘法后加移位操作；
2. 之后，再将int32位的数限幅到 [0,255]，然后转换为 uint8 类型；
3. 将uint8类型的值送入激活函数中，这里的激活函数通常是具有钳位功能的ReLU或者ReLU6。

推理过程中量化卷积计算过程

1. 输入 量化的特征图 lhs_quantized_val, uint8类型, 偏移量 lhs_zero_point, int32类型;
2. 输入 量化的卷积核 rhs_quantized_val, uint8类型, 偏移量 rhs_zero_point, int32类型;
3. 转换 unit8 到 int32类型;
4. 每一块卷积求和(int32乘法求和有溢出风险，可换成固定点小数树乘法);
   int32_accumulator += (lhs_quantized_val(i, j) - lhs_zero_point) * (rhs_quantized_val(j, k) - rhs_zero_point);
5. 输入 量化的乘子 quantized_multiplier, int32类型 和 右移次数记录 right_shift, int类型;
6. 计算乘法，得到int32类型的结果 (int32乘法有溢出风险，可换成固定点小数树乘法);
   quantized_multiplier * int32_accumulator
   
7. 再左移动 right_shift 位还原，得到 int32的结果;
8. 最后再加上 结果的偏移量 result_zero_point;
   (7和8的顺序和 官方说的先后顺序颠倒);
9. 将int32类型结果 限幅到[0, 255], 再强制转换到 uint8类型;
10. 之后再 反量化到浮点数，更新统计输出值分布信息 max, min;
11. 再量化回 uint8;
11. 之后 经过 量化激活层;
12. 最后 反量化到 浮点数，本层网络输出;

13. 进入下一层
    循环执行 1~12 步骤

若有连续的层需要量化操作时，就没必要进行反量化了。。比如上面步骤的 10→1110→11，实际上是可以省略的【但相应的。。可能会带来乘法加法累积造成的溢出】

3. 模拟量化训练

通常训练量化网络的方法是以浮点数训练，然后量化结果权重（有时再辅助以额外的量化后训练作为微调）。我们发现这种方法对于大模型效果不错，但是在小模型上有明显的精度下降。导致这种情况的原因有两点：

1. 不同输出通道之间权重范围差异很大（而Section 2中对于同一层的所有通道的参数的缩放因子和zero-point都是一样的，这使得参数分布在较小范围的通道会有较高的相对错误）；
2. 离群权重值，使所有剩下的权重量化都不太精确；

本文提出在前向的时候进行模拟量化的方法。后向传播不变，仍按照浮点型存储数据。在前向传播时，在推断时需要量化的地方，插入伪量化操作。这里需要注意的是，

（1）权重是在与输入进行卷积前进行量化，如果有BN层，需要将BN层的参数在量化前folded into权重中。
（2）activation的量化在激活函数或者bypass（resnet）之后进行。

伪量化操作为：

即先量化，再反量化。

3.1 量化范围学习

对于权重和激活值量化，它们的量化范围是不同的：

• 对于权重，基本的思想是取 $a:=minw,b:=maxw$。我们对权重做一个微调的调整，一旦被量化为 int8类型的值，不会取到-128，范围在[-127, 127]（从[0, 255]减去128得到范围[-128, 127]，再做微调），这样做有什么好处吗？就永远不会出现 -128*-128这种情况，所以点积的结果的绝对值不会超过$2^{14}$，那么累加器可能就只需要16位了，不需要32位的累加器（具体可见附录B）；
• 对于激活值，范围取决于网络的输入。在训练时，用指数移动平均来收集activation的range [a,b]，平滑参数接近1.【若范围快速变化时，指数移动平均会延迟反映出来，所以在训练初期（5万步到200万步）时，不量化activation是有用的】；

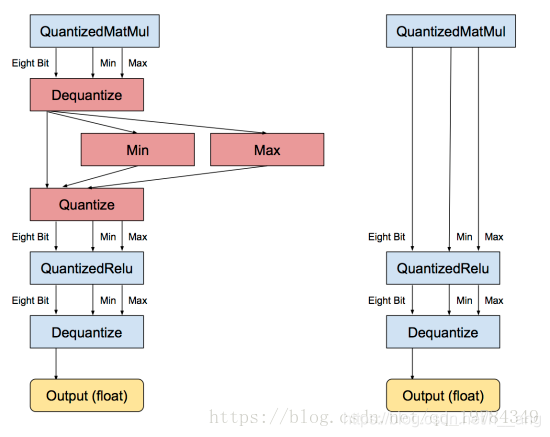
在Tensorflow中，量化的算法描述如下：

Figure 1.1a和b分别展示了对于一个简单的卷积层在量化前后的Tensorflow计算图

关于跳层加法和拼接这样的结构应该如何处理呢？

1. 对于跳层加法，要做加法操作的两层feature map需要具有相同的缩放因子，所以一层的输入需要使用定点乘子 $M=S_1/S_2$被缩放到和另一层输入相同的缩放因子，最后，结果需要被缩放到适合输出阵列的缩放程度（即要先反量化再量化）；
2. 对于跳层拼接，为了使得这个过程无损，我们引入了一个要求：在同一个拼接层的输入和输出激活值具有相同的量化参数，这样在拼接时就没有问题了；

3.2 折叠BN层

可以将BN层的参数折叠到前面的卷积或者全连接层，从而得到一个没有BN层的网络结构：

同理，可以求得$b_{fold}$。

4. 实验结果

4.1 对大网络的量化训练

4.2 量化MobileNets

参考文献

https://blog.csdn.net/qq_19784349/article/details/82883271
https://www.tensorflow.org/lite/performance/quantization_spec