背景知识
光流(optical flow)是空间运动物体在观察成像平面上的像素运动的瞬时速度。
光流法是利用图像序列中像素在时间域上的变化以及相邻帧之间的相关性来找到上一帧跟当前帧之间存在的对应关系,从而计算出相邻帧之间物体的运动信息的一种方法。
通常将二维图像平面特定坐标点上的灰度瞬时变化率定义为光流矢量。
光流的物理意义
一般而言,光流是由于场景中前景目标本身的移动、相机的运动,或者两者的共同运动所产生的。
当人的眼睛观察运动物体时,物体的景象在人眼的视网膜上形成一系列连续变化的图像,这一系列连续变化的信息不断“流过”视网膜(即图像平面),好像一种光的“流”,故称之为光流。光流表达了图像的变化,由于它包含了目标运动的信息,因此可被观察者用来确定目标的运动情况。
图(1)展示的便是三维空间内物体的运动在二维成像平面上的投影。得到的是一个描述位置变化的二维矢量,但在运动间隔极小的情况下,我们通常将其视为一个描述该点瞬时速度的二维矢量 u = ( u , v ) u=(u,v) u=(u,v) ,称为光流矢量。
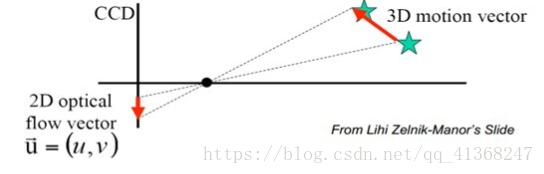
图1 三维运动在二维平面内的投影
在不引入额外约束的情况下,无法在图像中的一点上独立于相邻点计算光流,因为每个图像点的速度场具有两个分量,而图像平面中某个点由于运动而产生的图像亮度变化仅产生一个约束。
光流场
在空间中,运动可以用运动场描述,而在一个图像平面上,物体的运动往往是通过图像序列中不同图像灰度分布的不同体现的,从而,空间中的运动场转移到图像上就表示为光流场(optical flow field)。
光流场是一个二维矢量场,它反映了图像上每一点灰度的变化趋势,可看成是带有灰度的像素点在图像平面上运动而产生的瞬时速度场。它包含的信息即是各像点的瞬时运动速度矢量信息。
研究光流场的目的就是为了从序列图像中近似计算不能直接得到的运动场。光流场在理想情况下,光流场对应于运动场。
光流法基本原理
基本假设条件
-
亮度恒定不变。即同一目标在不同帧间运动时,其亮度不会发生改变。这是基本光流法的假定(所有光流法变种都必须满足),用于得到光流法基本方程;
-
时间连续或运动是“小运动”。即时间的变化不会引起目标位置的剧烈变化,相邻帧之间位移要比较小。同样也是光流法不可或缺的假定。
基本约束方程
考虑一个像素
I
(
x
,
y
,
t
)
I(x,y,t)
I(x,y,t) 在第一帧的光强度(其中
t
t
t 代表其所在的时间维度)。它移动了
(
d
x
,
d
y
)
(dx,dy)
(dx,dy) 的距离到下一帧,用了
d
t
dt
dt 时间。因为是同一个像素点,依据上文提到的第一个假设我们认为该像素在运动前后的光强度是不变的,即:
I
(
x
,
y
,
t
)
=
I
(
x
+
d
x
,
y
+
d
y
,
t
+
d
t
)
I(x, y, t)=\mathrm{I}(\mathrm{x}+\mathrm{dx}, \mathrm{y}+\mathrm{dy}, \mathrm{t}+\mathrm{dt})
I(x,y,t)=I(x+dx,y+dy,t+dt)
将(1)式右端进行泰勒展开,得
I
(
x
,
y
,
t
)
=
I
(
c
,
y
,
t
)
+
∂
I
∂
x
d
x
+
∂
I
∂
y
d
y
+
∂
I
∂
t
d
t
+
ε
I(x, y, t)=\mathrm{I}(c, \mathrm{y}, \mathrm{t})+\frac{\partial I}{\partial x} d x+\frac{\partial I}{\partial y} d y+\frac{\partial I}{\partial t} d t+\varepsilon
I(x,y,t)=I(c,y,t)+∂x∂Idx+∂y∂Idy+∂t∂Idt+ε
其中
ε
ε
ε 代表二阶无穷小项,可忽略不计。再将(2)代人(1)后同除
d
t
dt
dt ,可得:
∂
I
∂
x
d
x
d
t
+
∂
I
∂
y
d
y
d
t
+
∂
I
∂
t
d
t
d
t
=
0
\frac{\partial I}{\partial x} \frac{d x}{d t}+\frac{\partial I}{\partial y} \frac{d y}{d t}+\frac{\partial I}{\partial t} \frac{d t}{d t}=0
∂x∂Idtdx+∂y∂Idtdy+∂t∂Idtdt=0
设
u
,
v
u,v
u,v 分别为沿X轴与Y轴的速度矢量,得:
u
=
d
x
d
t
,
v
=
d
y
d
t
\mathrm{u}=\frac{d x}{d t}, v=\frac{d y}{d t}
u=dtdx,v=dtdy
令
I
x
=
∂
I
∂
x
,
I
y
=
∂
I
∂
y
,
I
t
=
∂
I
∂
t
I_{x}=\frac{\partial I}{\partial x}, I_{y}=\frac{\partial I}{\partial y}, I_{t}=\frac{\partial I}{\partial t}
Ix=∂x∂I,Iy=∂y∂I,It=∂t∂I 分别表示图像中像素点的灰度沿
X
,
Y
,
T
\mathrm{X},\mathrm{Y},\mathrm{T}
X,Y,T 方向的偏导数。综上,式(3)可以写为:
I
x
u
+
I
y
v
+
I
t
=
0
I_{x} u+I_{y} v+I_{t}=0
Ixu+Iyv+It=0
其中,
I
x
,
I
y
,
I
t
I_{x},I_{y},I_{t}
Ix,Iy,It 均可由图像数据求得,而
(
u
,
v
)
(u,v)
(u,v) 即为所求光流矢量。
约束方程只有一个,而方程的未知量有两个,这种情况下无法求得u和v的确切值。此时需要引入另外的约束条件,从不同的角度引入约束条件,导致了不同光流场计算方法。按照理论基础与数学方法的区别把它们分成四种:基于梯度(微分)的方法、基于匹配的方法、基于能量(频率)的方法、基于相位的方法和神经动力学方法。
基于梯度的方法
基于梯度的方法又称为微分法,它是利用时变图像灰度(或其滤波形式)的时空微分(即时空梯度函数)来计算像素的速度矢量。
由于计算简单和较好的结果,该方法得到了广泛应用和研究。典型的代表是Horn-Schunck算法与Lucas-Kanade(LK)算法。
Horn-Schunck算法在光流基本约束方程的基础上附加了全局平滑假设,假设在整个图像上光流的变化是光滑的,即物体运动矢量是平滑的或只是缓慢变化的。
基于此思想,大量的改进算法不断提出。Nagel采用有条件的平滑约束,即通过加权矩阵的控制对梯度进行不同平滑处理;Black和Anandan针对多运动的估计问题,提出了分段平滑的方法。
基于匹配的方法
基于匹配的光流计算方法包括基于特征和区域的两种。
基于特征的方法不断地对目标主要特征进行定位和跟踪,对目标大的运动和亮度变化具有鲁棒性。存在的问题是光流通常很稀疏,而且特征提取和精确匹配也十分困难。
基于区域的方法先对类似的区域进行定位,然后通过相似区域的位移计算光流。这种方法在视频编码中得到了广泛的应用。然而,它计算的光流仍不稠密。另外,这两种方法估计亚像素精度的光流也有困难,计算量很大。
稠密光流与稀疏光流
可以根据所形成的光流场中二维矢量的疏密程度将光流法分为稠密光流与稀疏光流两种。
稠密光流
稠密光流是一种针对图像或指定的某一片区域进行逐点匹配的图像配准方法,它计算图像上所有的点的偏移量,从而形成一个稠密的光流场。通过这个稠密的光流场,可以进行像素级别的图像配准。
Horn-Schunck算法以及基于区域匹配的大多数光流法都属于稠密光流的范畴。
由于光流矢量稠密,所以其配准后的效果也明显优于稀疏光流配准的效果。但是其副作用也是明显的,由于要计算每个点的偏移量,其计算量也明显较大,时效性较差。
稀疏光流
稀疏光流并不对图像的每个像素点进行逐点计算。它通常需要指定一组点进行跟踪,这组点最好具有某种明显的特性,例如Harris角点等,那么跟踪就会相对稳定和可靠。稀疏跟踪的计算开销比稠密跟踪小得多。
上文提到的基于特征的匹配方法是典型的属于稀疏光流的算法
Horn-Schunck算法论文摘要:
Optical flow cannot be computed locally, since only one independent measurement is available from the image sequence at a point, while the flow velocity has two components. A second constraint is needed. A method for finding the optical flow pattern is presented which assumes that the apparent velocity of the brightness pattern varies smoothly almost everywhere in the image. An iterative implementation is shown which successfully computes the optical flow for a number of synthetic image sequences. The algorithm is robust in that it can handle image sequences that are quantized rather coarsely(粗糙) in space and time. It is also insensitive to quantization of brightness levels and additive noise. Examples are included where the assumption of smoothness is violated at singular points or along lines in the image.
为了解决单点求光流时缺少约束的问题,他们提出一种求光流的方法。首先假定图像每个像素点的速度都变化平滑(全局平滑假设,即物体运动矢量是平滑的或只是缓慢变化的。),然后利用一种迭代的方法求出了许多合成图像序列的光流。这个算法具有很好的鲁棒性(robust)。
公式推导
图案中特定点的亮度是恒定的,因此
d
I
d
t
=
0
\frac{\mathrm{d} I}{\mathrm{d} t}=0
dtdI=0
由式(5)表示的局部流速约束如图2所示。
图2
用另一种方式写式(5),
(
I
x
,
I
y
)
⋅
(
u
,
v
)
=
−
I
t
\left(I_{x}, I_{y}\right) \cdot(u, v)=-I_{t}
(Ix,Iy)⋅(u,v)=−It
因此,沿亮度梯度
(
I
x
,
I
y
)
(I_{x},I_{y})
(Ix,Iy) 方向的运动分量等于
−
I
t
I
x
2
+
I
y
2
-\frac{I_{t}}{\sqrt{I_{x}^{2}+I_{y}^{2}}}
−Ix2+Iy2It
…这里省略一些证明…有空再补…
表达附加约束的一种方法是最小化光速梯度的大小的平方:
(
∂
u
∂
x
)
2
+
(
∂
u
∂
y
)
2
and
(
∂
v
∂
x
)
2
+
(
∂
v
∂
y
)
2
\left(\frac{\partial u}{\partial x}\right)^{2}+\left(\frac{\partial u}{\partial y}\right)^{2} \quad \text { and } \quad\left(\frac{\partial v}{\partial x}\right)^{2}+\left(\frac{\partial v}{\partial y}\right)^{2}
(∂x∂u)2+(∂y∂u)2 and (∂x∂v)2+(∂y∂v)2
光流场平滑度的另一种度量是流的X分量和y分量的拉普拉斯算子的平方和。
∇
2
u
=
∂
2
u
∂
x
2
+
∂
2
u
∂
y
2
and
∇
2
v
=
∂
2
v
∂
x
2
+
∂
2
v
∂
y
2
\nabla^{2} u=\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}} \quad \text { and } \quad \nabla^{2} v=\frac{\partial^{2} v}{\partial x^{2}}+\frac{\partial^{2} v}{\partial y^{2}}
∇2u=∂x2∂2u+∂y2∂2u and ∇2v=∂x2∂2v+∂y2∂2v
光流计算的概念是最小化流中的畸变并获得更好的平滑度。 流量被公式化为一个全局能量函数,该函数将被最小化。 二维图像流的功能为
E
u
,
v
=
∬
[
(
I
x
u
+
I
y
v
+
I
t
)
2
+
α
2
(
∇
2
u
+
∇
2
v
)
]
d
x
d
y
E_{u, v}=\iint\left[\left(I_{x} u+I_{y} v+I_{t}\right)^{2}+\alpha^{2}\left(\nabla^{2} u+\nabla^{2} v\right)\right] d x d y
Eu,v=∬[(Ixu+Iyv+It)2+α2(∇2u+∇2v)]dxdy
其中
α
2
\alpha^{2}
α2 缩放全局平滑度项。 使用变化演算,我们获得
I
x
2
u
+
I
x
I
y
v
+
I
x
I
t
−
α
2
∇
u
=
0
,
and
I
y
2
v
+
I
x
I
y
u
+
I
y
I
t
−
α
2
∇
v
=
0
\begin{array}{l}{I_{x}^{2} u+I_{x} I_{y} v+I_{x} I_{t}-\alpha^{2} \nabla u=0, \text { and }} \\ {I_{y}^{2} v+I_{x} I_{y} u+I_{y} I_{t}-\alpha^{2} \nabla v=0}\end{array}
Ix2u+IxIyv+IxIt−α2∇u=0, and Iy2v+IxIyu+IyIt−α2∇v=0
拉普拉斯算子的数值近似为
∇
u
=
u
ˉ
−
u
\nabla u=\bar{u}-u
∇u=uˉ−u ,其中
u
ˉ
\bar{u}
uˉ 是在位置
(
x
,
y
)
(x,y)
(x,y) 处像素周围的邻域中计算出的
u
u
u 的加权平均值。 图像中每个像素
u
u
u 和
v
v
v 的速度由下式给出:
u
k
+
1
=
u
ˉ
k
−
I
x
[
I
x
u
ˉ
k
+
I
y
v
ˉ
k
+
I
t
]
α
2
+
I
x
2
+
I
y
2
,
and
v
k
+
1
=
v
ˉ
k
−
I
y
[
I
x
u
ˉ
k
+
I
y
v
ˉ
k
+
I
t
]
α
2
+
I
x
2
+
I
y
2
\begin{array}{l}{u^{k+1}=\bar{u}^{k}-\frac{I_{x}\left[I_{x} \bar{u}^{k}+I_{y} \bar{v}^{k}+I_{t}\right]}{\alpha^{2}+I_{x}^{2}+I_{y}^{2}}, \text { and }} \\ {v^{k+1}=\bar{v}^{k}-\frac{I_{y}\left[I_{x} \bar{u}^{k}+I_{y} \bar{v}^{k}+I_{t}\right]}{\alpha^{2}+I_{x}^{2}+I_{y}^{2}}}\end{array}
uk+1=uˉk−α2+Ix2+Iy2Ix[Ixuˉk+Iyvˉk+It], and vk+1=vˉk−α2+Ix2+Iy2Iy[Ixuˉk+Iyvˉk+It]
等式(12)和(13)以迭代方案求解,其中上标
k
+
1
k + 1
k+1 表示要计算的下一个迭代,并且
k
k
k 是最后计算的结果。
在这里,我们可以只关心速度的大小而忽略方向。
V
=
u
2
+
v
2
V=\sqrt{u^{2}+v^{2}}
V=u2+v2
LK算法
LK光流法于1981年提出,最初是用于求稠密光流的,由于算法易于应用在输入图像的一组点上,而成为求稀疏光流的一种重要方法。
LK光流法在原先的光流法两个基本假设的基础上,增加了一个“空间一致”的假设,即所有的相邻像素有相似的行动。也即在目标像素周围 m × m m×m m×m 的区域内,每个像素均拥有相同的光流矢量。以此假设解决式(5) 无法求解的问题。
LK光流法约束方程
在一个小邻域内,LK光流法通过对下式的加权平方和最小化来估计光流矢量
∑
(
x
y
∈
Ω
)
W
2
(
x
)
(
I
x
u
+
I
y
v
+
I
t
)
2
\sum_{(\mathrm{xy} \in \Omega)} W^{2}(x)\left(I_{x} u+I_{y} v+I_{t}\right)^{2}
(xy∈Ω)∑W2(x)(Ixu+Iyv+It)2
上式中
W
2
(
x
)
W^{2}(x)
W2(x) 是一个窗口权重函数,该函数使得邻域中心的加权比周围的大。对于
Ω
Ω
Ω 内的 n 个点
X
1
⋯
X
n
X_1⋯X_n
X1⋯Xn ,设
V
=
(
u
,
v
)
T
,
∇
I
(
X
)
=
(
I
x
,
I
y
)
T
V=(u, v)^{T}, \quad \nabla I(X)=\left(I_{x}, I_{y}\right)^{T}
V=(u,v)T,∇I(X)=(Ix,Iy)T
令 A = ( ∇ I ( X 1 ) , … , ∇ I ( X n ) ) T \mathrm{A}=\left(\nabla I\left(X_{1}\right), \ldots, \nabla I\left(X_{n}\right)\right)^{T} A=(∇I(X1),…,∇I(Xn))T ,即 A = [ I x ( X 1 ) I y ( X 1 ) I x ( X 2 ) I x ( X 2 ) ⋮ ⋮ I x ( X n ) I x ( X n ) ] A=\left[\begin{array}{cc}{I_{x}\left(X_{1}\right)} & {I_{y}\left(X_{1}\right)} \\ {I_{x}\left(X_{2}\right)} & {I_{x}\left(X_{2}\right)} \\ {\vdots} & {\vdots} \\ {I_{x}\left(X_{n}\right)} & {I_{x}\left(X_{n}\right)}\end{array}\right] A=⎣⎢⎢⎢⎡Ix(X1)Ix(X2)⋮Ix(Xn)Iy(X1)Ix(X2)⋮Ix(Xn)⎦⎥⎥⎥⎤
令 W = diag ( W ( X 1 ) , … W ( X n ) ) \mathrm{W}=\operatorname{diag}\left(W\left(X_{1}\right), \ldots W\left(X_{n}\right)\right) W=diag(W(X1),…W(Xn)) ,即 W = [ W ( X 1 ) 0 0 0 0 W ( X 2 ) 0 0 ⋮ ⋮ ⋱ ⋮ 0 0 0 W ( X n ) ] W=\left[\begin{array}{cccc}{W\left(X_{1}\right)} & {0} & {0} & {0} \\ {0} & {W\left(X_{2}\right)} & {0} & {0} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {0} & {0} & {0} & {W\left(X_{n}\right)}\end{array}\right] W=⎣⎢⎢⎢⎡W(X1)0⋮00W(X2)⋮000⋱000⋮W(Xn)⎦⎥⎥⎥⎤
令 b = − ( ∂ I ( X 1 ) ∂ t , … , ∂ I ( X n ) ∂ t ) T \mathrm{b}=-\left(\frac{\partial I\left(X_{1}\right)}{\partial t}, \ldots, \frac{\partial I\left(X_{n}\right)}{\partial t}\right)^{T} b=−(∂t∂I(X1),…,∂t∂I(Xn))T ,即 b = [ I t ( X 1 ) I t ( X 2 ) ⋮ I t ( X n ) ] \mathrm{b}=\left[\begin{array}{c}{I_{t}\left(X_{1}\right)} \\ {I_{t}\left(X_{2}\right)} \\ {\vdots} \\ {I_{t}\left(X_{n}\right)}\end{array}\right] b=⎣⎢⎢⎢⎡It(X1)It(X2)⋮It(Xn)⎦⎥⎥⎥⎤
故上面方程的解可由最小二乘法得到:
A
T
W
2
A
V
=
A
T
W
2
b
A^{T} W^{2} A V=A^{T} W^{2} b
ATW2AV=ATW2b
最后得
V
=
(
A
T
W
2
A
)
−
1
A
T
W
2
b
V = (A^{T} W^{2} A)^{-1}A^{T} W^{2} b
V=(ATW2A)−1ATW2b
通过结合几个邻近像素点的信息,LK光流法通常能够消除光流方程里的多义性。而且,与逐点计算的方法相比,LK方法对图像噪声不敏感。
参考资料
[1] 计算机视觉–光流法(optical flow)简介
[2] Horn B K P , Schunck B G . Determining optical flow[J]. Artificial Intelligence, 1981, 17(1-3):185-203.






















 3179
3179











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








