DPLL的介绍
锁相环是根据一个参考周期波形去同步一个周期波形的装置。本质上讲它是一个自动控制系统。就像汽车定速巡航,要维持那个速度一样。我们只需要理解为跟踪参考源频率和相位的装置即可。通过鉴相值去控制数控振荡器(NCO)的输出以便让最终的鉴相值趋于0。
鉴相器:检测参考输入波形于本地产生的波形之间的相位差。其中Kd为鉴相器增益。
f
(
θ
e
)
=
K
d
∗
θ
e
f(θe) = Kd * θe
f(θe)=Kd∗θe

PI环路滤波器:环路滤波器决定Dpll的动态性能,同时滤除噪声。
E
f
[
n
]
=
K
p
∗
E
d
[
n
]
+
K
i
∗
∑
E
d
[
n
]
Ef[n] = Kp * Ed[n] + Ki * ∑Ed[n]
Ef[n]=Kp∗Ed[n]+Ki∗∑Ed[n]
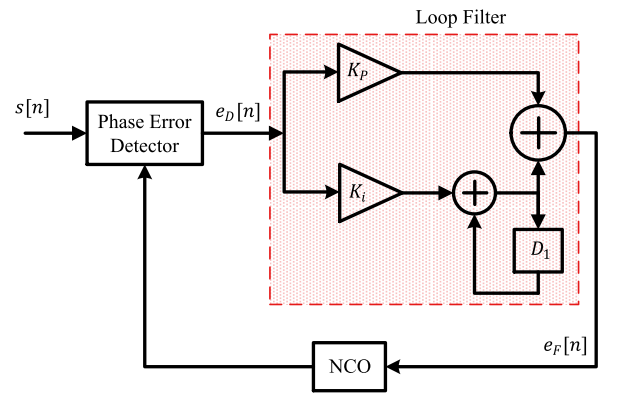
数控振荡器:NCO产生本地离散时间离散值波形,其相位接近输入参考源波形。没次相位调整量的大小由环路滤波器的输出决定。
- 作用1:相位累加,将每个。 O u t p u t = K 0 ∗ ∑ E f [ n ] Output = K0*∑Ef[n] Output=K0∗∑Ef[n] 其中K0代表振荡器增益。
- 作用2:PAC相位幅度转换器。通常使用相位累加器输出字(相位字)作为波形查找表(LUT)的索引,以提供相应的幅度样本。


DPLL的设计
DPLL的响应由阻尼系数(ζ)和固有频率(ωn)决定的。(两者均来自二阶控制系统中的术语)
阻尼系数
PLL相位捕获,表现出振荡行为,该行为可由阻尼因子控制。如将一个篮球扔进地面,有一个重复的阻尼振荡过程,最终平衡。

如上图:单位阶跃响应的输入和输出通过调整阻尼系数得到:
ζ<1时,表现过冲和下冲,为欠阻尼。
ζ>1时,衰减指数的总和,振荡大幅消失,为过阻尼。
ζ=1时,表现在上面两种现象之间,为临界阻尼。
固有频率
后续看到跟踪模式下的DPLL可作为一个低通滤波器,ωn可粗略为环路带宽。
环路带宽:
B
n
=
(
ω
n
/
2
)
(
ζ
+
1
/
4
ζ
)
Bn = (ωn/2)(ζ+1/4ζ)
Bn=(ωn/2)(ζ+1/4ζ)
计算环路常数
软件需要定义Bn 和 ζ
-
环路噪声带宽Bn
小Bn 会滤除大部分噪声。
大Bn 能快速跟踪相位变化。
一般系统Bn值选1%-5%采样率,可满足减少噪声,跟随输入。 -
阻尼系数 ζ
小 ζ,收敛时间快但是会产生阻尼振荡。
大 ζ,不会过冲但是收敛时间会变长。
0.707为经常使用的值,实践时,一般 ζ的范围选择0.5-2。 -
NCO增益K0
在离散时间系统中,NCO增益很容易达到合适的值。 -
鉴相增益Kd
Kd值可以看作固定值的引入。 -
Kp Ki PI滤波器
假设,环路带宽Bn远小于采样率Fs
K
p
=
(
1
/
K
0
K
d
)
(
4
ζ
/
(
ζ
+
1
/
4
ζ
)
)
(
B
n
/
F
s
)
Kp = (1/K0Kd)(4 ζ/ (ζ+1/4 ζ))(Bn/Fs)
Kp=(1/K0Kd)(4ζ/(ζ+1/4ζ))(Bn/Fs)
K
i
=
(
1
/
K
d
K
0
)
(
4
/
(
ζ
+
1
/
4
ζ
)
2
)
(
B
n
/
F
s
)
2
Ki = (1/KdK0)(4/( ζ+1/4 ζ)^2)(Bn/Fs)^2
Ki=(1/KdK0)(4/(ζ+1/4ζ)2)(Bn/Fs)2

import matplotlib.pyplot as plt
import numpy as np
k = 1
N = 15
K_p = 0.19
K_i = 0.0178
K_0 = 1
# 1000个0的集合list
input_signal = np.zeros(1000)
integrator_out = 0
phase_estimate = np.zeros(1000)
e_D = [] # phase-error output
e_F = [] # loop filter output
# 1000个0的集合
sin_out = np.zeros(1000)
# 1000个1的集合
cos_out = np.ones(1000)
# 1000次循环
for n in range(999):
# 设置个输入余弦信号
input_signal[n] = np.cos(2*np.pi*(k/N)*n + np.pi)
# phase detector
try:
e_D.append(input_signal[n] * sin_out[n])
except IndexError:
e_D.append(0)
print(input_signal[n]*sin_out[n])
#loop filter
integrator_out += K_i * e_D[n]
e_F.append(K_p * e_D[n] + integrator_out)
#NCO
try:
phase_estimate[n+1] = phase_estimate[n] + K_0 * e_F[n]
except IndexError:
phase_estimate[n+1] = K_0 * e_F[n]
sin_out[n+1] = -np.sin(2*np.pi*(k/N)*(n+1) + phase_estimate[n])
cos_out[n+1] = np.cos(2*np.pi*(k/N)*(n+1) + phase_estimate[n])
# Create a Figure
fig = plt.figure()
# Set up Axes
ax1 = fig.add_subplot(211)
ax1.plot(cos_out, label='PLL Output')
plt.grid()
ax1.plot(input_signal, label='Input Signal')
plt.legend()
ax1.set_title('Waveforms')
# Show the plot
# plt.show()
ax2 = fig.add_subplot(212)
ax2.plot(e_F)
plt.grid()
ax2.set_title('Filtered Error')
plt.show()
运行的结果:
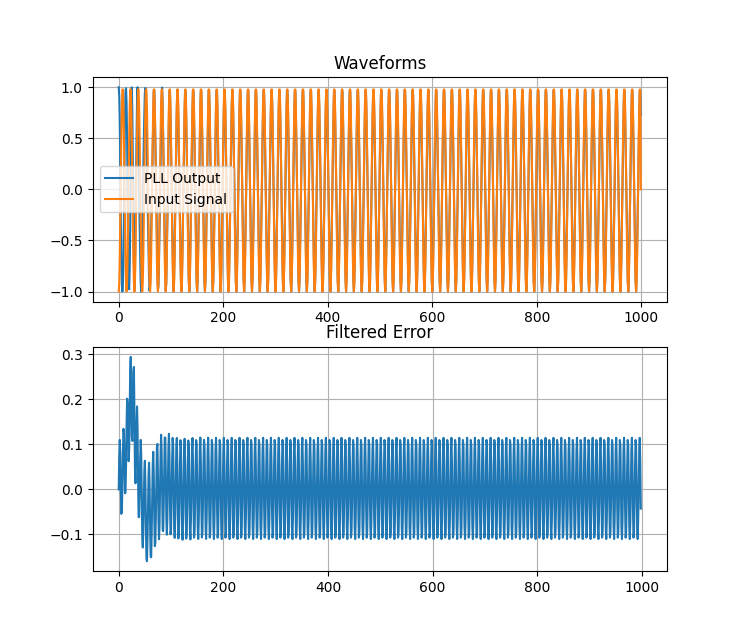

























 496
496

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










