抛物样条曲线（最详细简单的解析）

前言

抛物样条曲线是计算机曲线绘制中的一个重要的基础内容，但是很多教材和网课上对于这一部分的内容都是直接不说原因地给出大量公式，就直接劝退了包括我在内的很多小伙伴。那么今天我就通过我的理解和认识，用尽可能容易理解的方式与大家谈一谈抛物样条曲线这一部分的内容，希望能帮到大家。

1.抛物样条曲线要解决一个什么问题？

在学习抛物样条曲线之前，首先我们来思考一下关于抛物样条曲线，我们需要解决的问题是什么？
我们想要解决的问题是：对于平面中的n个点P1、P2…Pn，如何作出一条光滑的曲线，使得这条曲线能够经过上面所有的顶点。
如果大家之前学习过数值分析或者数学建模的话，应该可以看出来，没错，这就是一个典型的插值问题，但是和一般的插值问题不同的是，要求所构造的曲线要满足光滑的条件。
所谓光滑，就是曲线不能出现拐点，在每一个地方都要圆滑过渡，更加详细的定义其实就是高数中曲线的连续性。
那么问题就来了，想一想也可以知道，这么多的点，哪里去找一条这样的曲线刚好通过所有点呢？且不说工作量，单是最后得出的曲线的复杂程度就让人望而生畏。
所以就诞生了这么一种思想，那就是：我不去一次性构造出来一条完整曲线，而是每次取出一些点，构造一部分曲线，最终的曲线就是把每一次构造的小曲线连接在一起获得的。这不就是利用了算法中分而治之的思想吗！
那么，如何构造每一段小的曲线呢？要知道，构造每一段小的曲线不仅是对这一段进行插值，还要满足与下一段构造的曲线圆滑连接。
我们想到的最简单的方法就是把每一小段曲线设置为二次函数，也就是抛物线，因为相对来说，多项式函数是一种最为简单的函数，而抛物线又是次数最低的能满足曲线要求的多项式（一次多项式都是直线了，当然不行）。
因此，我们得出这样的结论：抛物样条曲线，就是将多段抛物线进行光滑连接所得到的一条完整曲线，用于得出一条通过给定的一系列点的光滑曲线。

2.分段的参数化曲线构造

我们首先来看一般的二次曲线，也就是抛物线的方程是y=ax²+bx+c，x∈[x1,x2]。
如果我们设置一个变量t，令t=(x-x1)/(x2-x1)，那我们就可以将原先的抛物线转化为另一个形式：y=A2t²+A1t+A0，t∈[0,1]。通过这样一个表达式我们可以知道，经过这样一个过程后，所得到的曲线仍然是抛物线没有变，但是自变量的取值范围从[x1,x2]转化到了[0,1]，这对我们接下来的分析很有帮助。将自变量的取值范围化归到[0,1]的这个过程就叫做规范化，得到的曲线称为参数化曲线。

由于有三个点才能构造一条抛物线，因此我们按照先后顺序假设三个点P1(x1,y1)，P2(x2,y2)和P3(x3,y3)，那么构造出来的抛物线的自变量的取值范围就是[x1,x3]。
接着，我们按照上面的方法将这三点生成的抛物线进行规范化，则可以分别得到P1对应的t1=0，P3对应的参数t3=1。
可是P2的参数还不能确定，因此我们这里令P2的参数为0.5。可能这里有小伙伴就会觉得奇怪了：并没有说P2是P1和P3的中点啊，为什么它的参数就是0.5呢？这是因为，我们上述对抛物线的规范化过程，只是为了说明任何一条抛物线都可以写成规范化的形式，并不是说只能采用这种形式进行规范化，因此，可以认为存在某一种规范化方式，使得P2点所对应的参数就是0.5（现在就这么简单理解吧，实际上0.5就是为了满足在两端点连续）。
接下来我们以三个点的坐标为已知量，抛物线的三个系数为未知量，可以得到一个三元一次方程，求解这个三元一次方程并进行同类项合并就可以得出下面的式子。

解释一下这里为什么用p表示：p表示这个点的各个坐标：比如对于平面上的一个点，就有x(t)=(1-3t+2t²)x1+(4t-4t²)x2+(-t+2t²)x3，并且有y(t)=(1-3t+2t²)y1+(4t-4t²)y2+(-t+2t²)y3。而用p(t)表示就可以只用一个式子，更加方便了。
接下来我们来观察一下这个方程，可以看出这个方程其实表达了这样一个内容：给定任意三个点的坐标，就可以按照上面的公式作出一条特殊的连接这三个点的抛物线，接下来，我们就把这样的抛物线作为我们每次每一小段插值所用的曲线。

3.完整曲线的构造

如果有n个点P1,P2…Pn，那么我们就可以分别对P1P2P3，P2P3P4…Pn-2Pn-1Pn分别按照上面的公式作出一段抛物线，总共可以构造n-2段抛物线。
用Si(ti)表示起点为Pi的那一段抛物线，其中ti表示第i段抛物线的自变量t。
可是这样我们会发现，相邻的两段抛物线之间是会发生区间重合的，比如由P1P2P3构成的抛物线和由P2P3P4构成的抛物线，中间的P2P3就会发生区间重合，如下图所示：

由于有区间重合，但是重合区间上的曲线并不重合，而我们想要的是一条连接所有点的光滑曲线，因此现在显然还不够。
但是，由于P2P3段无论是使用P1P2P3段的抛物线方程，还是P2P3P4段的抛物线方程，其实都是正确的，因此我们的想法是“各自用一部分”。
那如何做到“各自用一部分”呢？就像生物会遗传父母两边的基因一样，我们需要构造一条新曲线，只要这条曲线同时体现出P1P2P3和P2P3P4两条抛物线的特点就可以。
具体的做法是进行加权平均，假设P1P2P3这条抛物线在新的曲线中的权重为f(T)，而P2P3P4这条曲线在新的曲线中的权重为g(T)，那么就会有f(T)+g(T)=1。
假设我们新构造的P2P3段的二次曲线表达式为P2(t)，那么它就可以写成下面的形式：

P2(t)=（1-T）S1(t1)+TS(t2)

我们观察一下这个方程，方程的变量仍然是t，但是方程里面有T,t1,t2三个未知量，这怎么解决呢？这就需要将这几个未知量统一用t来进行表示。
我们通过观察可以知道t2和t1之间其实是存在关系的，这个关系就是，在P2P3段上的一个点，如果其在第一段抛物线上的参数为t1，那么其在第二段抛物线上的参数就是t1-0.5：比如P2P3上一个点在第一段抛物线P1P2P3上对应的参数为0.7，那么该点在第二段抛物线上对应的参数就是0.7-0.5=0.2，所以可以把t1和t2统一参数进行表示。
接下来，我们再进行一个假设，这个假设是：位于P2P3上不同位置的点，两条原始抛物线的权重也是不同的：我们认为越靠近左边的点，第一条抛物线P1P2P3所占的权重就越大，越靠近右边的点，第二条抛物线P2P3P4所占的权重就越大。假设权重随位置变化是线性的，则对第i条新抛物线，我们可以构造出这样一个式子：

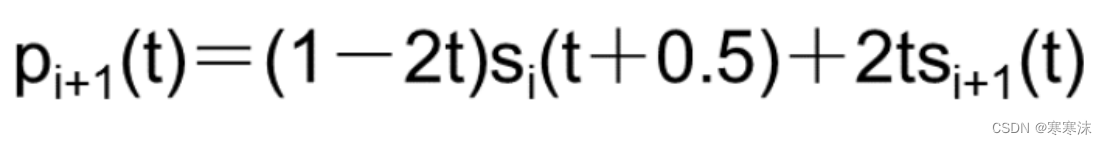
这样的一个式子中，的确只含有一个参数t了，但是如何理解这样一个式子呢？我们不妨取一些t值，取一些点进行实验。当t=0时，也就是在点P1处，得到的结果就是第一条抛物线，也就是在P1处的新抛物线就是第一条抛物线；当t=1时，也就是在点P3处，得到的结果就是第二条抛物线，也就是在P3处的新抛物线就是第二条抛物线。通过取一系列不同的t值我们可以发现：当t越大，点越靠近右端点P3，此时抛物线P2P3P4对新抛物线的影响越大；当t越小，点越靠近左端点P2，此时抛物线P1P2P3对新抛物线的影响越大。因此就满足了我们上述提出的权重随位置变化的假设！
同时我们发现，这个式子也满足了t1和t2之间的代数关系，因此我们可以认为这就是我们想要找的一条曲线的方程，就是它了！
这条新的曲线经过化简之后的结果为：
**

Pi+1(t)=(-4t³+4t²-t)Pi+(12t³-10t²+1)Pi+1+(-12t³+8t²+t)Pi+2+(4t³-2t²)Pi+3，t∈[0,0.5]

**
这样，我们对于任意四个连续的型值点Pi，Pi+1，Pi+2，Pi+3，都可以在Pi+1和Pi+2之间构造出这样的一条令我们满意的抛物线。如何称得上令我们满意？因为这条抛物线在每一段上都足够简单并且正确。
那我们是不是就完成了呢？不是的。我们想做的事情是对于给定的n个点，用一条光滑曲线将这些点连接起来，但是通过上面的方法，对于给定的n个点，我们只能作出n-3段抛物线（比如给P1P2P3P4四个点，只能作出P2P3这一段的抛物线）。
我们的优化措施是人为添加一些辅助点，因为加上辅助点之后我们可以连接更多段的抛物线。
有两种常用的加辅助点的方法。
第一种是加上两个点P0和Pn+1，令P0=P1，Pn+1=Pn，这样就可以得到一条不闭合的自由曲线。
第二种方法是加上三个辅助点P0，Pn+1和Pn+2，然后令P0=Pn，Pn+1=P1，Pn+2=P2，这样可以得到一条闭合的曲线。

这样，我们就获得了一条能够光滑连接各个点的抛物样条曲线了！