LDA主题模型学习笔记4：求解模型参数(M-step)

这一步，我们根据E-step得到的$\gamma,\phi$，最大化$L(\gamma,\phi;\alpha,\beta)$，得到$\alpha,\beta$.

1，拉格朗日乘数法求解$\beta$

     首先把$L(\gamma,\phi;\alpha,\beta)$简化，只保留与$\beta$有关的部分。因为$\beta$是每一行存一个主题的词分布，所以每一行的和是1，存在等式约束$\sum_{j=1}^V\beta_{ij}=1$，所以是带等式约束的最大化问题，使用拉格朗日乘数法，可得到拉格朗日函数如下：

用拉格朗日函数对$\beta$求偏导，令偏导为0，可得：

     这里的$\phi_{dni}$指的是对第d个文档的变分参数$\phi_{ni}$，也就是第n个单词在第i个主题的词分布中的概率，$w_{dn}^j$是第d个文档中第n个单词$w_n$，$w_n$是一个V维向量，其中只有一个元素是1，其他都是0，这个为1的元素对应的索引号就是这个单词在文档集字典中的ID，上标j是指$w_n$向量中的每个元素，如果$w_{dn}^j=1$那么单词$w_n$在文档集字典中的ID就是j。

2，牛顿法求解$\alpha$

首先把$L(\gamma,\phi;\alpha,\beta)$简化，只保留与$\alpha$有关的部分：

因为$\alpha$是Dirichlet分布的参数(K维的，K是主题个数)，所以它没有约束条件，直接对$\alpha$求偏导：

     可以看到，一阶导数的结果中包含$\alpha_j$，这里不能直接令偏导为0解出$\alpha$。所以需要考虑迭代的方法去求解，作者在这里使用牛顿迭代法。牛顿法的理解可以参考这里：http://blog.csdn.net/luoleicn/article/details/6527049
对于K维向量$\alpha$，它的牛顿迭代式如下：

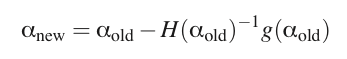
     其中$H(\alpha),g(\alpha)$分别是$\alpha$处的Hessian矩阵和梯度。这里我们可以看到有对Hessian矩阵求逆的操作，这个操作时间复杂度高达$O(n^3)$，所以考虑简化这个求逆操作。
Hessian矩阵的元素是：

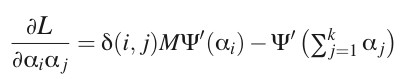
首先对Hessian矩阵H进行分解：

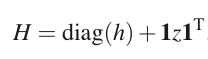
这样Hessian矩阵的逆就成了如下形式：

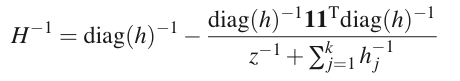
对于$\alpha$的第i个分量，Hessian矩阵的逆和梯度的乘积：

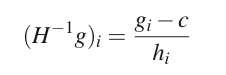
其中：

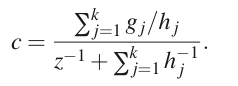
这样可以看到，$(H^{-1}g)_i$只与$h_i$和$g_i$有关，它们的值各有k个，所以这时的牛顿法是线性的。

---

本文内容来自LDA原始论文《Latent Dirichlet Allocation》的附录A.2, A.4.