【推荐算法】FM模型：Factorization Machines

1、线性回归

在介绍FM之前，我们先简单回顾以下线性回归。

回归分析是一种预测性的建模技术，它研究的是因变量（目标）和自变量（预测器）之间的关系。这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系。通常使用曲线/直线来拟合数据点，目标是使曲线到数据点的距离差异最小。

线性回归是回归问题中的一种，线性回归假设目标值与特征之间线性相关，即满足一个多元一次方程。通过构建损失函数，来求解损失函数最小时的参数w和b。通常我们可以表达成如下公式：

为预测值，自变量x和因变量y是已知的，而我们想实现的是预测新增一个x，其对应的y是多少。因此，为了构建这个函数关系，目标是通过已知数据点，求解线性模型中w和b两个参数。

求解最佳参数，需要一个标准来对结果进行衡量，为此我们需要定量化一个目标函数式，使得计算机可以在求解过程中不断地优化。针对任何模型求解问题，都是最终都是可以得到一组预测值，对比已有的真实值y，数据行数为n，可以将损失函数定义如下：

即预测值与真实值之间的平均的平方距离，统计中一般称其为MAE(mean square error)均方误差。把之前的函数公式代入损失函数，并且将需要求解的参数w和b看做是函数L的自变量，可得：

现在的任务是求解最小化L时w和b的值，因此核心目标优化式转化为：

该问题的求解方式有两种：

• 最小二乘法(least square method)

求解w和b是使损失函数最小化的过程，在统计中，称为线性回归模型的最小二乘“参数估计”(parameter estimation)。我们可以将L(w,b)分别对w和b求导，得到：

令上述两式为0，可得到w和b最优解的闭式(closed-form)解：

• 梯度下降(gradient descent)

梯度下降核心内容是对自变量进行不断的更新（针对w和b求偏导），使得目标函数不断逼近最小值的过程：

这里多说一下线性回归与逻辑回归，逻辑回归是在线性回归的基础上多了一个sigmoid变换，具体的判别模型如下：

---

2、FM模型

FM算法是一种基于矩阵分解的机器学习算法，是为了解决大规模稀疏数据中的特征组合问题。

在传统的线性模型如LR中，每个特征都是独立的，如果需要考虑特征与特征之间的交互作用，可能需要人工对特征进行交叉组合；非线性SVM可以对特征进行kernel映射，但是在特征高度稀疏的情况下，并不能很好地进行学习；现在也有很多分解模型Factorization Model如矩阵分解MF、SVD++等，这些模型可以学习到特征之间的交互隐藏关系，但基本上每个模型都只适用于特定的输入和场景。

为此，在高度稀疏的数据场景下如推荐系统，FM（因子分解机）出现了。

FM考虑了特征之间的交互作用，并对特征进行了交叉组合。FM在线性模型的基础上添加了一个多项式，用于描述特征之间的二阶交叉（FM也支持多阶，本文以二阶FM为例）。

对于一个给定的特征向量，线性回归的模型函数为：

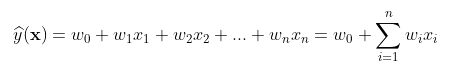
其中，和为模型参数，特征分量和之间是相互独立的，即中仅考虑了单个的特征分量，而没有考虑特征分量之间的关系。为了表述特征之间的相互关系，在线性模型的基础上添加一个多项式，特征和的组合用