股票量化交易软件：利用卡尔曼 (Kalman) 滤波器预测价格方向

导言

货币和股票价格的图表总是包含价格波动, 其频率和幅度有所不同。我们的任务是判断基于这些短期和长期走势的主要趋势。一些交易者在图表上绘制趋势线, 而另一些人则使用指标。在这两种情况下, 我们的目的是将真正的价格走势从受到次要因素影响而导致的噪音中分离出来, 因为噪音只会产生短期效果。在本文中, 赫兹量化交易软件提议利用卡尔曼滤波器将主要走势与市场噪音分开。

在交易中使用数字滤波器的思路并不鲜见。例如, 我曾 描述过 运用低通滤波器。但追求完美是无止境的, 所以我们再考察一个策略, 比较一下结果。

1. 卡尔曼滤波器原理

那么, 什么是卡尔曼滤波器, 为什么我们感兴趣呢？以下过滤器定义来自 维基百科 :

卡尔曼滤波器 是一种使用一系列随时间观测到的测量值的算法, 包含统计噪声和其它不准确性。

这意味着该滤波器最初是为处理噪声数据而设计的。还有, 它能够处理不完整的数据。另一个优点, 它是为动态系统设计并应用的; 我们的价格图表恰好属于这样的系统。

滤波器算法的工作在两个步骤中处理:

1. 外推 (预测)
2. 更新 (校正)

1.1. 外推, 系统数值的预测

滤波器操作算法的第一阶段是利用已分析过程的基础模型。在此模型基础上, 形成单步前瞻预测。

(1.1)

其中:

• xk 是动态系统在第 k 步的外推值,
• Fk 是状态转换模型, 展体现当前系统状态对先前状态的依赖性,
• x^k-1 是系统的前一个状态 (前一步中的滤波值),
• Bk 是控制输入模型, 展现控制对系统的影响,
• uk 是系统上的控制向量。

例如, 控制效果可以是新闻因素。不过, 实际当中效果是未知的, 且被忽略, 而其影响是指噪声。

之后预测系统的协方差误差:

(1.2)

其中:

• Pk 是动态系统状态向量的外推协方差矩阵,
• Fk 是状态转换模型, 展体现当前系统状态对先前状态的依赖性,
• P^k-1 是状态向量的协方差矩阵在前一步的更新,
• Qk 是过程的协方差噪声矩阵。

1.2. 系统值的更新

滤波器算法的第二步从测量实际系统的状态 zk 开始。考虑到真实系统状态和测量误差, 指定系统状态的实际测量值。在赫兹量化交易软件的案例中, 测量误差是噪声对动态系统的影响。

此刻, 我们已有两个不同的数值代表单个动态过程的状态。它们包括第一步计算的动态系统外推值, 和实际的测量值。这些具有一定的几率度的数值, 当中的每一个均表征我们过程的真实状态, 因此, 该值介于这两个值之间。因此, 我们的目标是确定信任度, 即此值或彼值的信任程度。为此目的, 执行卡尔曼滤波器第二阶段的迭代。

利用已有数据, 我们判断实际系统状态自外推值的偏差。

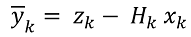
(2.1)

此处:

• yk 是外推之后系统实际状态在第 k 步的偏差,
• zk 是第 k 步中系统的实际状态,
• Hk 是显示实际系统状态对于所计算数据依赖性的测量矩阵 (在实际中经常取值一),
• xk 是动态系统在第 k 步的外推值。

在下一步中, 计算误差向量的协方差矩阵:

(2.2)

此处:

• Sk 是在第 k 步的误差矢量的协方差矩阵,
• Hk 是显示实际系统状态对于计算数据依赖性的测量矩阵,
• Pk 是动态系统状态向量的外推协方差矩阵,
• Rk 是测量噪声的协方差矩阵。

然后检测优化增益。增益反映了计算值和经验值的置信度。