前言
SLAM问题的处理方法主要分为滤波和图优化两类。滤波的方法中常见的是扩展卡尔曼滤波、粒子滤波、信息滤波等,熟悉滤波思想的同学应该容易知道这类SLAM问题是递增的、实时的处理数据并矫正机器人位姿。比如基于粒子滤波的SLAM的处理思路是假设机器人知道当前时刻的位姿,利用编码器或者IMU之类的惯性导航又能够计算下一时刻的位姿,然而这类传感器有累计误差,所以再将每个粒子的激光传感器数据或者图像特征对比当前建立好的地图中的特征,挑选和地图特征匹配最好的粒子的位姿当做当前位姿,如此往复。当然在gmapping、hector_slam这类算法中,不会如此轻易的使用激光数据,激光测距这么准,当然不能只用来计算粒子权重,而是将激光数据与地图环境进行匹配(scan match)估计机器人位姿,比用编码器之流精度高出很多。
好了,扯了很多,目光回到今天的重心图优化。目前SLAM主流研究热点几乎都是基于图优化的,在讲解之前,不免要问,为啥都用图优化了。我想这和传感器有很大关系,以前使用激光构建二维的地图,现在研究热点都是用单目、双目、RGB-D构建地图。处理视觉SLAM如果用EKF,随着时间推移地图扩大,内存消耗,计算量都很大;而使用图优化计算在高建图精度的前提下效率还快。关于filter 和 graph 两类方法在visual slam里的对比可以参见《visual slam: why filter?》,lz在这方面没有深入学习对比,希望有能力的网友能够补充。当然,不是说激光SLAM就不能用图优化,也可以,在博文中激光SLAM的图优化形式将以一个简单例子在博客中讲解。
在图优化的方法中(graph-based slam),处理数据的方式就和滤波的方法不同了,它不是在线的纠正位姿,而是把所有数据记下来,最后一次性算账。在这个graph slam tutorial系列中,还是熟悉的配方熟悉的味道,和其他从推导到应用系列博文一样将通过简单的例子,理论推导,程序应用等三个方面来介绍graph slam。如果有错误,还请指正,谢谢。
图优化是什么?
图是由节点和边构成,SLAM问题怎么构成图呢?在graph-based SLAM中,机器人的位姿是一个节点(node)或顶点(vertex),位姿之间的关系构成边(edge)。具体而言比如t+1时刻和t时刻之间的odometry关系构成边,或者由视觉计算出来的位姿转换矩阵也可以构成边。一旦图构建完成了,就要调整机器人的位姿去尽量满足这些边构成的约束。
所以图优化SLAM问题能够分解成两个任务:
1. 构建图,机器人位姿当做顶点,位姿间关系当做边,这一步常常被成为前端(front-end),往往是传感器信息的堆积。
2. 优化图,调整机器人位姿顶点尽量满足边的约束,这一步称为后端(back-end)。
图优化过程如下图所示:先堆积数据,机器人位姿为构建的顶点。边是位姿之间的关系,可以是编码器数据计算的位姿,也可以是通过ICP匹配计算出来的位姿,还可以是闭环检测的位姿关系。构建的图和原始未经优化的地图如下:
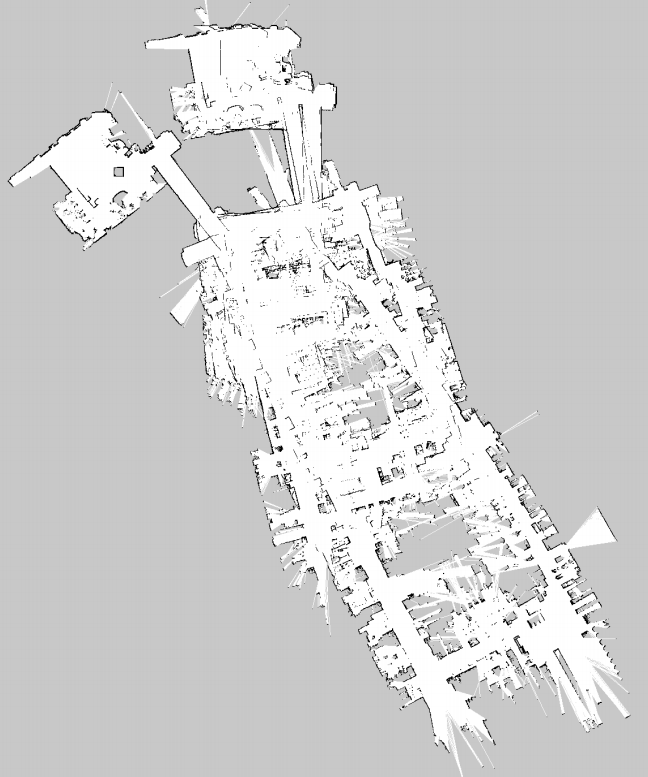
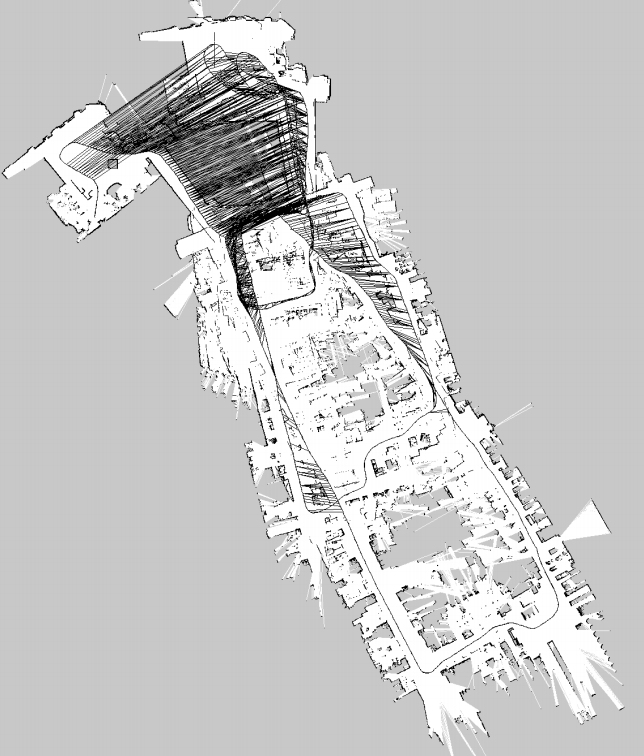
够建好图以后,就能调整顶点满足边的约束,最后得到的优化后的地图如下图右所示。
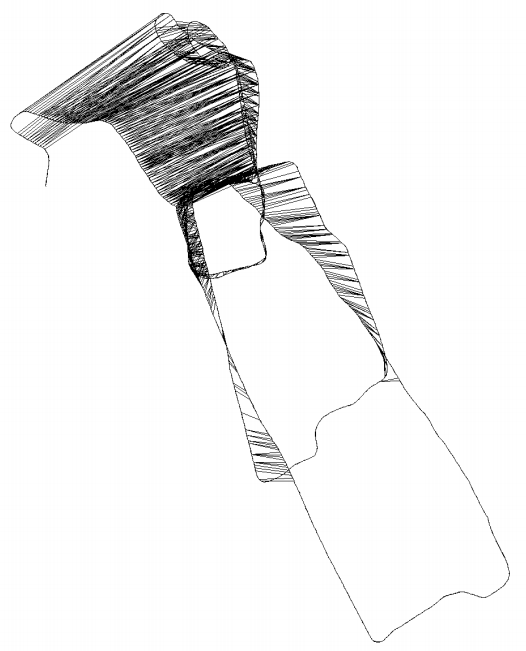
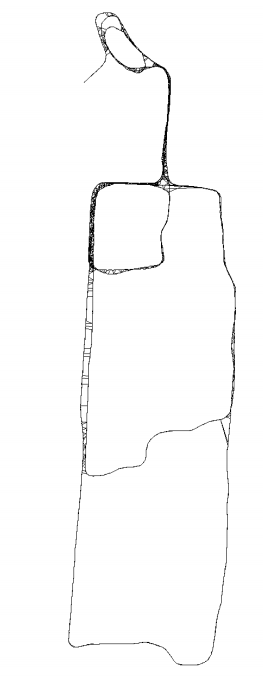
一个帮助理解的例子:
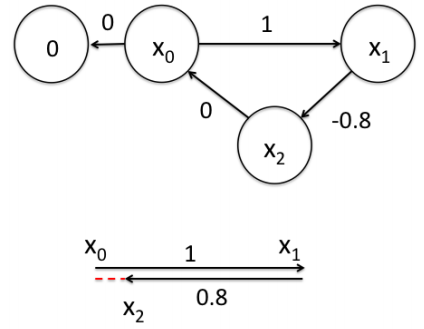
为了更好的理解这个过程,将用一个很好的例子作说明。如下图所示,假设一个机器人初始起点在0处,然后机器人向前移动,通过编码器测得它向前移动了1m,到达第二个地点。接着,又向后返回,编码器测得它向后移动了0.8米。但是,通过闭环检测,发现它回到了原始起点。可以看出,编码器误差导致计算的位姿和观测到有差异,那机器人这几个状态中的位姿到底是怎么样的才最好的满足这些条件呢?
首先构建位姿之间的关系,即图的边:
线性方程组中变量小于方程的个数,要计算出最优的结果,使出杀手锏最小二乘法。先构建残差平方和函数:
为了使残差平方和最小,我们对上面的函数每个变量求偏导,并使得偏导数等于0.
整理得到:
接着矩阵求解线性方程组:
所以调整以后为满足这些边的条件,机器人的位姿为:
在这里例子中我们发现,闭环检测起了决定性的作用。
另一个例子:
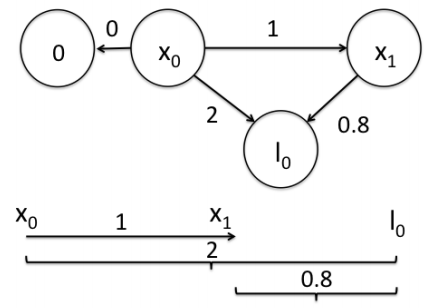
前面是用闭环检测,这次用观测的路标(landmark)来构建边。如下图所示,假设一个机器人初始起点在0处,并观测到其正前方2m处有一个路标。然后机器人向前移动,通过编码器测得它向前移动了1m,这时观测到路标在其前方0.8m。请问,机器人位姿和路标位姿的最优状态?
在这个图中,我们把路标也当作了一个顶点。构建边的关系如下:
即
残差平方和:
求偏导数:
最后整理并计算得:
得到路标和机器人位姿:
接下来,将引入了一个重要的概念。我们知道传感器的精度是有差别的,也就是说我们对传感器的相信程度应该不同。比如假设这里编码器信息很精确,测得的路标距离不准,我们应该赋予编码器信息更高的权重,假设是10。重新得到残差平方和如下:
求偏导得:
转换为矩阵:
最后计算得到:
将这个结果和之前对比,可以看到这里的机器人位姿x1更靠近编码器测量的结果。请记住这种思想,这里的权重就是在后面将要经常提到的边的信息矩阵,在后面还将介绍。
通过两个例子了解了graph based slam以后,在下一篇博文中,将对图优化的后端(back-end)进行理论推导,并结合matlab仿真程序进行编程应用。
(转载请注明作者和出处:http://blog.csdn.net/heyijia0327 未经允许请勿用于商业用途)
reference:
1. Grisetti. 《A Tutorial on Graph-Based SLAM》
2. University of Alberta 很棒的机器人课程 https://webdocs.cs.ualberta.ca/~zhang/c631/主要以作业为主,例子来源于该课程。
3. Strasdat. 《Visual SLAM: Why Filter?》
4. Grisetti. 课件 《SLAM Back-end》(可以直接搜到)
5. Rainer & Grisetti 《g2o: A General Framework for Graph Optimization》








 本文探讨了SLAM问题中图优化方法的应用,详细解释了图构建与优化的过程,并通过实例展示了如何解决机器人位姿估计问题。文章还强调了图优化在视觉SLAM中的优势及与其他方法的对比。
本文探讨了SLAM问题中图优化方法的应用,详细解释了图构建与优化的过程,并通过实例展示了如何解决机器人位姿估计问题。文章还强调了图优化在视觉SLAM中的优势及与其他方法的对比。
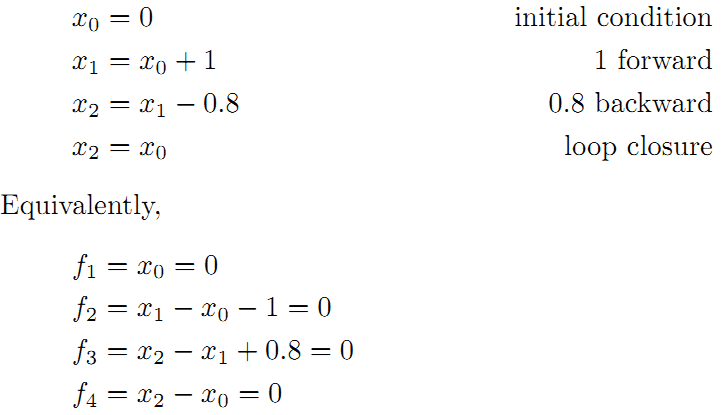
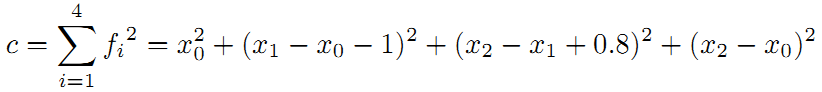
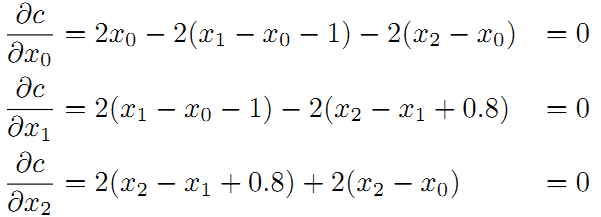
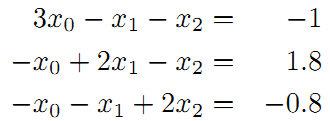
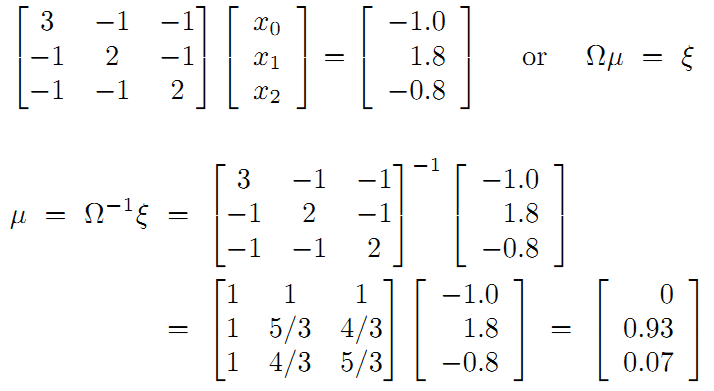
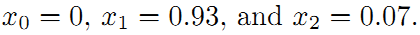

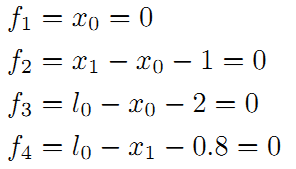

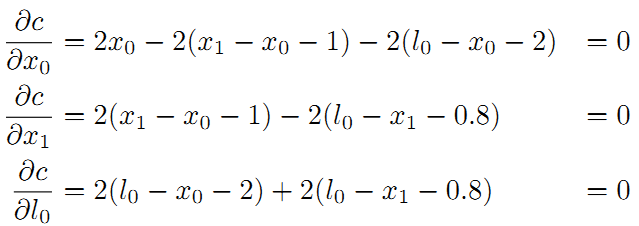
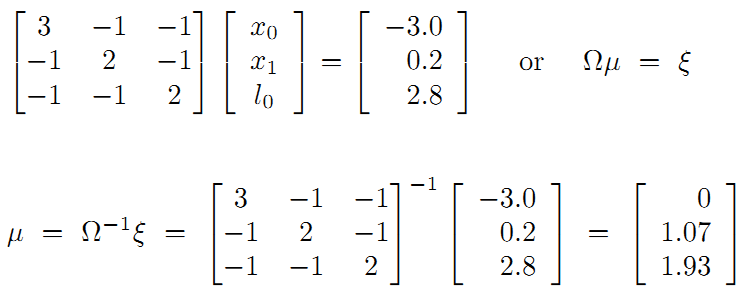
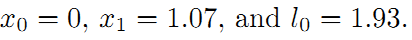
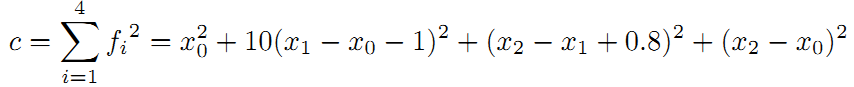
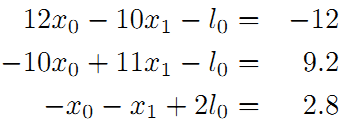
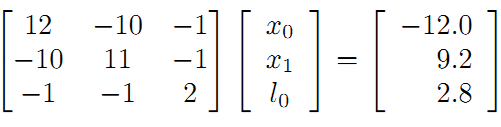

















 5641
5641

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








