行列式(直观几何)
det: delta : 希腊字母表中第4个字母,相当于英语字母中的d,通常含义是 变化量 、变化了多少
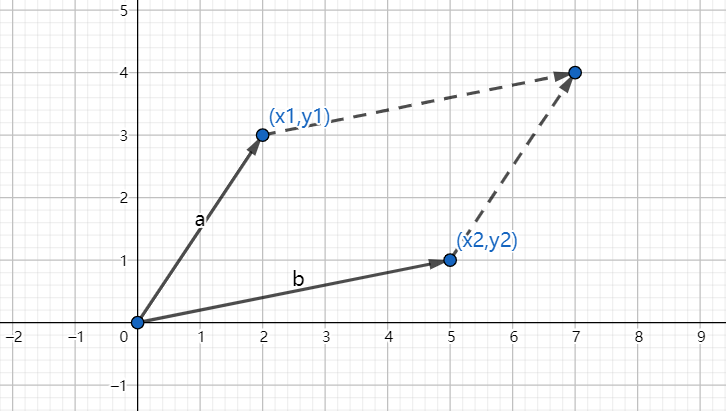
上图中 向量a和向量b围城的平行四边形 用矩阵A表示,如下:
A = [ x 1 y 1 x 2 y 2 ] A=\begin{bmatrix} x_{1} & y_{1} \\ x_{2} & y_{2} \\ \end{bmatrix} A=[x1x2y1y2]
det (A) 字面意思就是 从向量a到向量b变化了多少, 确切定义是 矩阵A代表的平行四边形的面积.
正因为从向量a到向量b是有变化的,所以向量a和向量b围成的平行四边形才有面积
如果从向量a到向量b没有变化(向量a和向量b重合), 则向量a和向量b围成的平行四边形面积为0.
所以 行列式 才叫 det
高等代数(上)
符号约定、用词约定
线性代数 符号约定、用词约定
A A A : 矩阵
det(A) : 矩阵A的行列式, 为一实数
E n E_{n} En 或 I n I_{n} In : 单位阵,n行n列的单位方阵
μ k , i \mu_{k,i} μk,i : 矩阵的第k行第i列元素的余子阵,为一更小的矩阵
1.4 行列式
行列式 由余子阵递归定义
行列式的定义是递归定义
矩阵A是n行n列的方阵,
矩阵A中的第k行第i列元素记为 a k , i a_{k,i} ak,i,
A = [ a 1 , 1 a 1 , 2 . . . a 1 , i . . . a 1 , n a 2 , 1 a 2 , 2 . . . a 2 , i . . . a 2 , n . . . . . . . . . . . . . . . . . . a k , 1 a k , 2 . . . a k , i . . . a k , n . . . . . . . . . . . . . . . . . . a n , 1 a n , 2 . . . a n , i . . . a n , n ] A=\begin{bmatrix} a_{1,1} & a_{1,2} & ... & a_{1,i} & ... & a_{1,n} \\ a_{2,1} & a_{2,2} & ... & a_{2,i} & ... & a_{2,n} \\ ... & ... & ... & ... & ... & ... \\ a_{k,1} & a_{k,2} & ... & a_{k,i} & ... & a_{k,n} \\ ... & ... & ... & ... & ... & ... \\ a_{n,1} & a_{n,2} & ... & a_{n,i} & ... & a_{n,n} \\ \end{bmatrix} A=⎣⎢⎢⎢⎢⎢⎢⎡a1,1a2,1...ak,1...an,1a1,2a2,2...ak,2...an,2..................a1,ia2,i...ak,i...an,i..................a1,na2,n...ak,n...an,n⎦⎥⎥⎥⎥⎥⎥⎤
矩阵A中去掉第k行和第i列 ,余下的元素组成的矩阵,称为原矩阵A的余子阵 μ k , i \mu_{k,i} μk,i
μ k , i = [ a 1 , 1 a 1 , 2 . . . a 1 , i − 1 a 1 , i + 1 . . . a 1 , n a 2 , 1 a 2 , 2 . . . a 2 , i − 1 a 2 , i + 1 . . . a 2 , n . . . . . . . . . . . . . . . . . . . . . a k − 1 , 1 a k − 1 , 2 . . . a k − 1 , i − 1 a k − 1 , i + 1 . . . a k − 1 , n a k + 1 , 1 a k + 1 , 2 . . . a k + 1 , i − 1 a k + 1 , i + 1 . . . a k + 1 , n . . . . . . . . . . . . . . . . . . . . . a n , 1 a n , 2 . . . a n , i − 1 a n , i + 1 . . . a n , n ] \mu_{k,i}=\begin{bmatrix} a_{1,1} & a_{1,2} & ... & a_{1,i-1} & a_{1,i+1} & ... & a_{1,n} \\ a_{2,1} & a_{2,2} & ... & a_{2,i-1} & a_{2,i+1} & ... & a_{2,n} \\ ... & ... & ... & ... & ... & ... & ... \\ a_{k-1,1} & a_{k-1,2} & ... & a_{k-1,i-1} & a_{k-1,i+1} & ... & a_{k-1,n} \\ a_{k+1,1} & a_{k+1,2} & ... & a_{k+1,i-1} & a_{k+1,i+1} & ... & a_{k+1,n} \\ ... & ... & ... & ... & ... & ... & ... \\ a_{n,1} & a_{n,2} & ... & a_{n,i-1} & a_{n,i+1} & ... & a_{n,n} \\ \end{bmatrix} μk,i=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡a1,1a2,1...ak−1,1ak+1,1...an,1a1,2a2,2...ak−1,2ak+1,2...an,2.....................a1,i−1a2,i−1...ak−1,i−1ak+1,i−1...an,i−1a1,i+1a2,i+1...ak−1,i+1ak+1,i+1...an,i+1.....................a1,na2,n...ak−1,nak+1,n...an,n⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
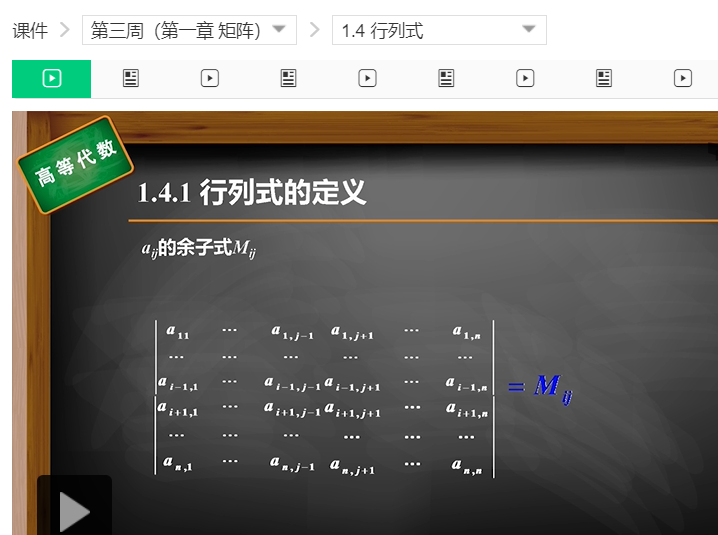
例如,将矩阵A按第一行元素的余子阵展开,则有 矩阵A的行列式det(A)定义为:
d e t ( A ) = ∑ i = 1 n a 1 , i ( − 1 ) 1 + i d e t ( μ 1 , i ) det(A)=\sum_{i=1}^{n} a_{1,i}(-1)^{1+i}det(\mu_{1,i}) det(A)=∑i=1na1,i(−1)1+idet(μ1,i)
可见,行列式定义显然是递归的: 矩阵A的行列式由多个更小的矩阵的行列式定义的, 这些更小的矩阵就是原矩阵A的余子阵。
显然,
可以将矩阵A按任一行的余子阵 展开,来定义矩阵A的行列式det(A), 如下:d e t ( A ) = ∑ i = 1 n a k , i ( − 1 ) k + i d e t ( μ k , i ) , ∀ k ∈ { 1 , 2 , . . . , n } det(A)=\sum_{i=1}^{n} a_{k,i}(-1)^{k+i}det(\mu_{k,i}), {\forall}k \in \{1,2,...,n\} det(A)=∑i=1nak,i(−1)k+idet(μk,i),∀k∈{1,2,...,n}
可以将矩阵A按任一列的余子阵 展开,来定义矩阵A的行列式det(A),如下:
d e t ( A ) = ∑ k = 1 n a k , i ( − 1 ) k + i d e t ( μ k , i ) , ∀ i ∈ { 1 , 2 , . . . , n } det(A)=\sum_{k=1}^{n} a_{k,i}(-1)^{k+i}det(\mu_{k,i}), {\forall}i \in \{1,2,...,n\} det(A)=∑k=1nak,i(−1)k+idet(μk,i),∀i∈{1,2,...,n}
余子阵 μ k , i \mu_{k,i} μk,i的行列式 d e t ( μ k , i ) det(\mu_{k,i}) det(μk,i)称为余子式 , 又记为 M k , i M_{k,i} Mk,i
( − 1 ) k + i d e t ( μ k , i ) (-1)^{k+i}det(\mu_{k,i}) (−1)k+idet(μk,i)称为代数余子式, 又记为 A k , i A_{k,i} Ak,i,
即 A k , i = ( − 1 ) k + i M k , i A_{k,i}=(-1)^{k+i}M_{k,i} Ak,i=(−1)k+iMk,i
不确定,线性代数教材中有没有余子阵的叫法,但有余子式。
但显然应该有余子阵的叫法,才是合理的。
线性代数
伴随矩阵 中的每个元素都是余子式
伴随矩阵 A ∗ A^{*} A∗ 中的每个元素都是余子式 d e t ( μ k , i ) det(\mu_{k,i}) det(μk,i)
逆矩阵 的 行列式倍 为 伴随矩阵
逆矩阵 A − 1 A^{-1} A−1 为 1 d e t ( A ) \dfrac{1}{det(A)} det(A)1 倍 伴随矩阵 A ∗ A^{*} A∗ 即 : A ∗ ∗ A = d e t ( A ) I n A^{*} * A=det(A) I_{n} A∗∗A=det(A)In
线性代数重学(七月在线)
线性代数(七月在线)课件?
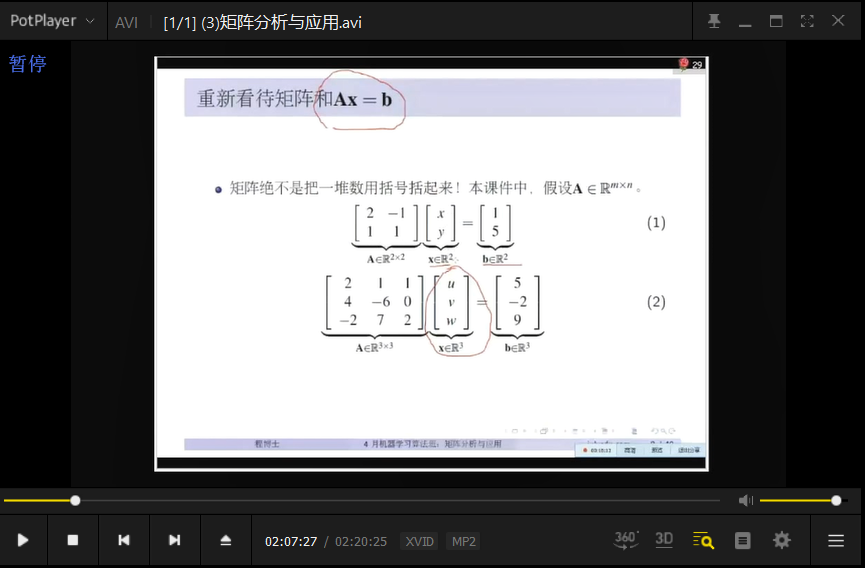
线性代数 中的 维 和 物理中的 维 不一样
线性代数中的 矩阵 只是简单的加一行, 就多了一维。
但物理中,简单的加一行 并不是一个维?(所以物理中的维是啥?)
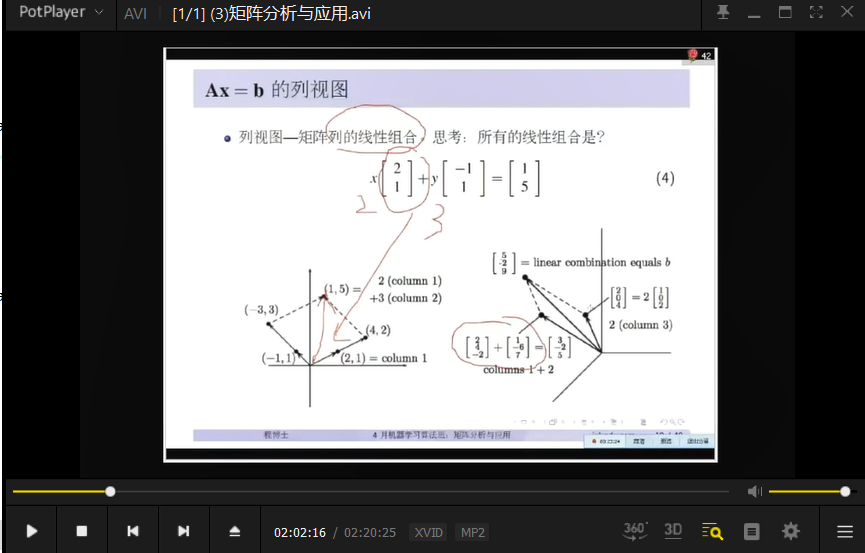
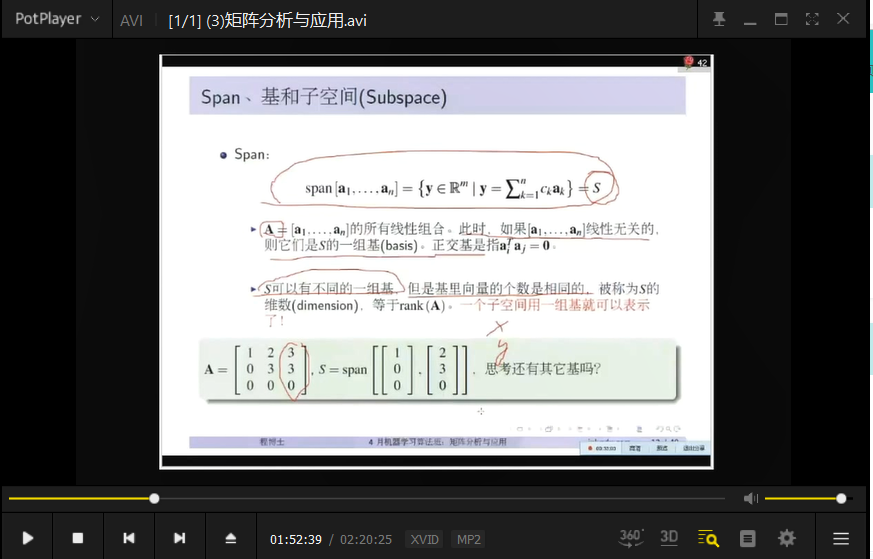
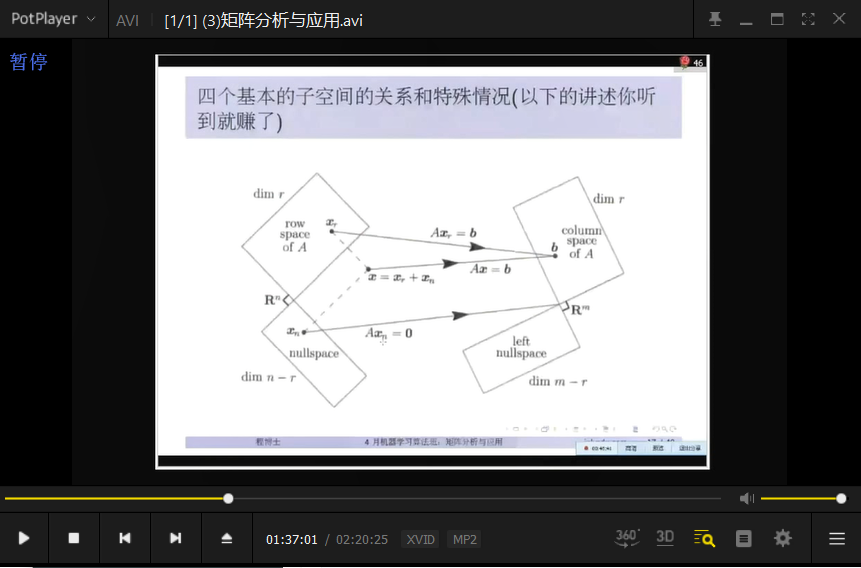
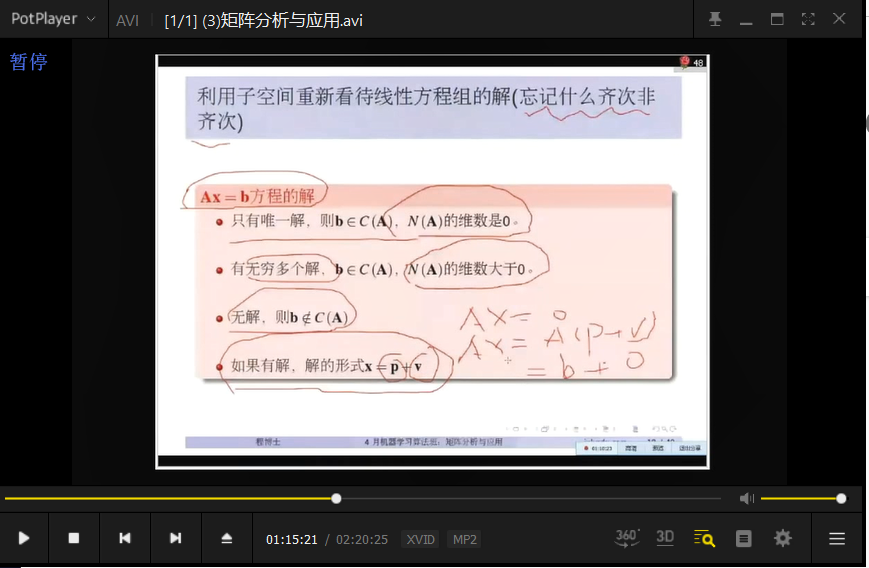
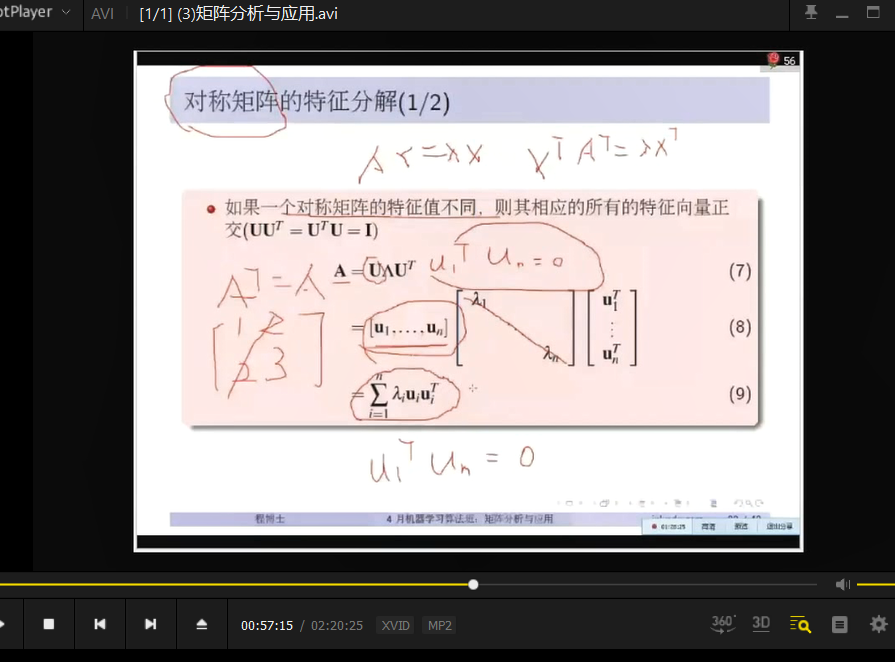
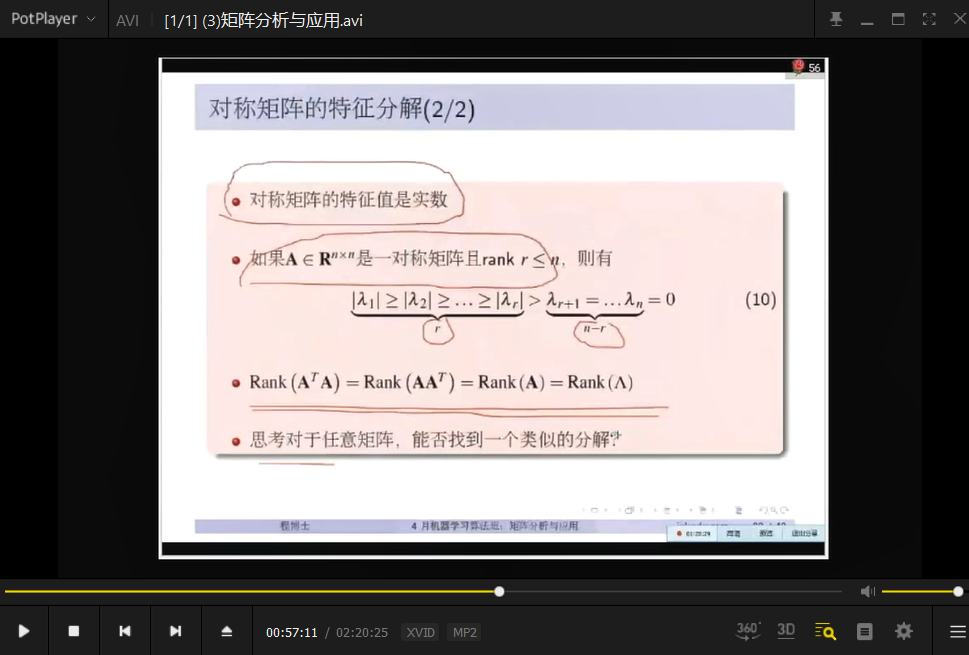
矩阵的行秩 、矩阵的列秩
矩阵的行秩: 从 该矩阵全部行向量 找不相关的行向量, 能找到的 不相关的 行向量 的 最多个数。
矩阵的列秩: 从 该矩阵全部列向量 找不相关的列向量, 能找到的 不相关的 列向量 的 最多个数。
矩阵的行秩和列秩为何相等?
之所以 矩阵的行秩 和 列秩 相等, 是因为:
- 对一个矩阵增加一行时,若该行导致行秩增加一,则该行也同样导致列秩增加一
- 对一个矩阵增加一列时,若该列导致列秩增加一,则该列也同样导致行秩增加一
- 而任意一个矩阵都可以从最小矩阵[1]开始, 经过若干次增加行或列的方式来到达
所以 矩阵的行秩 和 列秩 相等
由此可见,矩阵的行秩和列秩相等,实际是个递归问题。
线性代数(3blue1brown)
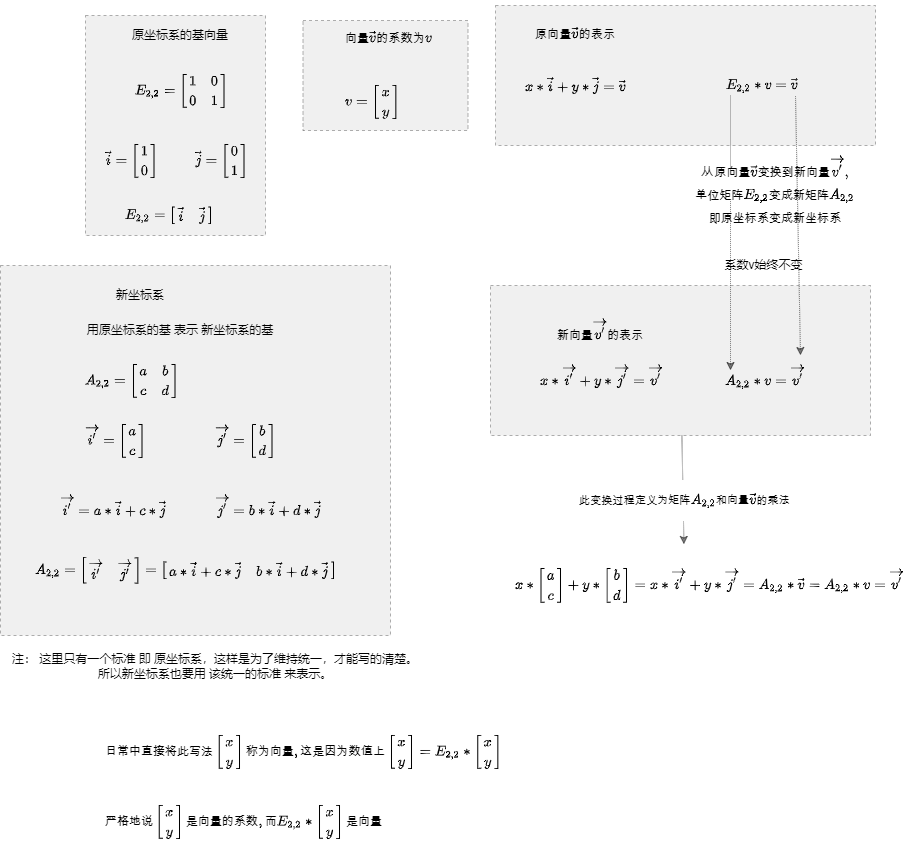
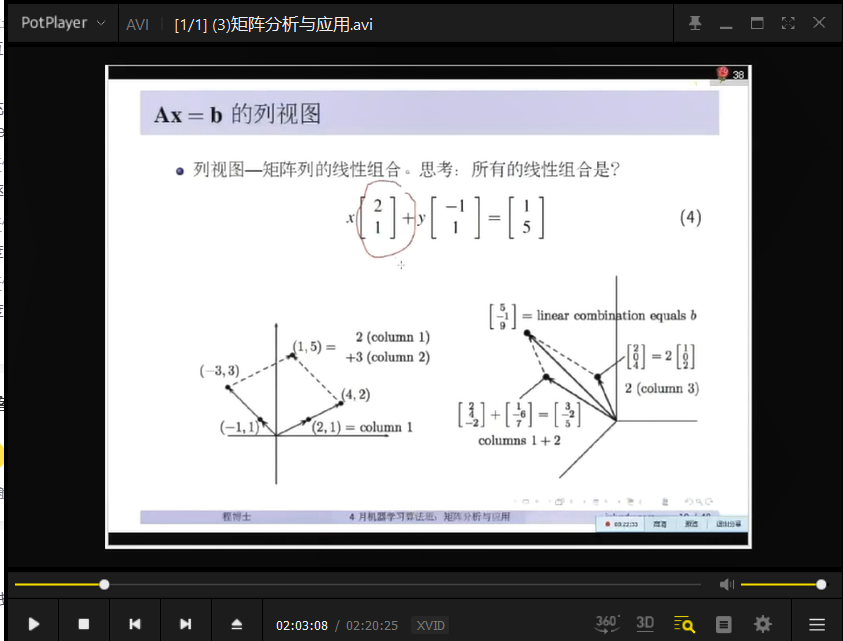
七月在线 (3)矩阵分析与应用.avi
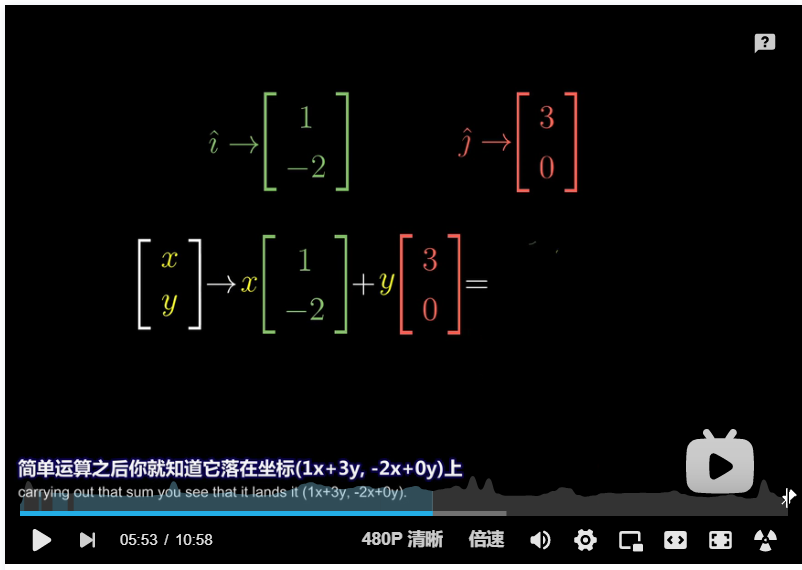
原 坐 标 基 向 量 : i ⃗ = [ 1 0 ] , j ⃗ = [ 0 1 ] 经 过 矩 阵 A 变 换 后 的 坐 标 基 向 量 : i ′ ⃗ = [ a b ] , j ′ ⃗ = [ c d ] 变 换 即 : i ⃗ → i ′ ⃗ , j ⃗ → j ′ ⃗ 变 换 即 : i ′ ⃗ = a i ⃗ + b j ⃗ , j ′ ⃗ = c i ⃗ + d j ⃗ , 完 全 用 原 坐 标 基 向 量 来 描 述 , 才 不 混 乱 向 量 变 换 即 : x i ⃗ + y j ⃗ → x i ′ ⃗ + y j ′ ⃗ 变 换 即 : 矩 阵 A = [ a c b d ] = [ i ′ ⃗ , j ′ ⃗ ] 但 是 这 貌 似 仅 仅 对 于 方 阵 A 而 言 ? \tiny 原坐标基向量: \small \vec{i}=\begin{bmatrix} 1 \\ 0 \\ \end{bmatrix}, \vec{j}=\begin{bmatrix} 0 \\ 1 \\ \end{bmatrix}\\ \tiny 经过矩阵A变换后的坐标基向量: \small \vec{i'}=\begin{bmatrix} a \\ b \\ \end{bmatrix}, \vec{j'}=\begin{bmatrix} c \\ d \\ \end{bmatrix}\\ \tiny 变换即: \small \vec{i} \rightarrow \vec{i'}, \vec{j} \rightarrow \vec{j'}\\ \tiny 变换即: \small \vec{i'}=a \vec{i} + b \vec{j} , \vec{j'}=c \vec{i} + d \vec{j} , \tiny{ 完全用原坐标基向量来描述,才不混乱} \\ \tiny 向量变换即: \small x \vec{i} + y \vec{j} \rightarrow x \vec{i'} + y \vec{j'}\\ \tiny 变换即: 矩阵 \small A=\begin{bmatrix} a & c \\ b & d \\ \end{bmatrix}=[\vec{i'}, \vec{j'}]\\ \tiny 但是这貌似仅仅对于方阵A而言? 原坐标基向量:i=[10],j=[01]经过矩阵A变换后的坐标基向量:i′=[ab],j′=[cd]变换即:i→i′,j→j′变换即:i′=ai+bj,j′=ci+dj,完全用原坐标基向量来描述,才不混乱向量变换即:xi+yj→xi′+yj′变换即:矩阵A=[abcd]=[i′,j′]但是这貌似仅仅对于方阵A而言?
非 方 阵 维 度 缩 减 二 维 变 一 维 变 换 即 : i ′ ⃗ = a i ⃗ + 0 j ⃗ , j ′ ⃗ = c i ⃗ + 0 j ⃗ , 用 系 数 0 消 掉 原 基 分 量 j ⃗ \\ \tiny 非方阵 维度缩减 二维变一维\\ \tiny 变换即: \small \vec{i'}=a \vec{i} + 0 \vec{j} , \vec{j'}=c \vec{i} + 0 \vec{j} , \tiny 用系数0消掉 原基分量 \small \vec{j} \\ 非方阵维度缩减二维变一维变换即:i′=ai+0j,j′=ci+0j,用系数0消掉原基分量j
非 方 阵 维 度 增 加 二 维 变 三 维 怎 么 写 ? 变 换 即 : i ′ ⃗ = ? , j ′ ⃗ = ? , \\ \tiny 非方阵 维度增加 二维变三维 怎么写?\\ \tiny 变换即: \small \vec{i'}=? , \vec{j'}=?, \\ 非方阵维度增加二维变三维怎么写?变换即:i′=?,j′=?,






















 7845
7845











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










