散射矩阵、协方差矩阵
数学基础 2009-09-03 15:39:35 阅读180 评论0 字号:大中小
散射矩阵,又称S矩阵,是物理学中描述散射过程的一个主要观测量。
现代高能物理的发展,同其他物理学一样是理论和实验的互动,而这种互动主要的桥梁就是散射矩阵。
假设散射源为很好的定域散射源,与被散射粒子的相互作用局限在有限的空间范围内,那么,无穷远时间以前粒子处于一个自由态,称为入态,记为|Ψ>in;无穷远时间之后粒子也是处于一个自由态,称为出态,记为|Ψ>out。 入态到初态,相互作用可以用一个矩阵描述,记为S,那么就有:
|Ψ>out=S |Ψ>in
这就是散射矩阵的定义。
散射矩阵直接与可观测的物理量相联系,但是我们在量子场论中处理的是场,两者如何联系?或者说如何从量子场论计算散射矩阵?我们还要利用一个LSZ约化规则,它联系了量子场论中的格林函数和可观测的散射矩阵。这使得理论能够预言实验。
协方差矩阵
在统计学与概率论中,协方差矩阵(或称共变异矩阵)是一个矩阵,其每个元素是各个向量元素之间的方差。这是从标量随机变量到高维度随机向量的自然推广。
假设X是以n个标量随机变量组成的列向量,
并且μi 是其第i个元素的期望值, 即, μi = E(Xi)。协方差矩阵被定义的第i,j项是如下协方差:
即:
矩阵中的第(i,j)个元素是Xi与Xj的协方差。这个概念是对于标量随机变量方差的一般化推广。
术语与符号分歧
协方差矩阵有不同的术语。有些统计学家,沿用了概率学家威廉·费勒的说法,把这个矩阵称之为随机向量X的方差(Variance of random vector X),这是从一维随机变量方差到高维随机向量的自然推广。另外一些则把它称为协方差矩阵(Covariance matrix),因为它是随机向量里头每个标量元素的协方差的矩阵。不幸的是,这两种术语带来了一定程度上的冲突:
随机向量X的方差(Variance of random vector X)定义有如下两种形式:
协方差矩阵(Covariance matrix)定义如下:
第一个记号可以在威廉·费勒的广受推崇的两册概率论及其应用的书中找到。两个术语除了记法之外并没有不同。
性质
![Sigma=mathrm{E} left[ left( textbf{X} - mathrm{E}[textbf{X}] right) left( textbf{X} - mathrm{E}[textbf{X}] right)^top right]](http://upload.wikimedia.org/math/1/8/1/1811f942680a72974597be42c28d31d2.png) 与
与 满足下边的基本性质:
满足下边的基本性质:

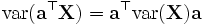




- 若 p = q,则有

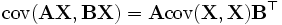
- 若
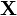 与
与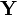 是独立的,则有
是独立的,则有

其中  与
与 是随机
是随机 向量,
向量, 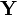 是随机
是随机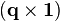 向量,
向量,  是
是 向量,
向量,  与
与 是
是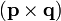 矩阵。
矩阵。
尽管协方差矩阵很简单,可它却是很多领域里的非常有力的工具。它能导出一个变换矩阵,这个矩阵能使数据完全去相关(decorrelation)。从不同的角度看,也就是说能够找出一组最佳的基以紧凑的方式来表达数据。(完整的证明请参考瑞利商)。 这个方法在统计学中被称为主成分分析(principal components analysis),在图像处理中称为Karhunen-Loève 变换(KL-变换)。
复随机向量
均值为μ的复随机标量变量的方差定义如下(使用共轭复数):
其中复数z的共轭记为z * 。
如果Z 是一个复列向量,则取其共轭转置,得到一个方阵:
其中Z * 为共轭转置, 它对于标量也成立,因为标量的转置还是标量。
估计
多元正态分布的协方差矩阵的估计的推导非常精致. 它需要用到谱定义以及为什么把标量看做 矩阵的trace更好的原因。参见协方差矩阵的估计。
矩阵的trace更好的原因。参见协方差矩阵的估计。
| Covariance Matrix | |
Given ![]() sets of variates denoted
sets of variates denoted ![]() , ...,
, ..., ![]() , the first-order covariance matrix is defined by
, the first-order covariance matrix is defined by
where ![]() is the mean. Higher order matrices are given by
is the mean. Higher order matrices are given by
An individual matrix element ![]() is called the covariance of
is called the covariance of ![]() and
and ![]() .
.







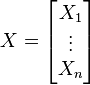

![散射矩阵、协方差矩阵 - 开心五味瓶 - 开心五味瓶的博客 = begin{bmatrix} mathrm{E}[(X_1 - mu_1)(X_1 - mu_1)] & mathrm{E}[(X_1 - mu_1)(X_2 - mu_2)] & cdots & mathrm{E}[(X_1 - mu_1)(X_n - mu_n)] mathrm{E}[(X_2 - mu_2)(X_1 - mu_1)] & mathrm{E}[(X_2 - mu_2)(X_2 - mu_2)] & cdots & mathrm{E}[(X_2 - mu_2)(X_n - mu_n)] vdots & vdots & ddots & vdots mathrm{E}[(X_n - mu_n)(X_1 - mu_1)] & mathrm{E}[(X_n - mu_n)(X_2 - mu_2)] & cdots & mathrm{E}[(X_n - mu_n)(X_n - mu_n)] end{bmatrix}](http://upload.wikimedia.org/math/a/1/2/a12a573ecd1d853abd8c01fab9fccfbe.png)
![operatorname{var}(textbf{X}) = mathrm{E} left[ (textbf{X} - mathrm{E} [textbf{X}]) (textbf{X} - mathrm{E} [textbf{X}])^top right]](http://upload.wikimedia.org/math/2/0/8/20858634ce728c44b89ad3cba1fac25e.png)
![operatorname{cov}(textbf{X}) = mathrm{E} left[ (textbf{X} - mathrm{E}[textbf{X}]) (textbf{X} - mathrm{E}[textbf{X}])^top right]](http://upload.wikimedia.org/math/9/4/3/943a5cd42f6b5b68528e61c02c7a4739.png)
![operatorname{cov}(textbf{X},textbf{Y}) = mathrm{E} left[ (textbf{X} - mathrm{E}[textbf{X}]) (textbf{Y} - mathrm{E}[textbf{Y}])^top right]](http://upload.wikimedia.org/math/e/2/e/e2eb53bc43fed1d17ab4d2431229b266.png)
![operatorname{var}(z) = operatorname{E} left[ (z-mu)(z-mu)^{*} right]](http://upload.wikimedia.org/math/4/d/b/4db5552832ee20b19f0ef057887f2162.png)
![operatorname{E} left[ (Z-mu)(Z-mu)^{*} right]](http://upload.wikimedia.org/math/f/e/6/fe608f7ac94446dffb6af34289617255.png)
















 3257
3257

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








