基于随机游走的图像分割算法
原文地址:http://blog.csdn.net/hjimce/article/details/45201263
作者:hjimce
基于随机游走的图像分割算法是属于图论分割方法中的一种,这个算法比较偏,网上的paper比较少,刚开始学习找个资料都不容易,其实这个算法的原理就是通过求解一个邻接矩阵方程组,跟三维空间三角网格曲面的调和场求解有点类似。
1、算法开始前,先简单描述一下随机游走模型
一维随机游走问题:设一个质点(随机游走者)沿着一条直线运动,单位时间内只能运动一个单位长度,且只能停留在该直线上的整数点,假设在时刻t,该质点位于直线上的点i,那么在时刻t +1,该质点的位置有三种可能:①以p 的概率跳到整数点i-1,②或以q的概率跳到点i+1,③或以r=1-p-q的概率继续停留在点i ,由于每一步的结果都是独立的,且每种情况发生的概率之和都为1,则该过程服从伯努利分布,称为贝努利随机游走过程。当 p=q=0.5时,即质点在下一时刻到达其相邻点的概率是相等的,称为简单的随机游走。
例子1:如下图所示,假设某一时刻一质点位于刻度2的位置,质点左右游走的概率各为0.5,那么下一时刻该质点既有可能往左走,也有可能往右走,当质点运动到位置0、5位置时,质点停止运动,求质点到最后运动到位置5的概率?该问题便是随机游走问题。
对于一维的简单随机游走问题,满足:
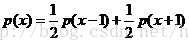
,
其中,x为当前的位置点,x-1、x+1为位置x的左右邻接顶点。根据该公式,我们可以列出由n个未知数组成的n个方程组,可以发现该方程组的系数矩阵即为拉普拉斯邻接矩阵。拉普拉斯矩阵是非满秩矩阵,需要添加边界约束条件,方程组才有唯一解。
如例子1的问题,设添加边界约束条件:
则最后可以列出如下方程组,求出各点到位置5的概率。
2、基于随机游走的图像分割算法
①参考文献:《Random Walks for Image Segmentation》
②文献概述:随机游走算法是一种基于图论的分割算法,属于一种交互式的图像分割。它的分割思想是,以图像的像素为图的顶点,相邻像素之间的四邻域或八邻域关系为图的边,并根据像素属性及相邻像素之间特征的相似性定义图中各边的权值,以此构建网络图,然后由通过用户手工指定前景和背景标记,即前景物体和背景物体的种子像素,以边上的权重为转移概率,未标记像素节点为初始点,计算每个未标记节点首次到达各种子像素的概率,根据概率大小,划分未标记节点,得到最终分割结果。
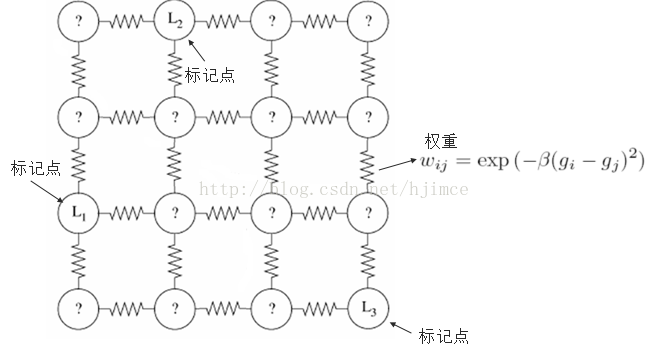
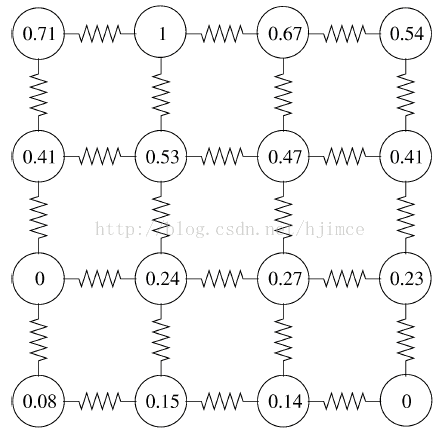
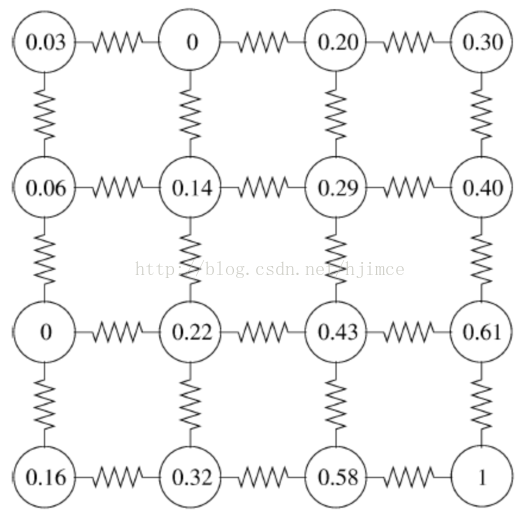
例子2:如图下所示,图中的小圆圈代表图像上的每个像素点。L1,L2,L3三个种子点分别由用户交互输入,作为标记的种子点。现要把图像分割成对应的三部分。
③算法流程:
A.计算图中任意一点vi与其各个邻接顶点连接边的权重:
其中,表示个像素点的灰度值、或纹理信息等参数;
B.对于图中任意一点vi的概率,其满足随机游走概率公式:
其中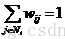
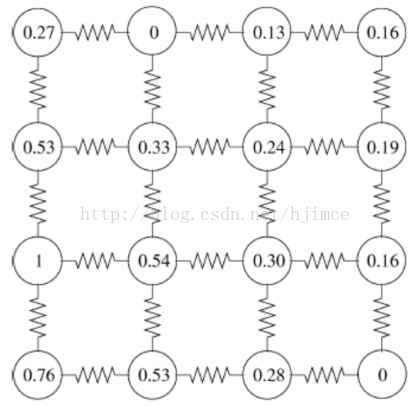
C.添加边界约束条件:以已标记的K类顶点作为边界约束条件,求解未知点到各个类的概率。如下图所示:求解各未知点游走到L1的概率,则以
到达L1的概率
到达L2的概率
到达L3的概率
(5) 每一个未标记点,根据获得的对 K 类标记的隶属度值进行判断,若未标记点到达第k类的概率最大,则将未标记节点vi判别为属于类别k,完成分割。
最后贴一下自己写的部分重要函数代码:
//根据邻接关系,构造拉普拉斯矩阵
void CRandomWalk::ComputeCoff()
{
int height=m_image->Height;
int width=m_image->Width;
m_A.resize(height*width,width*height);
int vn=height*width;
typedef Eigen::Triplet<double> Tri;
std::vector<Tri> tripletList;
for (int i=0;i<height;i++)
{
for (int j=0;j<width;j++)
{
int idex=i*width+j;
Eigen::Vector2i nei[4]={Eigen::Vector2i(i-1,j),Eigen::Vector2i(i,j-1),Eigen::Vector2i(i+1,j),Eigen::Vector2i(i,j+1)};
BYTE *data=GetpData(Eigen::Vector2i(i,j),m_image);
float sumw=0;
for (int k=0;k<4;k++)
{
if (nei[k][0]>=0&&nei[k][0]<height&&nei[k][1]>=0&&nei[k][1]<width)
{
int idexnei=nei[k][0]*width+nei[k][1];
BYTE *neidata=GetpData(nei[k],m_image);
float w=-GetGrad(data,neidata);
w=exp(w/(2*50*50));
sumw+=w;
tripletList.push_back(Tri(idex,idexnei,w));
}
}
//计算A
tripletList.push_back(Tri(idex,idex,-sumw));
}
}
m_A.setFromTriplets(tripletList.begin(),tripletList.end());
m_B.resize(height*width);
m_B.setZero();
}
void CRandomWalk::AddConstrain()
{
for (int i=0;i<m_front.size();i++)
{
int indexf=m_image->Width*m_front[i].y+m_front[i].x;
float a=m_A.coeff(indexf,indexf) +1;
m_A.coeffRef(indexf,indexf)=a;
}
for (int j=0;j<m_back.size();j++)
{
int indexb=m_image->Width*m_back[j].y+m_back[j].x;
float b=m_A.coeff(indexb,indexb) +1;
m_A.coeffRef(indexb,indexb)=b;
}
m_MatricesCholesky=new Eigen::SparseLU<Eigen::SparseMatrix<double>>(m_A);
}
void CRandomWalk::Solver()
{
ComputeCoff();
AddConstrain();
Eigen::VectorXd b=m_B;
for (int i=0;i<m_front.size();i++)
{
int indexf=m_image->Width*m_front[i].y+m_front[i].x;
b(indexf)+=1;
}
Eigen::VectorXd x=m_MatricesCholesky->solve(b);
Eigen::VectorXd bb=m_B;
for (int j=0;j<m_back.size();j++)
{
int indexfb=m_image->Width*m_back[j].y+m_back[j].x;
bb(indexfb)+=1;
}
Eigen::VectorXd y=m_MatricesCholesky->solve(bb);
//比较概率大小
for (int i=0;i<m_image->Height*m_image->Width;i++)
{
if (x(i)>y(i))
{
BYTE *data=(BYTE*)m_image->Scan0+i*4;
for (int k=0;k<3;k++)
{
data[k]=255;
}
}
}
//int indexb=m_image->Width*m_front.y+m_front.x;
}
BYTE* CRandomWalk::GetpData(Eigen::Vector2i pt,BitmapData*image)
{
return (BYTE*)image->Scan0+image->Width*4*pt[0]+4*pt[1];
}
float CRandomWalk::GetGrad(BYTE*data1,BYTE*data2)
{
float sum0=0;
for (int i=0;i<3;i++)
{
sum0+=(data1[i]-data2[i])*(data1[i]-data2[i]);
}
return sum0;
}作者:hjimce 联系qq:1393852684 更多资源请关注我的博客:http://blog.csdn.net/hjimce 原创文章,版权所有,转载请注明出处 。









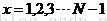

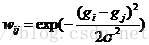
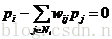














 1019
1019

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








