高等数学学习笔记——第七十讲——方向导数与梯度

 

1. 问题的引入——天气预报中的卫星云图、局部地区等压线等

 

2. 如何刻画二元函数沿不同方向的变化？（方向导数）函数沿什么方向变化最快？（梯度方向）

 

3. 二元函数的偏导数反映了函数沿平行于坐标轴方向的变化率（注：下图中的偏导数应该是标反了）

 

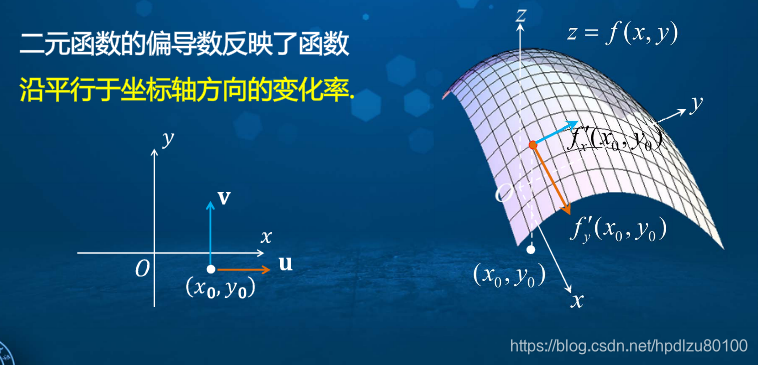
4. 函数在一段有向距离上的平均变化率

 

5. 方向导数的定义（方向导数反映了函数在某点上沿某个方向的变化率；方向导数的正负号表示函数的增减性，方向导数的大小表示变化的快慢）

 

6. 方向导数是偏导数的推广

 

7. 方向导数的几何意义（函数切线与给定方向的夹角的正切值）

 

8. 方向导数的计算方法

 

9. 梯度向量（梯度）的定义

 

10. 方向导数与梯度的关系：方向导数是梯度在给定方向上的投影；梯度方向是函数增加最快的方向；负梯度方向是函数减小最快的方向；与梯度正交的方向函数变化率等于零

 

11. 梯度的几何意义：函数在一点的梯度垂直与通过该点的等值线，指向函数增大的方向

 

12. 梯度的应用非常广泛：河流的流向、行进路线的选择、丘壑的形成、风向的确定等