线性代数学习笔记——第四讲——矩阵乘法的定义

 

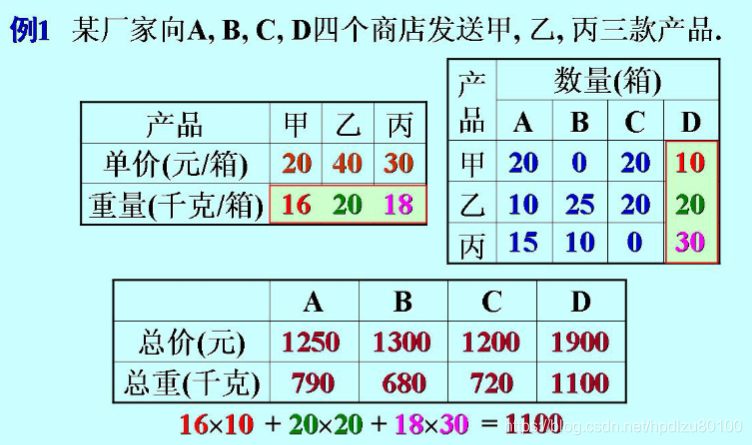
1. 矩阵乘法的应用示例

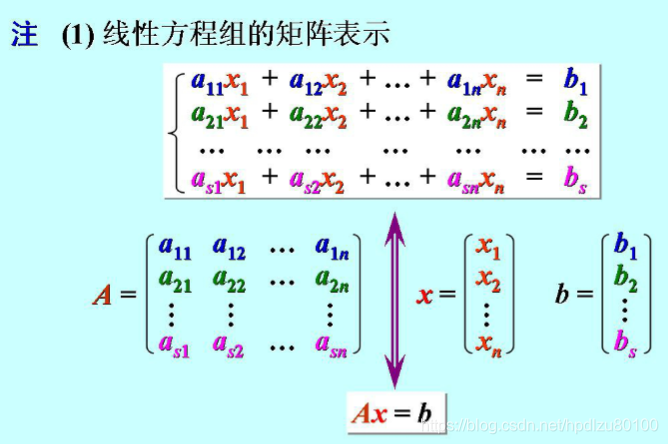
2. 线性方程组可用矩阵表示

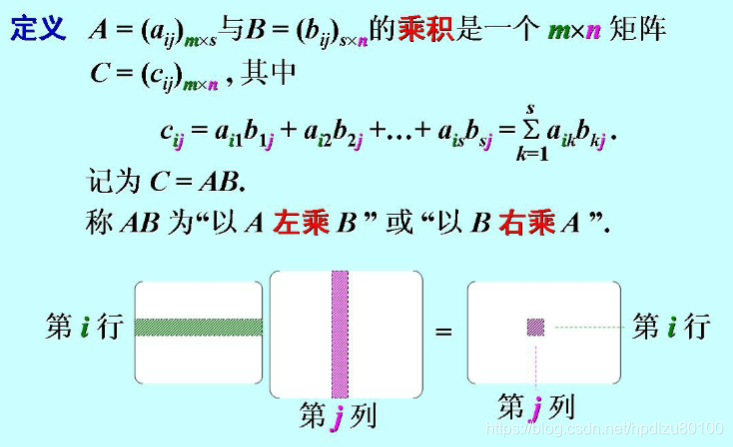
3. 矩阵乘法的定义（自己的表述：积的元素=左行右列元素依次相乘再相加）

4. 矩阵的乘积为零矩阵，并不能说明至少有一个因子等于零矩阵；

 

 

 

矩阵乘法一般不满足消去律（AB=AC，A不等于零矩阵，不能说明B一定等于C），举反例如下：

A			B				AB
1	1		1	2			4	6
2	2		3	4			8	12
A			C				AC
1	1		3	2			4	6
2	2		1	4			8	12
AB = AC, A≠O  ≠> B = C

5. 矩阵乘法一般不满足交换律

6. 同阶对角阵相乘，满足交换律

 7. 单位矩阵左乘右乘一个矩阵，结果还是该矩阵

8. 矩阵乘法和数乘完全不是一个概念

 9. 数的乘法可推广到矩阵乘法（数的乘法是矩阵乘法的一种特例：可看成两个1阶方阵的乘积）。