VAE与CVAE

1. VAE的本质

1.1 深度理解VAE

1. VAE本质就是在我们常规的自编码器的基础上，对encoder的结果（在VAE中对应着计算均值的网络）加上了$“高斯噪声”$，$使得结果decoder能够对噪声有鲁棒性$；而那个额外的KL loss（目的是让均值为0，方差为1），事实上就是相当于对encoder的一个正则项，希望encoder出来的东西均有零均值。

   

2. VAE 中的encoder（对应着计算方差的网络）的作用：是用来$动态调节噪声的强度$的。

   • 当decoder还没有训练好时（$重构误差$远大于KL loss），就会适当$降低噪声$（KL loss增加），使得拟合起来容易一些（重构误差开始下降）；
   • 如果decoder训练得还不错时（$重构误差$小于KL loss），这时$噪声就会增加$（KL loss减少），使得拟合更加困难了（重构误差又开始增加），这时候decoder就要想办法提高它的生成能力了。

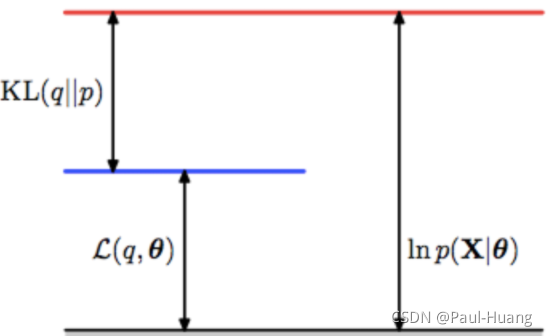
   具体理解参照：下图，以及以下公式

   1. 观测数据集$X={\left\{{\mathtt{x}}^{(i)}\right\}}_{i=1}^{N}i.i.d$（$X$本身可能是连续分布或者离散分布），对某个$x$的概率处理：
      $$\begin{array}{rl}\log p_{\theta }({\mathtt{x}}^{(i)})& =\log p_{\theta }({\mathtt{x}}^{(i)},\mathtt{z})-\log p_{\theta }(\mathtt{z}|{\mathtt{x}}^{(i)})\\ & =\log \frac{p_{\theta }({\mathtt{x}}^{(i)},\mathtt{z})}{q_{\varphi }(\mathtt{z}|{\mathtt{x}}^{(i)})}-\log \frac{p_{\theta }(\mathtt{z}|{\mathtt{x}}^{(i)})}{q_{\varphi }(\mathtt{z}|{\mathtt{x}}^{(i)})}(q_{\varphi }(\mathtt{z}|{\mathtt{x}}^{(i)})\ne 0).\end{array}\text{\hspace{1em}(1.1)}$$
      (2.2.2)式两边对$q_{\varphi }(\mathtt{z}|{\mathtt{x}}^{(i)})$求期望得：
      $$\log p_{\theta }({\mathtt{x}}^{(i)})=D_{KL}(q_{\varphi }(\mathtt{z}|{\mathtt{x}}^{(i)})||p_{\theta }(\mathtt{z}|{\mathtt{x}}^{(i)}))+\mathcal{L}(\theta ,\varphi ;{\mathtt{x}}^{(i)})\text{\hspace{1em}(1.2)}$$
      其中：
      { L ( θ , ϕ ; x ( i ) ) = ∫ z q ϕ ( z ∣ x ( i ) ) log ⁡   p θ ( z , x ( i ) ) q ϕ ( z ∣ x ( i ) ) d z D K L ( q ϕ ( z ∣ x ( i ) ) ∣ ∣ p θ ( z ∣ x ( i ) ) ) = − ∫ z q ϕ ( z ∣ x ( i ) ) log ⁡   p θ ( z ∣ x ( i ) ) q ϕ ( z ∣ x ( i ) ) d z \color{blue}\{ \begin{aligned} \mathcal{L}(\theta,\phi;\mathtt{x}^{(i)})&=\int_z q_{\phi}(\mathtt{z}|\mathtt{x}^{(i)}) \log\ \frac{p_{\theta }(\mathtt{z},\mathtt{x}^{(i)})}{q_{\phi}(\mathtt{z}|\mathtt{x}^{(i)})}dz\\ D_{KL}{(q_{\phi}(\mathtt{z}|\mathtt{x}^{(i)})||p_{\theta }(\mathtt{z}|\mathtt{x}^{(i)}))}&= - \int_z q_{\phi}(\mathtt{z}|\mathtt{x}^{(i)})\log\ \frac{p_{\theta }(\mathtt{z}|\mathtt{x}^{(i)})}{q_{\phi}(\mathtt{z}|\mathtt{x}^{(i)})}dz \end{aligned} {L(θ,ϕ;x(i))DKL​(qϕ​(z∣x(i))∣∣pθ​(z∣x(i)))​=∫z​qϕ​(z∣x(i))log qϕ​(z∣x(i))pθ​(z,x(i))​dz=−∫z​qϕ​(z∣x(i))log qϕ​(z∣x(i))pθ​(z∣x(i))​dz​
      

   2. $\mathcal{L}(\theta ,\varphi ;{\mathtt{x}}^{(i)})$又可以写成：
      $$\begin{array}{rl}& {\tilde{\mathcal{L}}}^B\left(\mathbf{\theta },\mathbf{\varphi };{\mathbf{x}}^{(i)}\right)\simeq \underset{RegularizationLoss}{\underbrace{\frac{1}{2}\sum _{j=1}^J\left(1+\log \left({\left({\sigma }_j^{(i)}\right)}^2\right)-{\left({\mu }_j^{(i)}\right)}^2-{\left({\sigma }_j^{(i)}\right)}^2\right)}}+\underset{ReconstructionLoss}{\underbrace{\frac{1}{L}\sum _{l=1}^L\left(\log p_{\mathbf{\theta }}\left({\mathbf{x}}^{(i)}\mid {\mathbf{z}}^{(i,l)}\right)\right)}}\\ & where{\mathbf{z}}^{(i,l)}=g_{\varphi }({\mathbf{x}}^{(i)},{ϵ}^{(l)})={\mathbf{\mu }}^{(i)}+{\mathbf{\sigma }}^{(\mathbf{i})}\odot {ϵ}^{(l)}and{\mathbf{ϵ}}^{(l)}\sim \mathcal{N}(0,\mathbf{I})\end{array}\text{\hspace{1em}(1.3)}$$

      具体符号意义见：【论文阅读】生成模型——变分自编码器(Variational Auto-Encoder，VAE)公式（3.1.6）

1.2 VAE 与GAN

1. VAE的对抗性
   VAE中$重构的过程是希望没噪声的$，而$KLloss则希望有高斯噪声的$，$两者是对立的$。所以，VAE跟GAN一样，内部其实是包含了一个对抗的过程，只不过它们两者是混合起来，共同进化的。
2. VAE与GAN
   1. VAE是共同进化
   2. GAN的特点
      • $GAN中，造假者在进化时，鉴别者是安然不动的，反之亦然。$
      • GAN真正高明的地方是：$连度量都直接训练出来了，而且这个度量往往比人工想的要好。$
3. VAE的准确性
   每个$p(Z|X)$是不可能完全精确等于标准正态分布，否则$p(Z|X)$就相当于跟$X$无关了，重构效果将会极差。最终的结果就会是，$p(Z|X)$保留了一定的$X$信息，重构效果也还可以，并且下式近似成立，所以同时保留着生成能力。
   $$p(Z)=\sum _{X}p(Z\mid X)p(X)=\sum _X\mathcal{N}(0,I)p(X)=\mathcal{N}(0,I)\sum _{X}p(X)=\mathcal{N}(0,I)\text{\hspace{1em}(1.4)}$$

---

2. CVAE

2.1 CVAE简介

1. VAE是无监督训练的，因此很自然想到：如果有标签数据，那么能不能把标签信息加进去辅助生成样本呢？这个问题的意图，往往是希望能够实现控制某个变量来实现生成某一类图像。当然，这是肯定可以的，我们把这种情况叫做Conditional VAE，或者叫CVAE。（相应地，在GAN中我们也有个CGAN。）

2. 但是，$CVAE不是一个特定的模型，而是一类模型$，总之就是$把标签信息融入到VAE中的方式有很多，目的也不一样$。这里基于前面的讨论，给出一种非常简单的VAE。

2.2 CVAE基本模型

1. VAE与CVAE对比
   • VAE基本模型：
     
   • CVAE基本模型：
     

2.3 数学理解

• VAE中希望$X$经过编码后，$Z$的分布都具有零均值和单位方差，这个“希望”是通过加入了KL loss来实现的。如果现在多了类别信息$Y$。
• CVAE希望同一个类的样本都有一个专属的均值${\mu }^Y$（方差不变，还是单位方差），这个${\mu }^Y$让模型自己训练出来。这样的话，有多少个类就有多少个正态分布，而在生成的时候，我们就可以通过控制均值来控制生成图像的类别。
• 事实上，这样可能也是在VAE的基础上加入最少的代码来实现CVAE的方案了，因为这个“新希望”也只需通过修改KL loss实现：
  $$\begin{array}{rl}& {\tilde{\mathcal{L}}}^B\left(\mathbf{\theta },\mathbf{\varphi };{\mathbf{x}}^{(i)}\right)\simeq \underset{RegularizationLoss}{\underbrace{\frac{1}{2}\sum _{j=1}^J\left(1+\log \left({\left({\sigma }_j^{(i)}\right)}^2\right)-{\left({\mu }_j^{(i)}-{\mu }_j^{Y^{(i)}}\right)}^2-{\left({\sigma }_j^{(i)}\right)}^2\right)}}+\underset{ReconstructionLoss}{\underbrace{\frac{1}{L}\sum _{l=1}^L\left(\log p_{\mathbf{\theta }}\left({\mathbf{x}}^{(i)}\mid {\mathbf{z}}^{(i,l)}\right)\right)}}\\ & where{\mathbf{z}}^{(i,l)}=g_{\varphi }({\mathbf{x}}^{(i)},{ϵ}^{(l)})={\mathbf{\mu }}^{(i)}+{\mathbf{\sigma }}^{(\mathbf{i})}\odot {ϵ}^{(l)}and{\mathbf{ϵ}}^{(l)}\sim \mathcal{N}(0,\mathbf{I})\end{array}\text{\hspace{1em}(2.1)}$$

更多内容，参考：CVAE

参考

1. 变分自编码器（一）：原来是这么一回事
2. 代码