阅读论文：稀疏阵列波达方向估计

最新推荐文章于 2024-07-20 09:51:47 发布

Coder~Sheep

最新推荐文章于 2024-07-20 09:51:47 发布

阅读量1k

点赞数 15

文章标签：算法信号处理 matlab 机器学习信息可视化

本文链接：https://blog.csdn.net/huangdaxian0/article/details/137522103

版权

摘要

此传统的阵列结构阵元间距设计一般不大于半波长。而波达方向估计的分辨率通常受到阵列孔径的影响。

在实际的复杂电磁环境下，往往会有信号源数大于阵元数的情况，即欠定问题。

对 MUSIC 算法无法直接应用到稀疏阵列中的问题，介绍了基于协方差矩阵向量化的 MUSIC 改进算法，首先对接收到的阵列协方差矩阵进行向量化排序，以重构采样协方差矩阵，从而增大虚拟阵列的孔径，之后利用空间平滑算法进行秩恢复，最后使用 MUSIC 算法对DOA 进行估计。

1 绪论

1.1 课题背景及研究的目的和意义

阵列是根据实际需求将多个传感器按照一定的规则在空间排布组成的系统。

子空间算法实现了超分辨，分辨率相比波束形成算法大大提高，但只能应用于信号和噪声相互独立的场景。

由空间谱理论知识可知，空间阵列接收信号要求阵列相邻阵元间距不大于信号半波长，否则信号估计时会不可避免地出现角度模糊的问题。但是阵元间距太近又会造成阵元间的耦合等一系列影响，造成估计精度下降，而且由于间距受限，会导致阵列孔径变小，分辨率下降。而且在目前复杂的空间电磁信号背景下，信号辐射源较多，传统均匀阵列只能处理的信号源数需要小于阵元数，无法满足实际需求。

相比于均匀阵列，稀疏阵列的设计思想具有如下优势：(1) 阵元间距可以大于半波长，布阵更加灵活，而且可以减小阵元间的耦合，减弱耦合造成的影响。(2) 相同的阵列孔径，可以减少阵元数，从而降低成本。(3) 在阵元数相同的情况下，稀疏阵列由于阵元间距变大，可以获得更好的角度分辨性能。而且通过一定的算法可以提高阵列的自由度，从而同时可以处理的信号源数增加，适用于更加复杂的场景。

1.2 国内外研究现状及分析

1.2.2 稀疏阵列DOA估计算法研究现状

相比于均匀阵列，稀疏阵列存在的主要问题是由于阵元间距过大造成的角度模糊，而传统 DOA 估计算法通常不考虑角度模糊的问题，因此不适用于稀疏阵列。针对稀疏阵列，主要可分为子阵分解和虚拟阵列信号处理等两大类算法。

互质阵列，将 MUCIC 算法分别应用到互质阵列的两个子阵中进行谱估计，利用互质的条件解相位模糊从而得到 DOA 估计。该算法计算简单，但是由于两个子阵分开计算，其分辨率不超过两子阵各自的分辨率，而且阵列自由度下降。

子阵分解思想简单且易于计算，但是只能用于互质阵列，对于其他类型稀疏阵列并不适用。虚拟阵列的思想是稀疏阵列的协方差矩阵具有较多信息，通过将信息充分利用从而形成大孔径虚拟阵列，提高分辨率和估计性能。

稀疏阵列的虚拟阵列会有孔的存在，因此，部分研究者又从这方面开展研究，探寻填补孔信息的算法。

2 稀疏阵列DOA估计理论基础

2.1 阵列信号模型

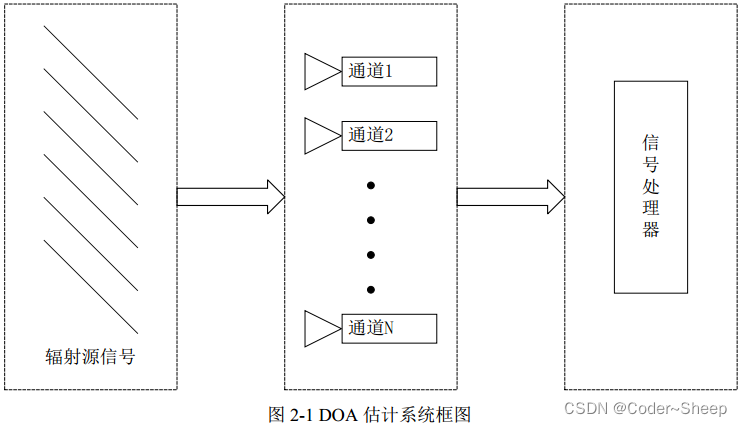
为了简化信号模型，做出如下假设：
(1) 接收信号符合远场窄带模型，且各信号源不相关；
(2) 信号噪声为零均值高斯噪声；
(3) 各阵元间互耦以及阵元位置偏差等因素不予考虑。
假设有 K 个不相关辐射源信号入射到空间接收阵列中，接收阵列采用一维均匀阵列，处理器用以处理来自 N 个阵元的接收数据。窄带信号模型满足：
$\begin{cases}s_i(t)=u_i(t)\mathrm{e}^{j(\omega_0t+\varphi(t))}\\s_i(t-\tau)=u_i(t-\tau)\mathrm{e}^{j(\omega_0(t-\tau)+\varphi(t-\tau))}\end{cases}\text{(2-1)}$

ui(t) ，ω0 ，ϕ(t)t分别表示接收信号的幅度、频率和相位，τ表示接收信号的时延 $\begin{cases}u_i(t-\tau)\approx u_i(t)\\\varphi(t-\tau)\approx\varphi(t)\end{cases}$

$s_i(t-\tau)\approx s_i(t)\mathrm{e}^{-j\omega_0\tau}\quad i=1,2,\cdots,K$

第m 个阵元接收到的信号为：

2.2 稀疏阵列基本概念

2.2.1 差分集合

假设阵列共有 N 个阵元，阵列集合设为， m d 代表阵列第m 个阵元的相对于参考阵元的位置，定义差分集合为：
$D=\{d_{m}-d_{n},\forall d_{m},d_{n}\in\mathbb{S}\}$
D 为一个集合，由不同阵元的位置差组成。集合 D 中元素的个数决定了接收阵列
虚拟孔径的大小。通过修改阵列的布阵形式，可以使得在相同阵元数的情况下，集
合 D 的元素个数增加，从而增大阵列孔径大小。

$x_m(t)=\sum_{i=1}^N\omega_{mi}s_i\left(t-\tau_{mi}\right)+n_m(t)\quad m=1,2,\cdots,N$

nm（t)表示接收噪声，ωmi表示方向图增益 $\begin{bmatrix}x_1(t)\\x_2(t)\\\vdots\\x_N(t)\end{bmatrix}=\begin{bmatrix}\omega_{11}\mathrm{e}^{-j\omega_0\tau_{11}}&\omega_{12}\mathrm{e}^{-j\omega_0\tau_{12}}&\cdots&\omega_{1K}\mathrm{e}^{-j\omega_0\tau_{1K}}\\\omega_{21}\mathrm{e}^{-j\omega_0\tau_{21}}&\omega_{22}\mathrm{e}^{-j\omega_0\tau_{22}}&\cdots&\omega_{2K}\mathrm{e}^{-j\omega_0\tau_{2K}}\\\vdots&\vdots&\vdots\\\omega_{N1}\mathrm{e}^{-j\omega_0\tau_{N1}}&\omega_{N2}\mathrm{e}^{-j\omega_0\tau_{N2}}&\cdots&\omega_{NK}\mathrm{e}^{-j\omega_0\tau_{NK}}\end{bmatrix}\begin{bmatrix}s_1(t)\\s_2(t)\\\vdots\\s_K(t)\end{bmatrix}+\begin{bmatrix}n_1(t)\\n_2(t)\\\vdots\\n_K(t)\end{bmatrix}$

$X(t)=\mathbf{A}S(t)+N(t)$

时延τ 的表达式为： $\tau=\frac{d\sin(\theta)}c$ 式中，d 表示阵元间距，θ 表示信号入射方向，c 表示光速。

2.2.2 稀疏阵列信号模型

稀疏阵列的概念是相对于传统均匀阵列提出的，它表示阵列中存在相邻两阵元的间距大于λ / 2，且阵元间距不全部相等。

假设稀疏阵列有 M 个阵元，其阵元位置设为 $S=[d_1,d_2,\cdots,d_M]d$
其中，di通常取为整数，d 设为半波长。依然假设有 K 个辐射源信号被阵列接收，入射角分别为 $\overline{\theta_1,\theta_2,\cdots,\theta_K}$ ，

阵列流型矢量表示为： $\mathbf{a}(\theta_{k})=[e^{-j\omega_{0}\tau_{1}},e^{-j\omega_{0}\tau_{2}},\cdots,e^{-j\omega_{0}\tau_{M}} ]\\\tau_{i}=\frac{d_{i}d\sin(\theta)}{c}$

稀疏阵列接收信号的协方差矩阵可表示为： $\begin{bmatrix}\mathbf{R}_{XX}\end{bmatrix}=E\begin{bmatrix}XX^H\end{bmatrix}$ $=\mathbf{AR}_{s}\mathbf{A}^{H}+\sigma_{n}^{2}\mathbf{I}_{M}$ $=\sum_{i=1}^K\sigma_i^2\mathbf{a}\left(\theta_i\right)\mathbf{a}^H\left(\theta_i\right)+\sigma_n^2\mathbf{I}_M$

接收信号矩阵RXX 的第 m 行 n 列的元素可表示为： $\left[\mathbf{R}_{XX}\right]_{m,n}=\sum_{i=1}^{K}\sigma_{i}^{2}e^{-j2\pi(d_{m}-d_{n})d\sin\theta_{i}/\lambda}+\sigma_{n}^{2}\delta_{m,n}$ $\delta_{m,n}=\begin{cases}1&m=n\\0&m\neq n\end{cases}$

物理阵列的接收数据协方差矩阵中的元素与以差分集合布阵的阵列接收数据协方差矩阵的元素相同，只是两者在矩阵中的位置有所不同。所以，需要对协方差矩阵的元素按照差分集合的顺序进行排列以替换为虚拟阵列，即可得到等效接收数据。对接收数据协方差矩阵 RXX 展开，可以表示为： $z=vec(\mathbf{R}_{xx})=vec(\mathbf{AR}_s\mathbf{A}^H+\boldsymbol{\sigma}_n^2\mathbf{I}_M)$ $=vec\biggl(\sum_{i=1}^K\sigma_i^2\mathbf{a}\bigl(\theta_i\bigr)\mathbf{a}^H\bigl(\theta_i\bigr)+\sigma_n^2\mathbf{I}_M\biggr)$ $=\left(\mathbf{A}^*\odot\mathbf{A}\right)p+\sigma_n^2\vec{\mathbf{I}}_M^2$

vec 表示向量化， $\text{®}$ 表示 Khatri-Rao 积, $\mathbf{A}^*\odot\mathbf{A}$ 表示为： $\mathbf{A}^*\odot\mathbf{A}=\left\lceil\mathbf{a}^*(\theta_1)\otimes\mathbf{a}(\theta_1),\mathbf{a}^*(\theta_2)\otimes\mathbf{a}(\theta_2),\cdots,\mathbf{a}^*(\theta_K)\otimes\mathbf{a}(\theta_K)\right\rceil\in\mathbb{C}^{M^2\times K}$

以将向量化后的数据 z 看成是以虚拟阵列形式布阵的阵列接收到的数据，由于向量化操作，接收模型接收到的数据变为单快拍数据。其中 p 表示单快拍入射信号， $\mathbf{A}^*\odot\mathbf{A}$ 表示等效阵列的流型矢
量。由于只接收到单快拍数据，而协方差矩阵的秩决定了可处理的信号源数，因此无法直接使用该数据的协方差矩阵。
虚拟阵列的阵元数远大于原始物理稀疏阵列的阵元数，稀疏阵列就是基于这一基本原理进行设计的。通过减少物理阵元数，但是保持其虚拟阵列的阵元数不变，从而达到稀疏阵列的形式。

2.3 常用稀疏阵列结构

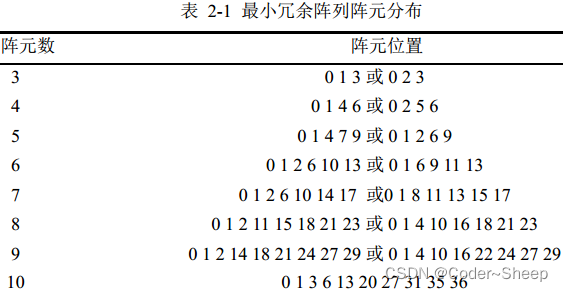
2.3.1 最小冗余阵列

最小冗余阵列的冗余度最低，但是该阵列的设计没有明确的阵元位置表达式，只能通过计算机穷举获得。

2.3.2 嵌套阵列

两级嵌套阵列主要由两组均匀阵列嵌套而成，假设两组均匀阵列阵元间距分别d1 、d2，阵元个数分别为 M1 、 M2 ，则两级均匀阵列的阵元间距满足：d2=(M1+1)d1第二级阵列的第一个阵元与第一级阵列的最后一个阵元的间距也为 d1。第一级阵列像是嵌套在第二级阵列中，形成了嵌套阵列。其差分集合可以表示为：

2.3.3 互质阵列

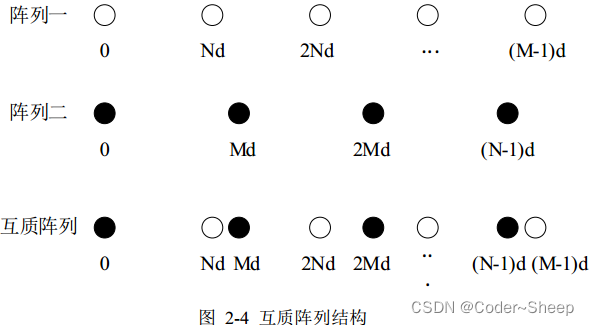
互质阵列是由两组均匀稀疏阵列按照一定规则分布而成，两组阵列阵元数分别为 M 和 N，且 M 和 N 互质，阵元数为 M 的阵列，其阵元间距为 Nd，阵元数为N 的阵列其阵元间距为 Md，d 为单位阵元间距，满足d ≤ λ / 2，λ 为信号波长。两组均匀子阵共享第一个阵元，由于互质的关系，两组阵列的阵元位置交错分布，不发生重合，因此，阵列的阵元数为 M N+ −1。阵元位置表达式为：
$S_{M}=\{mNd,m=0,1,\cdots,M-1\}\\S_{N}=\{nMd,n=0,1,\cdots,N-1\}$

由于互质阵列两组均为稀疏阵列，因此可以有效地降低阵元耦合的影响。互质分布相对于嵌套分布，进一步地增大了阵列自由度，但是带来的问题是其差分集合是不连续的，会有孔的存在，在进行 DOA 估计时会造成部分阵元信息的损失。

2.3.4 改进互质阵列

2.3.4.1 扩展互质阵列

将原来 M 个阵元的阵列个数增加到 2M个，而保持其阵元间距不发生变化

2.3.4.2 压缩内部阵元间距的互质阵列

压缩阵元间距的互质阵列是将阵元间距为 Md 的阵列其间距乘以一个压缩因子 p，即 $\bar{M}=M / p, 2\leq p\leq M$
其虚拟连续阵元位置为： $[-MN+M(N-1)+1,MN-M(N-1)-1]$
相对于互质阵列，增加了连续虚拟阵列的长度，减少了孔的个数。

2.3.4.3 移动子阵的互质阵列

移动子阵的互质阵列（coprime array with displaced subarrays，CADiS）结合了嵌套阵列和 CACIS 的基本思想，将 CACIS 的第二组均匀子阵向右移动一定距离，构成了新的阵列.

2.4 稀疏阵列方向图

w表示阵列的阵元加权，则阵列的方向图可以表示为: $F(\theta)=w^H\mathbf{a}(\theta)$ ,。权重 W 通常设为 1，对方向图做归一化处理可得： $G(\theta)=20\lg\frac{\begin{vmatrix}F(\theta)\end{vmatrix}}{\max(\begin{vmatrix}F(\theta)\end{vmatrix})}$

未完待续

Coder~Sheep

关注

15
点赞
踩
16

收藏

觉得还不错? 一键收藏
0
评论
阅读论文：稀疏阵列波达方向估计

此传统的阵列结构阵元间距设计一般不大于半波长。而波达方向估计的分辨率通常受到阵列孔径的影响。在实际的复杂电磁环境下，往往会有信号源数大于阵元数的情况，即欠定问题。对 MUSIC 算法无法直接应用到稀疏阵列中的问题，介绍了基于协方差矩阵向量化的 MUSIC 改进算法，首先对接收到的阵列协方差矩阵进行向量化排序，以重构采样协方差矩阵，从而增大虚拟阵列的孔径，之后利用空间平滑算法进行秩恢复，最后使用 MUSIC 算法对DOA 进行估计。
复制链接

扫一扫