题解：[USACO06OCT] Cows on Skates G

这道题非常 复杂 简单
洛谷题目

前置的前置

我这篇题解跟洛谷的管理员好好商量都没能把这篇题解交道题解区，我真的心态崩了，所以这篇题解对你有帮助的话，点个赞吧$$\text{o}(╥﹏╥)o求求了$$

另外如果你对这篇题解有任何问题，随时问，24小时解答

前置知识

我借用一下我另一篇题解的讲解（引用于文章）

深度优先搜索（Depth First Search，简称DFS）就是在一棵树一直往自己的子节点搜索，直到再也没有子节点。之后回到父节点，搜另一个字节点。重复直到找到满足题意的节点。

例如：我们要在一棵树上找到苹果（作图略显粗糙）

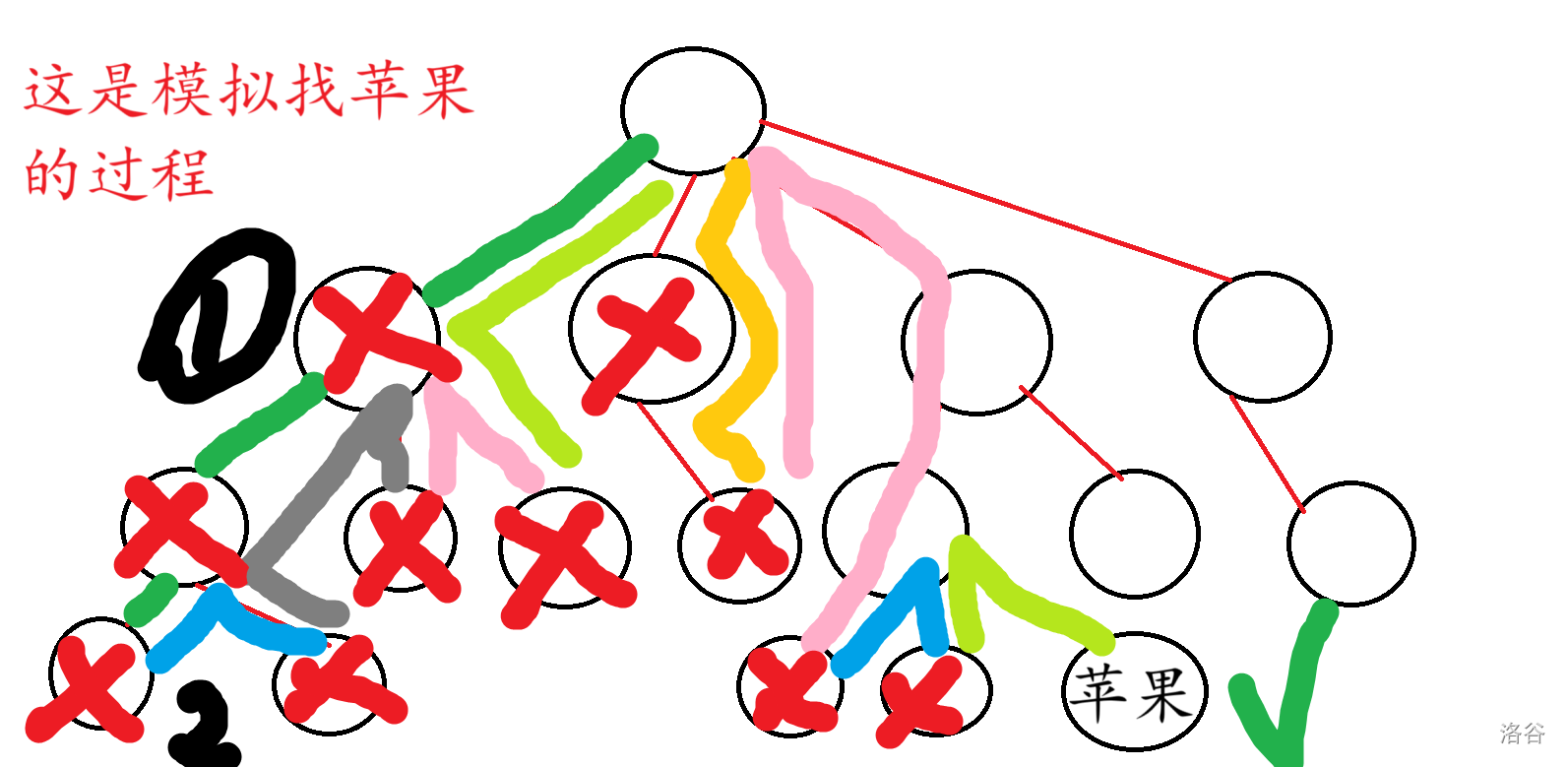
通过模拟，我们能找到苹果

所以根据上图的模拟，我们就得到了DFS框架：

#include<bits/stdc++.h>
using namespace std;
int ans;
const int dx[4]={-1,0,1,0},dy[4]={0,-1,0,1};
bool f[1005][1005];//标记走过路线
bool dfs(int x,int y){
  if(x==n&&y==m)return true;
  int tx,ty;
  for(int i=0;i<=3;i++){
    tx=x+dx[i],ty=y+dy[i];
    if(tx>n||tx<1||ty>m||ty<1||f[tx][ty]==true)continue;
    f[tx][ty]=true;
    ans++
    dfs(tx,ty);
  }
  return false
}
int main(){
  pass();//c++114514新语法代表目前跳过此函数
  return 0;
}

这个代码的时间复杂度太高，于是我们加入一些优化，可以将代码运行效率更高。（即最优步数）

将dfs改成这样,f改成int数组
void dfs(int x,int y,int len){
	if(f[x][y]<len)return;
	f[x][y]=len;
	if(x==n&&y==m){
		ans=min(ans,len);
		return;
	}
	int tx,ty;
	for(int i=0;i<4;i++){
		tx=x+dx[i],ty=y+dy[i];
		if(tx>n||tx<1||ty>m||ty<1&&f[tx][ty]>len+1)dfs(tx,ty,len+1);
	}
}

关于这道题

这道走迷宫的问题没有让你必须走到左下，于是只考虑走就完事了

至于走法，把x,y压进两个**向量**数组就行了（用结构体也行，我没用，你可以试试）

还有一条：回溯算法，百度百科给出这样的定义：回溯法是一种通过搜索所有可能的候选解来找出所有解的算法。‌这种算法通过搜索问题的解空间树来工作，‌采用深度优先策略，‌当一条路径走到尽头时，‌算法会回溯到之前的节点尝试其他可能的路径，‌直到找到所有解或确定没有解为止

代码：

#include<bits/stdc++.h>
using namespace std;
char s[120][100];
int bx,by,n,m;
bool vis[120][100];
vector<int>ansx,ansy;
const int dx[4]={-1,0,1,0};
const int dy[4]={0,-1,0,1};
bool check(int x,int y){
	if(x>=1&&x<=n&&y>=1&&y<=m&&s[x][y]!='*')return true;
	return false;
}
bool dfs(int x,int y){
	if(x==n&&y==m) {
		for(int i=0;i<ansx.size();i++){
			cout<<ansx[i]<<" "<<ansy[i]<<endl;
		}//输出数组
		return true;
	}
	vis[x][y]=true;
	int tx,ty;
	for(int i=0;i<4;i++){
		tx=x+dx[i];ty=y+dy[i];
		if(check(tx,ty)&&(!vis[tx][ty])){
			ansx.push_back(tx);//把坐标压到数组里，下同
			ansy.push_back(ty);
			if(dfs(tx,ty))return true;
			ansx.pop_back();//回溯，意思是刚才的思路行不通，就换一种思路，并把刚才的思路清空，下同
			ansy.pop_back();
		}
		
	}
	return false;
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)scanf("%s",s[i]+1);
	ansx.push_back(1);
	ansy.push_back(1);
	dfs(1,1);
	return 0;
}