从一维卷积、因果卷积(Causal CNN)、扩展卷积(Dilation CNN) 到 时间卷积网络 (TCN)

原文链接：https://blog.csdn.net/yinizhilianlove/article/details/127129520

引言

卷积神经网络 (CNN) 尽管通常与图像分类任务相关，但经过改造，同样可以用于序列建模预测。在本文中，我们将详细探讨时间卷积网络 (TCN) 所包含的基本构建块，以及它们如何组合在一起从而变成强大的预测模型。本文对时间卷积网络 (TCN)的描述基于以下论文：https://arxiv.org/pdf/1803.01271.pdf

关注 AINLPer公众号，最新干货第一时间送达

背景介绍

直到最近，深度学习背景下的序列建模主题在很大程度上与循环神经网络架构有关，例如 LSTM 和 GRU。 S. Bai等人表明这种思维方式已经过时，在对序列数据进行建模时，应将卷积网络作为主要候选者之一。他们证明了卷积网络可以在许多任务中实现比 RNN 更好的性能，同时避免循环模型的常见缺点，例如梯度爆炸/消失问题或缺乏记忆保留。此外，使用卷积网络可以提高性能，因为它允许并行计算输出。他们提出的架构称为时间卷积网络 (TCN)，将在以下部分中进行解释。

卷积模型

 TCN是时域卷积网络的缩写，由具有相同输入和输出长度的扩展(dilated)/因果(causal)一维卷积层组成。下面将详细介绍这些术语的实际含义。

一维卷积网络

 一维卷积网络将一个 3 维张量作为输入，并输出一个 3 维张量。我们的 TCN 实现的输入张量具有形状 (batch_size, input_length, input_size)，输出张量具有形状 (batch_size, input_length, output_size)。由于 TCN 中的每一层都具有相同的输入和输出长度，因此只有输入和输出张量的第三维不同。在单变量情况下，input_size 和 output_size 都将等于 1。在更一般的多变量情况下，input_size 和 output_size 可能不同，因为我们可能不想预测输入序列的每个分量。

 一个单一的 1D 卷积层接收一个形状为 (batch_size, input_length, nr_input_channels) 的输入张量，并输出一个形状为 (batch_size, input_length, nr_output_channels) 的张量。要了解单个层如何将其输入转换为输出，让我们看一下批处理中的一个元素（批处理中的每个元素都发生相同的过程）。让我们从最简单的情况开始，其中 nr_input_channels 和 nr_output_channels 都等于 1。在这种情况下，我们正在查看 1D 输入和输出张量。下图显示了如何计算输出张量的一个元素。

 可以看到，为了计算输出的一个元素，我们查看输入的长度为 kernel_size 的一系列连续元素。 在上面的示例中，我们选择了 kernel_size 为 3。为了获得输出，我们将输入的子序列与相同长度的学习权重的核向量进行点积。 为了获得输出的下一个元素，应用相同的过程，但是输入序列的 kernel_size 大小的窗口向右移动一个元素（对于这个预测模型，步幅始终设置为 1）。这里需要注意，同一组内核权重将用于计算一个卷积层的每个输出。 下图显示了两个连续的输出元素及其各自的输入子序列。

 为了使可视化更简单，不再显示具有核向量的点积，而是针对具有相同核权重的每个输出元素进行。

 为了确保输出序列与输入序列具有相同的长度，应用了一些零填充。这意味着将额外的零值条目添加到输入张量的开头或结尾，以确保输出具有所需的长度。具体如何做到这一点将在后面解释。

 现在让我们看看我们有多个输入通道的情况，即 nr_input_channels 大于 1。在这种情况下，上述过程对每个输入通道重复，但每次使用不同的内核。这将生成 nr_input_channels 中间输出向量和一些 kernel_size * nr_input_channels 的内核权重。然后，将所有的中间输出向量相加得到最终的输出向量。从某种意义上说，这相当于一个二维卷积，其输入张量为 (input_size, nr_input_channels)，内核为 (kernel_size, nr_input_channels)，如下图所示。它仍然是 1D，因为窗口仅沿单个轴移动，但我们在每一步都有一个 2D 卷积，因为我们使用的是 2 维内核矩阵。

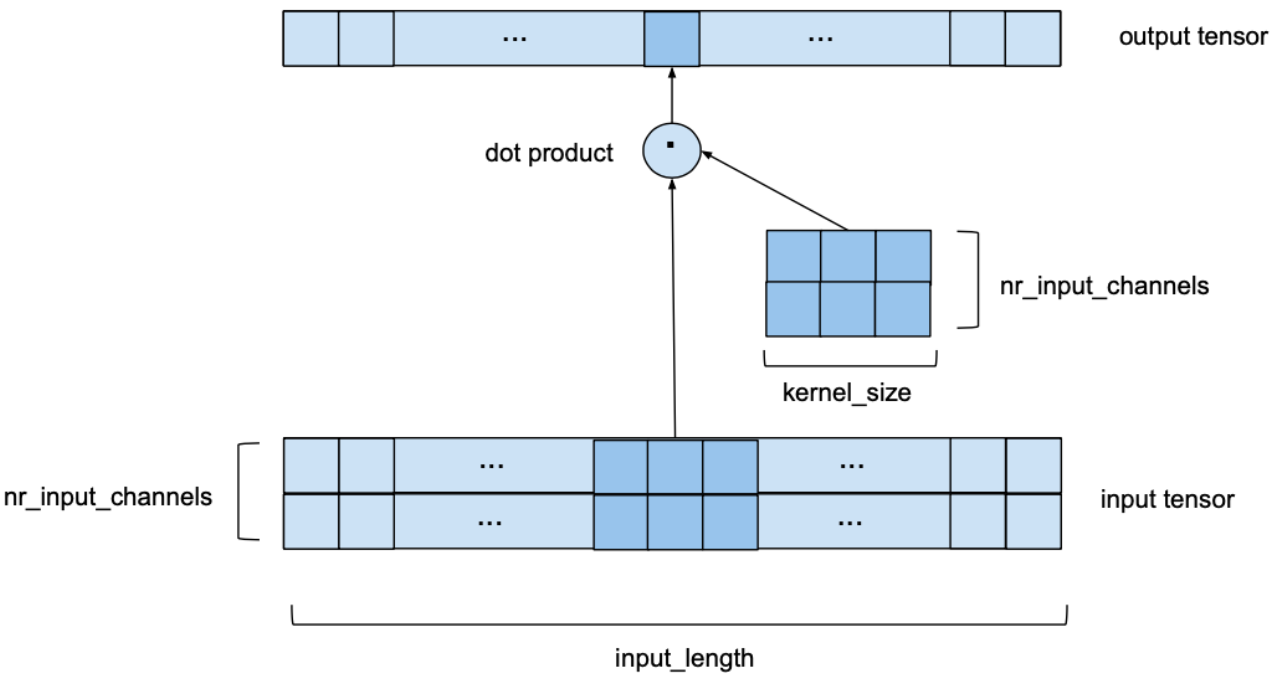
 对于这个例子，我们选择 nr_input_channels 等于 2。现在，我们有一个 nr_input_channels 通过 kernel_size 内核矩阵沿 nr_input_channels 宽系列长度 input_length 滑动，而不是在 1 维输入序列上滑动。

 如果 nr_input_channels 和 nr_output_channels 都大于 1，则只需对具有不同内核矩阵的每个输出通道重复上述过程。 然后将输出向量堆叠在一起，形成形状为 (input_length, nr_output_channels) 的输出张量。 在这种情况下，内核权重的数量等于 kernel_sizenr_input_channelsnr_output_channels。

 两个变量 nr_input_channels 和 nr_output_channels 取决于层在网络中的位置。 第一层的 nr_input_channels = input_size，最后一层的 nr_output_channels = output_size。 所有其他层将使用 num_filters 给出的中间通道号。

因果（Causal ）卷积

 对于因果关系的卷积层，对于

    {
   
   
    0
   
   
    ,
   
   
    .
   
   
    .
   
   
    .
   
   
    ,
   
   
    i
   
   
    n
   
   
    p
   
   
    u
   
   
    t
   
   
    _
   
   
    l
   
   
    e
   
   
    n
   
   
    g
   
   
    t
   
   
    h
   
   
    —
   
   
    1
   
   
    }
   
  
  
   \{0, ..., input\_length— 1\}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.06em; vertical-align: -0.31em;"></span><span class="mopen">{<!-- --></span><span class="mord">0</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mord">...</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mord mathnormal">in</span><span class="mord mathnormal">p</span><span class="mord mathnormal">u</span><span class="mord mathnormal">t</span><span class="mord" style="margin-right: 0.0278em;">_</span><span class="mord mathnormal" style="margin-right: 0.0197em;">l</span><span class="mord mathnormal">e</span><span class="mord mathnormal">n</span><span class="mord mathnormal" style="margin-right: 0.0359em;">g</span><span class="mord mathnormal">t</span><span class="mord mathnormal">h</span><span class="mord">—1</span><span class="mclose">}</span></span></span></span></span> 中的每个i，输出序列的第i个元素可能仅取决于索引为 {0, …, i} 的输入序列的元素。换句话说，输出序列中的一个元素只能依赖于输入序列中它之前的元素。如前所述，为了确保输出张量与输入张量具有相同的长度，我们需要应用零填充。如果我们只在输入张量的左侧应用零填充，那么将确保因果卷积。要理解这一点，请考虑最右边的输出元素。鉴于输入序列的右侧没有填充，它依赖的最后一个元素是输入的最后一个元素。现在考虑输出序列的倒数第二个输出元素。与最后一个输出元素相比，它的内核窗口向左移动了一个，这意味着它在输入序列中最右边的依赖关系是输入序列的倒数第二个元素。通过归纳可知，对于输出序列中的每个元素，其在输入序列中的最新依赖项具有与其自身相同的索引。下图显示了 input_length 为 4 且 kernel_size 为 3 的示例。<br> <img src="https://img-blog.csdnimg.cn/img_convert/1253cc41a8a65f939da6f5e17c57f88c.png" alt=""><br>  我们可以看到，通过 2 个条目的左零填充，我们可以在遵守因果关系规则的同时实现相同的输出长度。 事实上，在没有膨胀的情况下，维持输入长度所需的零填充条目数始终等于 kernel_size – 1。</p> 

扩张（Dilation）卷积

 预测模型的一个理想特性是，输出中特定条目的值依赖于输入中所有之前的条目，即索引小于或等于其本身的所有条目。当接收字段(即影响输出的特定条目的原始输入条目集)的大小为input_length时，就可以实现这一点。我们也称之为“全历史报道”。正如我们前面看到的，一个传统的卷积层使输出中的条目依赖于索引小于或等于其本身的输入的kernel_size条目。例如，如果kernel_size为3，则输出中的第5个元素将依赖于输入的元素3,4和5。当我们把多层叠在一起时，这个范围就会扩大。在下面的图中，我们可以看到通过使用kernel_size 3堆叠两个层，我们得到了一个大小为5的接收字段。

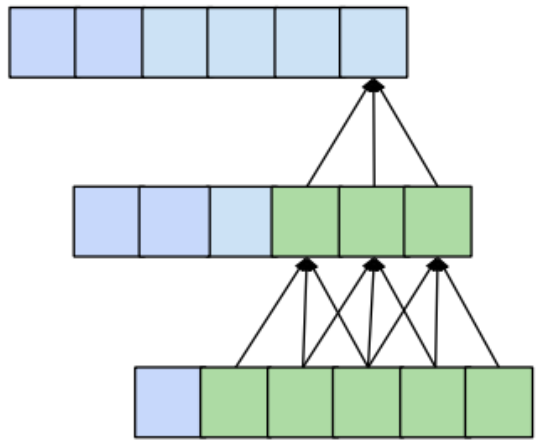
 更一般地，具有 n 层和 kernel_sizek 的一维卷积网络具有大小为r的感受区域。

     r
    
    
     =
    
    
     1
    
    
     +
    
    
     n
    
    
     ∗
    
    
     (
    
    
     k
    
    
     −
    
    
     1
    
    
     )
    
   
   
    r=1+n*(k-1)
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal" style="margin-right: 0.0278em;">r</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.7278em; vertical-align: -0.0833em;"></span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 0.4653em;"></span><span class="mord mathnormal">n</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">∗</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mclose">)</span></span></span></span></span></span><br>  要知道全覆盖需要多少层，我们可以将感受野大小设置为 input_length l 并求解层数 n（如果是非整数值，我们需要四舍五入）：<span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     n
    
    
     =
    
    
     [
    
    
     (
    
    
     l
    
    
     −
    
    
     1
    
    
     )
    
    
     /
    
    
     (
    
    
     k
    
    
     −
    
    
     1
    
    
     )
    
    
     ]
    
   
   
    n=[(l-1)/(k-1)]
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal">n</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">[(</span><span class="mord mathnormal" style="margin-right: 0.0197em;">l</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mclose">)</span><span class="mord">/</span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mclose">)]</span></span></span></span></span></span><br>  这意味着，给定一个固定的 kernel_size，完整覆盖所需的层数与输入张量的长度呈线性关系，这将导致网络变得非常深非常快，从而导致模型具有非常多的参数 需要更长的时间来训练。 此外，随着模型层数越多其梯度消失的问题也就很容易出现。<strong>在保持层数相对较小的同时增加感受区域大小的一种方法是将膨胀引入卷积网络</strong>。</p> 

 卷积层上下文中的扩展是指输入序列的元素之间的距离，这些元素用于计算输出序列的一个条目。 因此，传统的卷积层可以看作是 1-dilated 层，因为 1 个输出值的输入元素是相邻的。 下图显示了一个 2-dilated 层的示例，其中 input_length 为 4，kernel_size 为 3。

 与 1-dilated 的情况相比，该层的感受区域分布在 5 而不是 3 的长度上。更一般地，内核大小为 k 的 d-dilated 层的感受野分布在

    1
   
   
    +
   
   
    d
   
   
    ∗
   
   
    (
   
   
    k
   
   
    −
   
   
    1
   
   
    )
   
  
  
   1+d*(k-1)
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.7278em; vertical-align: -0.0833em;"></span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord mathnormal">d</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">∗</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mclose">)</span></span></span></span></span> 的长度上。 如果 d 是固定的，这仍然需要一个与输入张量长度呈线性关系的数字来实现完全的感受野覆盖。</p> 

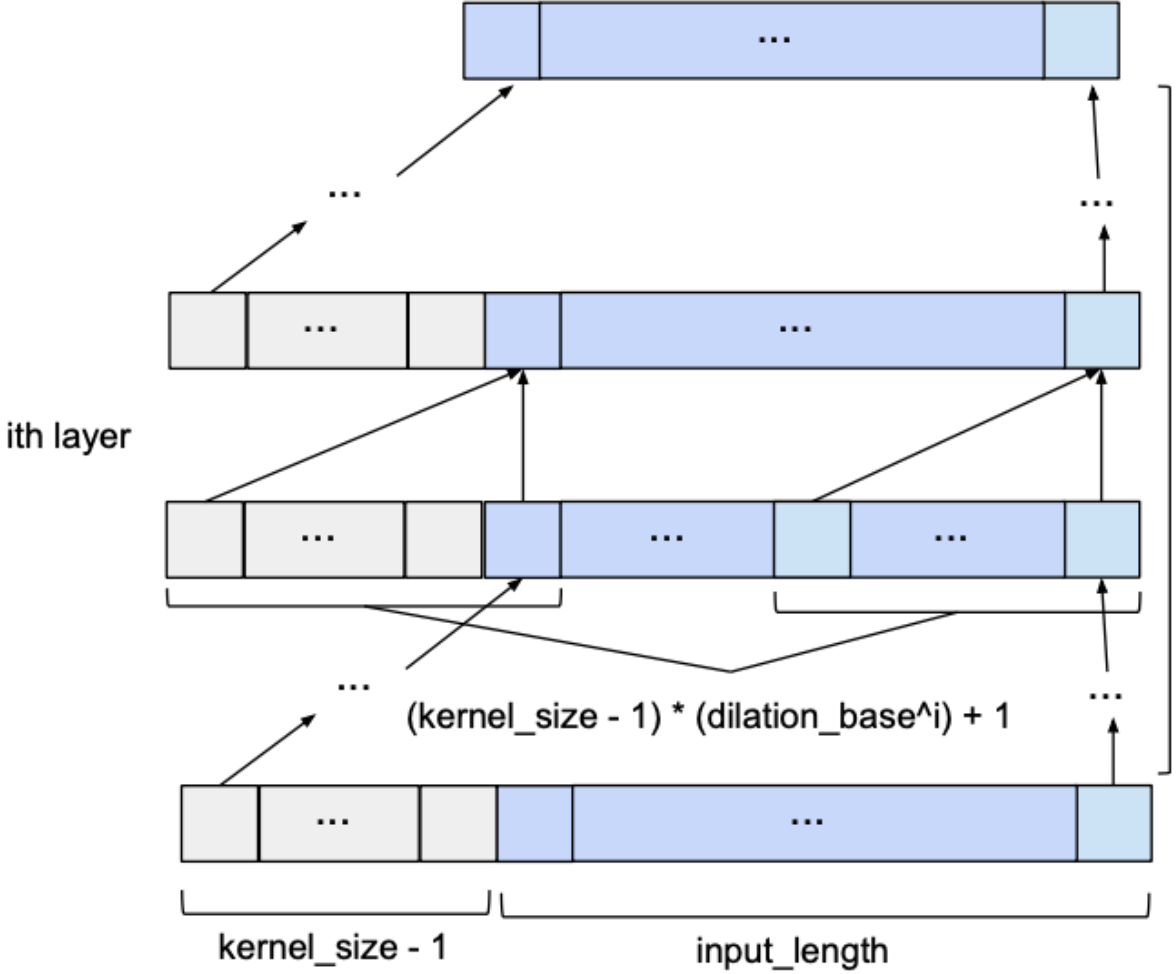
 这个问题可以通过随着我们向上移动层而以指数方式增加 d 的值来解决。 为此，我们选择一个常数 dilation_base 整数 b，它将让我们计算特定层的扩张 d 作为其下方层数 i 的函数，如

    d
   
   
    =
   
   
    
     b
    
    
     i
    
   
  
  
   d=b^i
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord mathnormal">d</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.8247em;"></span><span class="mord"><span class="mord mathnormal">b</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8247em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span></span></span></span></span></span></span></span></span>。 下图显示了一个 input_length 为 10、kernel_size 为 3 和 dilation_base 为 2 的网络，它产生了 3 个扩张卷积层以实现全覆盖。<br> <img src="https://img-blog.csdnimg.cn/img_convert/6cedc3df1ed431be6a0e7e79763352ea.png" alt=""><br>  在这里，我们只展示了输入对最后一个输出值的影响。 同样，仅显示最后一个输出值所需的零填充条目。 显然，最后一个输出值取决于整个输入覆盖范围。 实际上，给定超参数，可以使用高达 15 的 input_length，同时保持完整的感受野覆盖。 一般来说，每个额外的层都会在当前感受野宽度上增加一个 <span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    d
   
   
    ∗
   
   
    (
   
   
    k
   
   
    −
   
   
    1
   
   
    )
   
  
  
   d*(k-1)
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord mathnormal">d</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">∗</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mclose">)</span></span></span></span></span> 的值，其中 d 计算为 <span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    d
   
   
    =
   
   
    
     b
    
    
     i
    
   
  
  
   d=b^i
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord mathnormal">d</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.8247em;"></span><span class="mord"><span class="mord mathnormal">b</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8247em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span></span></span></span></span></span></span></span></span>，i 表示新层之下的层数。 因此，具有基 b 指数膨胀、内核大小 k 和层数 n 的 TCN 的感受区域 w 的宽度由下式可以计算得出：<span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     w
    
    
     =
    
    
     1
    
    
     +
    
    
     
      ∑
     
     
      
       i
      
      
       =
      
      
       0
      
     
     
      
       n
      
      
       −
      
      
       1
      
     
    
    
     (
    
    
     k
    
    
     −
    
    
     1
    
    
     )
    
    
     ⋅
    
    
     
      b
     
     
      i
     
    
    
     =
    
    
     1
    
    
     +
    
    
     (
    
    
     k
    
    
     −
    
    
     1
    
    
     )
    
    
     ⋅
    
    
     
      
       
        b
       
       
        n
       
      
      
       −
      
      
       1
      
     
     
      
       b
      
      
       −
      
      
       1
      
     
    
   
   
    w=1+\sum_{i=0}^{n-1}(k-1)\cdot b^{i}=1+(k-1)\cdot\frac{b^{n}-1}{b-1}
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal" style="margin-right: 0.0269em;">w</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.7278em; vertical-align: -0.0833em;"></span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 3.0788em; vertical-align: -1.2777em;"></span><span class="mop op-limits"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.8011em;"><span class="" style="top: -1.8723em; margin-left: 0em;"><span class="pstrut" style="height: 3.05em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">i</span><span class="mrel mtight">=</span><span class="mord mtight">0</span></span></span></span><span class="" style="top: -3.05em;"><span class="pstrut" style="height: 3.05em;"></span><span class=""><span class="mop op-symbol large-op">∑</span></span></span><span class="" style="top: -4.3em; margin-left: 0em;"><span class="pstrut" style="height: 3.05em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">n</span><span class="mbin mtight">−</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 1.2777em;"><span class=""></span></span></span></span></span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 0.8747em;"></span><span class="mord"><span class="mord mathnormal">b</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8747em;"><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">i</span></span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.7278em; vertical-align: -0.0833em;"></span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 2.1408em; vertical-align: -0.7693em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.3714em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord mathnormal">b</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mord">1</span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord"><span class="mord mathnormal">b</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.6644em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">n</span></span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mord">1</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.7693em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span></span></span>  然而，根据 b 和 k 的值，这个感受野可能有“洞”。 考虑以下具有 3 的 dilation_base 和 2 的内核大小的网络：<br> <img src="https://img-blog.csdnimg.cn/img_convert/1035783d58bb72be92b07b1b32d63bbd.png" alt=""><br>  感受区域域覆盖的范围确实大于输入大小(即15)。然而，大脑的接受野上有洞;也就是说，在输入序列中有输出值不依赖的条目(如上红色部分所示)。<strong>要解决‘漏洞’这个问题，我们需要将内核大小增加到3，或者将膨胀基数减少到2</strong>。一般来说，对于一个没有孔的接受区域，核的大小k必须至少与膨胀底b一样大。</p> 

 考虑到这些观察结果，可以计算出我们的网络需要多少层才能覆盖完整的历史记录。假设核大小为k，膨胀基数为b，其中k≥b，输入长度为l，对于全历史覆盖必须满足以下不等式:

     1
    
    
     +
    
    
     (
    
    
     k
    
    
     −
    
    
     1
    
    
     )
    
    
     ⋅
    
    
     
      
       
        b
       
       
        n
       
      
      
       −
      
      
       1
      
     
     
      
       b
      
      
       −
      
      
       1
      
     
    
    
     ⩾
    
    
     l
    
   
   
    1+(k-1)\cdot\frac{b^{n}-1}{b-1}\geqslant l
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.7278em; vertical-align: -0.0833em;"></span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 2.1408em; vertical-align: -0.7693em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.3714em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord mathnormal">b</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mord">1</span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord"><span class="mord mathnormal">b</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.6644em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">n</span></span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mord">1</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.7693em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel amsrm">⩾</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord mathnormal" style="margin-right: 0.0197em;">l</span></span></span></span></span></span>  我们可以求解 n 并获得所需的最小层数为:<span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     n
    
    
     =
    
    
     
      [
     
     
      
       
        log
       
       
        ⁡
       
      
      
       b
      
     
     
      (
     
     
      
       
        (
       
       
        l
       
       
        −
       
       
        1
       
       
        )
       
       
        ⋅
       
       
        (
       
       
        b
       
       
        −
       
       
        1
       
       
        )
       
      
      
       
        (
       
       
        k
       
       
        −
       
       
        1
       
       
        )
       
      
     
     
      +
     
     
      1
     
     
      )
     
     
      ]
     
    
   
   
    n=\left [ \log_{b}(\frac{(l-1)\cdot (b-1)}{(k-1)}+1) \right ]
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal">n</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 2.4em; vertical-align: -0.95em;"></span><span class="minner"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size3">[</span></span><span class="mop"><span class="mop">lo<span style="margin-right: 0.0139em;">g</span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.242em;"><span class="" style="top: -2.4559em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">b</span></span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.2441em;"><span class=""></span></span></span></span></span></span><span class="mopen">(</span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.427em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mord">1</span><span class="mclose">)</span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.0197em;">l</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mord">1</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mopen">(</span><span class="mord mathnormal">b</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mord">1</span><span class="mclose">)</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.936em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mord">1</span><span class="mclose">)</span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size3">]</span></span></span></span></span></span></span></span>  我们可以看到，层数现在在输入长度上是对数的，而不是线性的。 这是一个显着的改进，可以在不牺牲感受野覆盖范围的情况下实现。</p> 

 现在唯一需要指定的是每层所需的零填充条目的数量。 给定一个扩张基数 b、一个内核大小 k 和当前层以下的 i 层数，则当前层所需的零填充条目数 p 计算如下：

     p
    
    
     =
    
    
     
      b
     
     
      i
     
    
    
     ⋅
    
    
     (
    
    
     k
    
    
     −
    
    
     1
    
    
     )
    
   
   
    p=b^i\cdot(k-1)
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.625em; vertical-align: -0.1944em;"></span><span class="mord mathnormal">p</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.8747em;"></span><span class="mord"><span class="mord mathnormal">b</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8747em;"><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mclose">)</span></span></span></span></span></span></p> 

基础TCN模型

 给定 input_length、kernel_size、dilation_base 和完整历史覆盖所需的最小层数，基本的 TCN 网络看起来像这样：

预测（Forecasting）

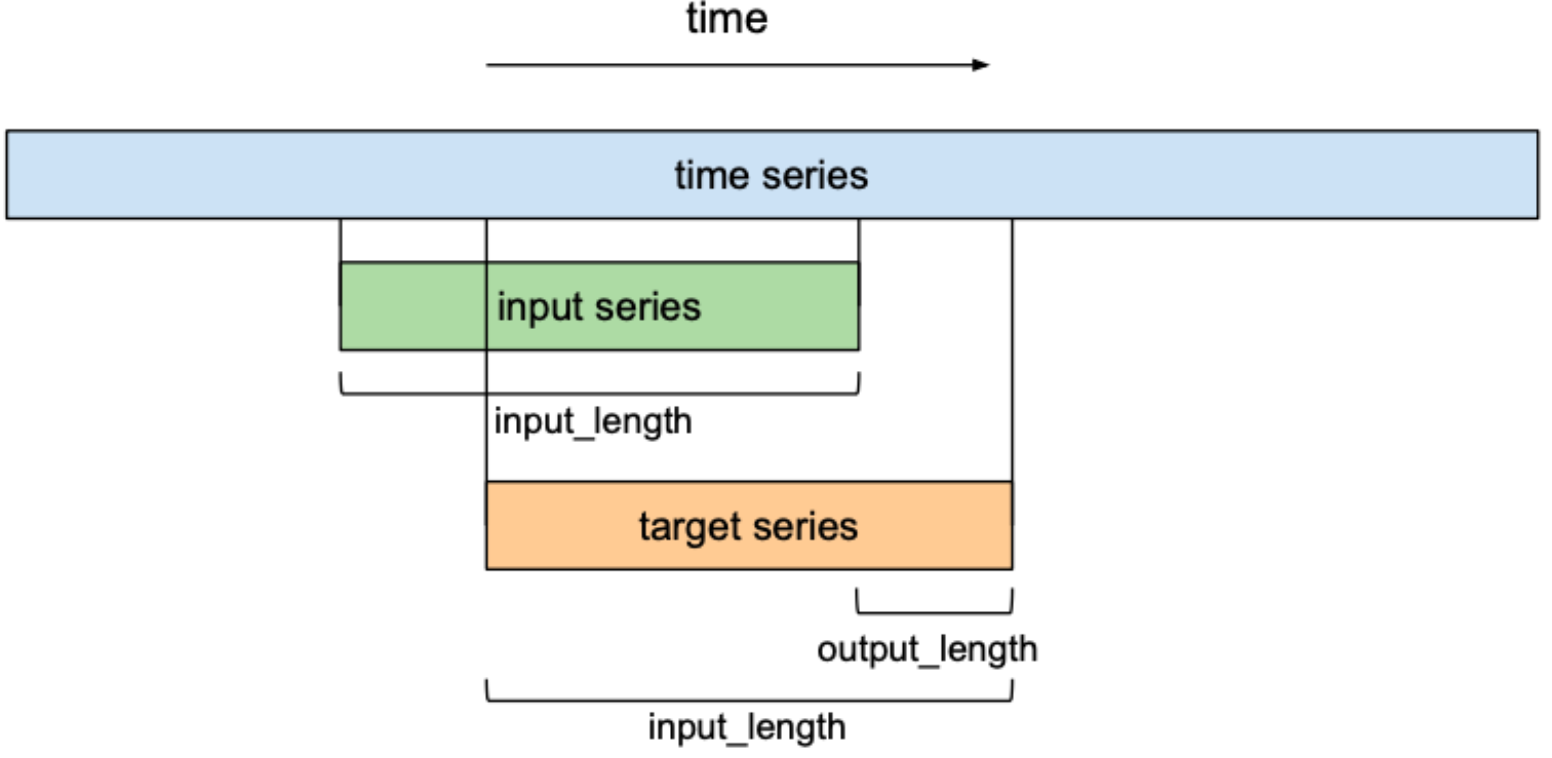
 到目前为止，我们只讨论了“输入序列”和“输出序列”，而没有讨论它们之间的关系。在上下文预测中，我们希望预测未来时间序列的下一个条目。为了训练我们的 TCN 网络进行预测，训练集将由(输入序列，目标序列)–给定时间序列的大小相等的子序列对组成。目标序列将是相对于其各自的输入序列向前移动output_length步幅的序列。这意味着长度为input_length的目标序列包含其各自输入序列的最后一个(input_length - output_length)元素作为第一个元素，而位于输入序列最后一个条目之后的output_length元素作为最后一个元素。在上下文预测中，这意味着用这种模型可以预测的最大预测范围等于output_length。使用滑动窗口方法，可以从一个时间序列中创建许多重叠的输入和目标序列对。

TCN模型升级

 S. Bai提出对基本 TCN 架构进行一些添加（即残差连接、正则化和激活函数）以提高其性能。以下对时间卷积网络的描述基于以下论文：https://arxiv.org/pdf/1803.01271.pdf

残差块

 之前介绍的基本TCN模型所做的最大修改是将模型的基本构建块从简单的一维因果卷积层更改为由具有相同扩张因子和残差连接的2层残差块。

 让我们考虑一个来自基本模型的膨胀因子 d 为 2 和内核大小 k 为 3 的层，看看它如何转化为改进模型的残差块。首先如下图：

然后变成下图：

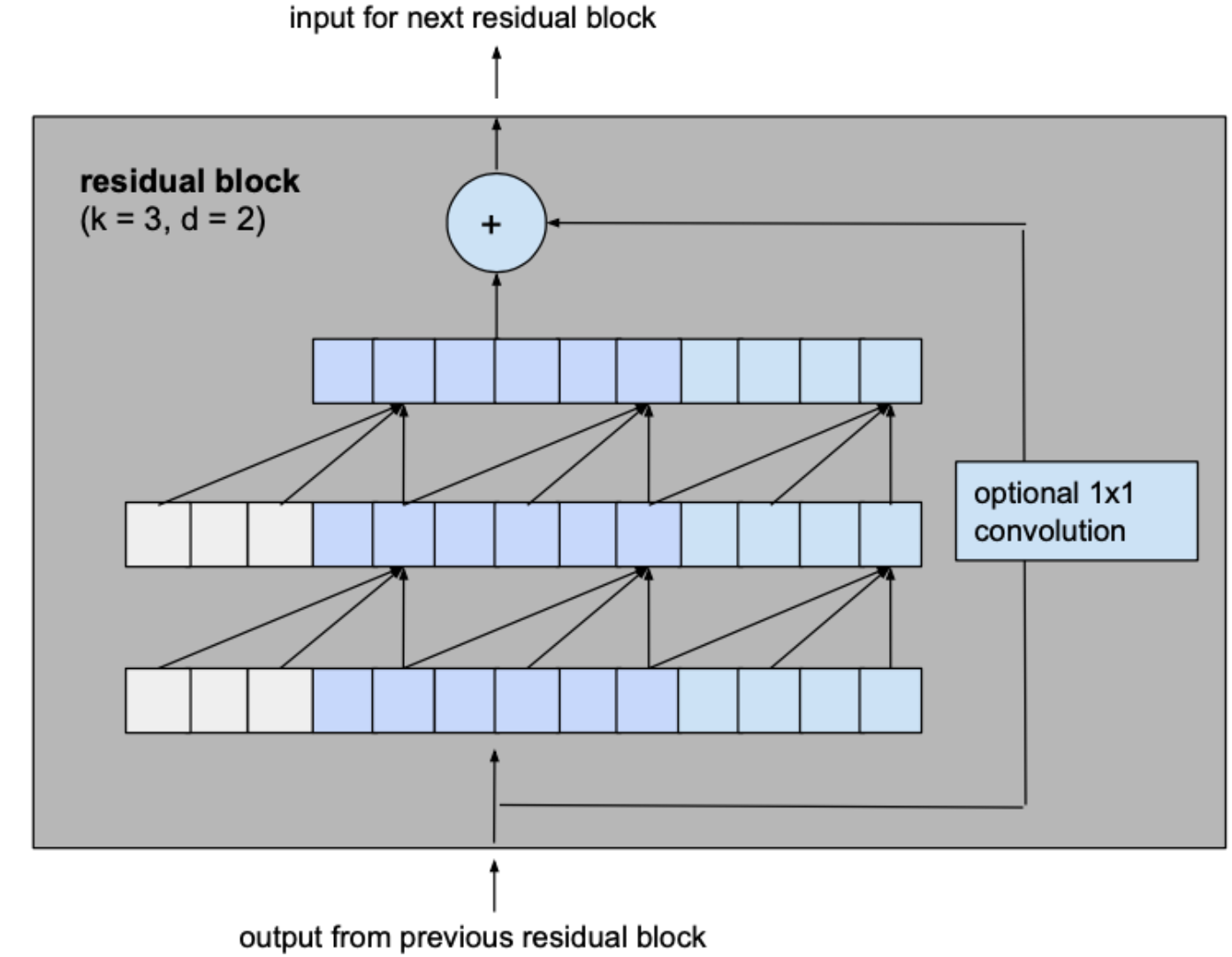
 两个卷积层的输出将被添加到残差块的输入中，以产生下一个块的输入。对于网络的所有内部块，即除了第一个和最后一个之外的所有块，输入和输出通道宽度相同，即 num_filters。由于第一个残差块的第一个卷积层和最后一个残差块的第二个卷积层可能具有不同的输入和输出通道宽度，因此可能需要调整残差张量的宽度，这是使用 1×1 卷积完成的.

 此更改会影响完全覆盖所需的最小层数的计算。现在我们必须考虑需要多少残差块才能实现完整的感受野覆盖。向 TCN 添加残差块会比添加基本因果层增加两倍的感受野宽度，因为它包括 2 个这样的层。因此，具有扩张基 b 的 TCN 的感受区域 r 的总大小、k ≥ b 的内核大小 k 和残差块的数量 n 可以计算为：

     r
    
    
     =
    
    
     1
    
    
     +
    
    
     
      ∑
     
     
      
       i
      
      
       =
      
      
       1
      
     
     
      
       n
      
      
       −
      
      
       1
      
     
    
    
     2
    
    
     ⋅
    
    
     (
    
    
     k
    
    
     −
    
    
     1
    
    
     )
    
    
     ⋅
    
    
     
      b
     
     
      i
     
    
    
     =
    
    
     1
    
    
     +
    
    
     2
    
    
     ⋅
    
    
     (
    
    
     k
    
    
     −
    
    
     1
    
    
     )
    
    
     ⋅
    
    
     
      
       
        b
       
       
        n
       
      
      
       −
      
      
       1
      
     
     
      
       b
      
      
       −
      
      
       1
      
     
    
   
   
    r=1+\sum_{i=1}^{n-1}2\cdot(k-1)\cdot b^{i}=1+2\cdot(k-1)\cdot\frac{b^{n}-1}{b-1}
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal" style="margin-right: 0.0278em;">r</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.7278em; vertical-align: -0.0833em;"></span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 3.0788em; vertical-align: -1.2777em;"></span><span class="mop op-limits"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.8011em;"><span class="" style="top: -1.8723em; margin-left: 0em;"><span class="pstrut" style="height: 3.05em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">i</span><span class="mrel mtight">=</span><span class="mord mtight">1</span></span></span></span><span class="" style="top: -3.05em;"><span class="pstrut" style="height: 3.05em;"></span><span class=""><span class="mop op-symbol large-op">∑</span></span></span><span class="" style="top: -4.3em; margin-left: 0em;"><span class="pstrut" style="height: 3.05em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">n</span><span class="mbin mtight">−</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 1.2777em;"><span class=""></span></span></span></span></span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mord">2</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 0.8747em;"></span><span class="mord"><span class="mord mathnormal">b</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8747em;"><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">i</span></span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.7278em; vertical-align: -0.0833em;"></span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 0.6444em;"></span><span class="mord">2</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 2.1408em; vertical-align: -0.7693em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.3714em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord mathnormal">b</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mord">1</span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord"><span class="mord mathnormal">b</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.6644em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">n</span></span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mord">1</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.7693em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span></span></span>这导致input_length的完整历史覆盖的最小残差块数n为：<span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     n
    
    
     =
    
    
     
      [
     
     
      
       
        log
       
       
        ⁡
       
      
      
       b
      
     
     
      (
     
     
      
       
        (
       
       
        l
       
       
        −
       
       
        1
       
       
        )
       
       
        ⋅
       
       
        (
       
       
        b
       
       
        −
       
       
        1
       
       
        )
       
      
      
       
        (
       
       
        k
       
       
        −
       
       
        1
       
       
        )
       
       
        ⋅
       
       
        2
       
      
     
     
      +
     
     
      1
     
     
      )
     
     
      ]
     
    
   
   
    n=\left [ \log_{b}(\frac{(l-1)\cdot (b-1)}{(k-1)\cdot2}+1) \right ]
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal">n</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 2.4em; vertical-align: -0.95em;"></span><span class="minner"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size3">[</span></span><span class="mop"><span class="mop">lo<span style="margin-right: 0.0139em;">g</span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.242em;"><span class="" style="top: -2.4559em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">b</span></span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.2441em;"><span class=""></span></span></span></span></span></span><span class="mopen">(</span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.427em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mord">1</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mord">2</span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.0197em;">l</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mord">1</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mopen">(</span><span class="mord mathnormal">b</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mord">1</span><span class="mclose">)</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.936em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mord">1</span><span class="mclose">)</span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size3">]</span></span></span></span></span></span></span></span></p> 

激活、归一、正则化

 为了使 TCN 不仅仅是一个过于复杂的线性回归模型，需要在卷积层之上添加激活函数以引入非线性。 ReLU 激活被添加到两个卷积层之后的残差块中。
 为了对隐藏层的输入进行归一化（这可以抵消梯度爆炸等问题），将权重归一化应用于每个卷积层。
 为了防止过拟合，在每个残差块的每个卷积层之后通过dropout引入正则化。 下图显示了最终的残差块。

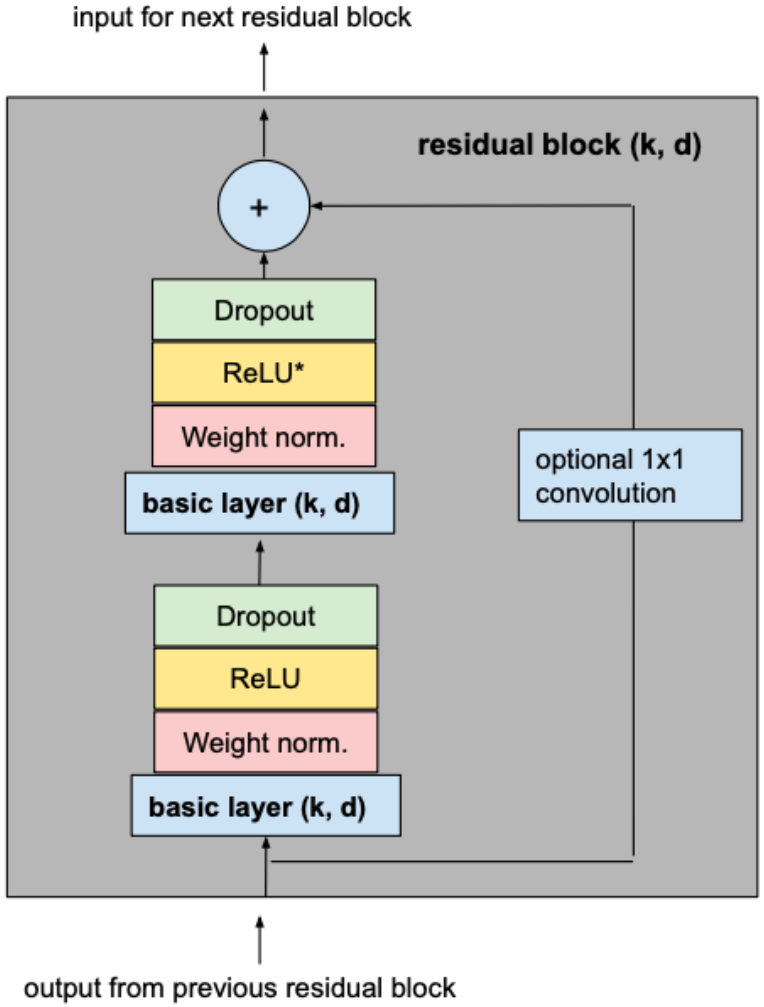
 上图中第二个 ReLU 单元中的星号表示它存在于除最后一层之外的每一层，因为我们希望最终输出也能够采用负值（这与论文中概述的架构不同）。

最终模型

 下图显示了我们最终的 TCN 模型，其中 l 等于 input_length，k 等于 kernel_size，b 等于 dilation_base，k ≥ b 并且具有完整历史覆盖 n 的最小残差块数，其中n可以根据上面参数计算出来。

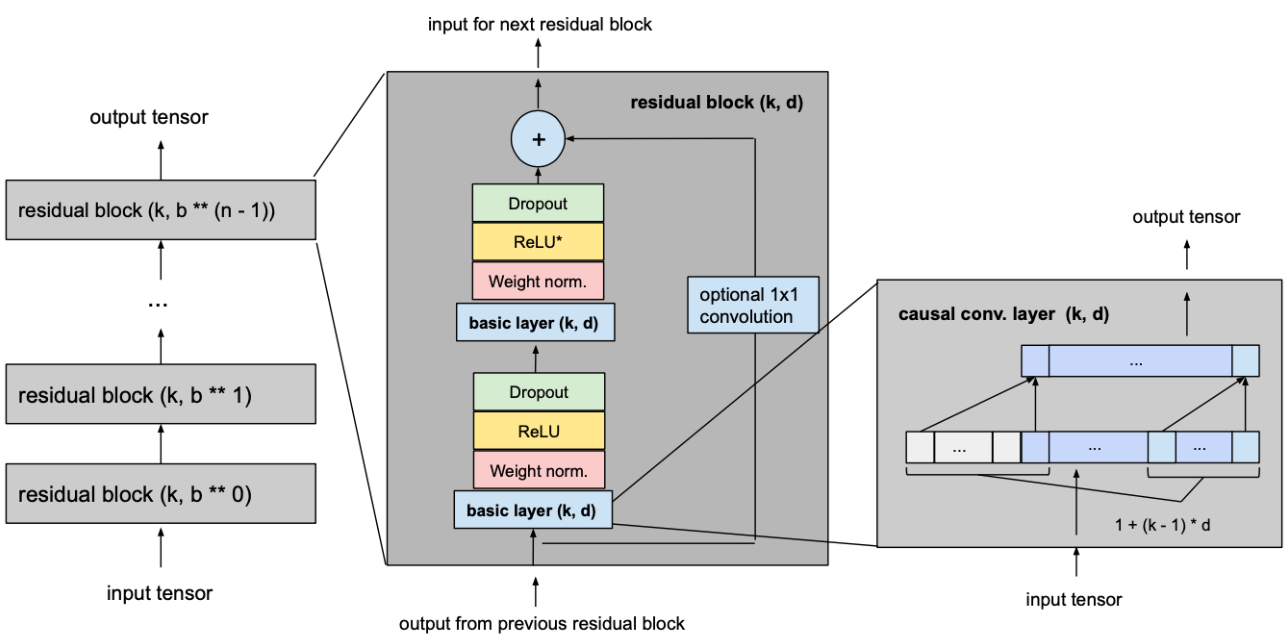
推荐阅读

[1]一文看懂线性回归【比较详细】(内含源码)
[2]一文看懂逻辑回归【比较详细】(含源码)
[3]一文了解EMNLP国际顶会 && 历年EMNLP论文下载 && 含EMNLP2022
[4]【历年NeurIPS论文下载】一文带你看懂NeurIPS国际顶会（内含NeurIPS2022）

文章知识点与官方知识档案匹配，可进一步学习相关知识

Python入门技能树人工智能深度学习 235665 人正在系统学习中