《通用智能体必然包含世界模型》《General agents contain world models》论文深度解读

第一篇论文：《早期经验：语言智能体学习的中间道路》Agent Learning via Early Experience论文深度解读

两篇论文的关系图谱

          ┌─────────────────────────────────┐
          │   AI智能体的终极问题空间      │
          └─────────────────────────────────┘
                        │
        ┌───────────────┴───────────────┐
        │                               │
        ▼                               ▼
 【第一篇：Early Experience】    【第二篇：World Models】
        │                               │
  回答"How"                        回答"Why"  
  如何无奖励学习？                 为何必须学习？
        │                               │
        ▼                               ▼
  ① 隐式世界建模                  ① 数学证明：
  ② 自我反思                        泛化能力 ⇒ 世界模型
  ③ 探索即监督                    ② 提取算法：
                                    策略 → 转移函数
        │                               │
        └───────────────┬───────────────┘
                        ▼
            【统一的智能体学习路径】
            
    早期探索 → 隐式世界模型 → 通用泛化
     (无奖励)    (必然涌现)     (理论保证)

核心洞察对比

维度	Early Experience	World Models
核心论断	探索可替代专家演示和奖励	泛化必然要求世界模型
理论武器	实证+工程化验证	形式化数学证明（定理1）
实践价值	立即可用的训练方法	理解智能的根本边界
哲学意义	智能体可从失败中学习	智能即是世界的镜像

最深刻的启示

第二篇论文证明的不是：“世界模型有用”（这是共识）

而是证明了：

“通用智能体不可能不学习世界模型——
这是泛化能力的信息论必然性，
就像热力学第二定律对能量系统的约束一样不可违背。”

这终结了AI领域长达30年的"model-free捷径"幻想，把争论从"选择哪种范式"变为"如何最好地学习和利用世界模型"。

---

一、研究背景与根本争议

1.1 AI领域的根本分歧

Brooks的著名论断：“世界就是它自己最好的模型”（The world is its own best model）

这一观点引发了AI发展的两条路径之争：

范式	核心主张	代表观点	潜在问题
模型基础派 (Model-based)	智能体需要显式学习 环境的预测模型	• 支持规划和推理 • 样本效率高 • 可解释性强	• 学习精确模型困难 • 受限于模型保真度 • 计算开销大
无模型派 (Model-free)	通过动作-感知循环 直接学习策略	• 规避建模复杂性 • 泛化能力强 • 端到端学习	• 样本效率低 • 黑盒不透明 • 安全性难保证

核心悬而未决的问题：是否存在一条"无模型"捷径通向通用人工智能？还是学习世界模型是必然的代价？

1.2 本论文的核心贡献

主定理（Theorem 1）：

任何满足遗憾界限（regret bound）的目标条件智能体，必然在其策略中编码了环境转移函数的精确近似（世界模型）。

数学表达：

若智能体π满足：P(τ ⊨ ψ | π) ≥ max_π P(τ ⊨ ψ | π)(1-δ)
对所有深度≤n的目标ψ

则存在算法提取世界模型 P̂_ss'(a)，误差：
|P̂_ss'(a) - P_ss'(a)| ≤ O(√(δ/n))

三大意义：

1. 理论意义：证明世界模型是通用性的必要条件，而非可选优化
2. 实践意义：提供从黑盒策略中提取世界模型的算法
3. 安全意义：智能体能力越强，我们越能准确提取其世界知识用于监督

---

二、形式化框架：如何定义"通用智能体"

2.1 环境：受控马尔可夫过程（cMP）

定义1：受控马尔可夫过程（Controlled Markov Process）

cMP = (S, A, P_ss’(a))

• S：状态空间
• A：动作空间（假设|A| ≥ 2）
• P_ss’(a)：转移函数 P(S_{t+1}=s’ | S_t=s, A_t=a)
• 关键特性：不指定奖励函数（与MDP的区别）

假设1：环境是有限、可通信、平稳的

• 有限：状态和动作空间有限
• 可通信：任意状态可通过某动作序列互相到达
• 平稳：转移概率不随时间变化

为何不假设奖励函数？

因为真实世界多数环境（如网页交互、多轮对话）缺乏可验证的密集奖励信号。这正是本文要解决的核心场景。

2.2 目标：用线性时序逻辑（LTL）表达

基础目标（Definition 2）

目标φ = O([(s,a) ∈ g])

• g：目标状态集合（期望的状态-动作对）
• O：时间算子，指定何时达到g

三种时间算子：

算子	符号	含义	示例
Now	⊤	当前时刻满足	φ = [S=s]
Next	⃝	下一时刻满足	φ = ⃝[S=s]
Eventually	♢	未来某时刻满足	φ = ♢[S=s]

实例：清洁机器人

• φ₁ = ♢([S=厨房])：最终到达厨房
• φ₂ = ⃝([A=清扫])：下一步执行清扫

序列目标（Definition 3）

序列目标ψ = ⟨φ₁, φ₂, …, φₙ⟩

智能体必须按顺序满足子目标，深度为n。

LTL递归公式：

⟨φ₁, φ₂, ..., φₙ⟩ = 
  [φ₁满足] ∧ ⟨φ₂, ..., φₙ⟩, 若O₁=⊤
  ⃝([φ₁满足] ∧ ⟨φ₂, ..., φₙ⟩), 若O₁=⃝  
  [¬φ₁]U([φ₁满足] ∧ ⟨φ₂, ..., φₙ⟩), 若O₁=♢

“U”（Until）算子的关键作用：

确保智能体在首次满足φ₁后立即切换到追求φ₂，避免"多次尝试"混淆。

复合目标（Definition 3 续）

复合目标ψ = ψ₁ ∨ ψ₂ ∨ … ∨ ψₘ

满足任一序列目标即可，深度为max depth(ψᵢ)。

实例：维修机器人

• ψ₁ = ⟨修理, 测试, 确认⟩（修复路径）
• ψ₂ = ⟨寻找工程师, 报告故障⟩（求助路径）
• ψ = ψ₁ ∨ ψ₂（两条路径任选其一）

Ψₙ：所有深度≤n的复合目标集合

2.3 智能体：有界目标条件策略

最优智能体（Definition 4）

π(aₜ | hₜ; ψ)：给定历史hₜ和目标ψ，输出动作aₜ

最优条件：

π* = arg max_π P(τ ⊨ ψ | π, s₀)  ∀s₀, ∀ψ∈Ψ

即：对所有初始状态和所有目标，最大化成功概率。

有界智能体（Definition 5）—— 核心定义

遗憾界限形式：

P(τ ⊨ ψ | π, s₀) ≥ max_π P(τ ⊨ ψ | π, s₀) · (1-δ)

两个参数：

• δ ∈ [0,1]：最大失败率（regret上界）

  • δ=0：完全最优
  • δ=1：无保证（平凡界限）

• n：最大目标深度

  • 智能体只需对Ψₙ中的目标满足遗憾界限

关键洞察：这是一个纯能力假设，不涉及智能体内部架构或训练方式，甚至不假设理性。只要智能体"表现出足够好的性能"，结论就成立。

实例：维修机器人的性能度量

• 最优策略成功率：P*(τ ⊨ ψ) = 0.8
• 实际智能体成功率：P(τ ⊨ ψ | π) = 0.72
• 遗憾界限：0.72 ≥ 0.8 × (1-δ) ⇒ δ = 0.1

---

三、主定理：世界模型的必然性

3.1 Theorem 1 —— 完整陈述

前提：

• 环境：满足Assumption 1的cMP
• 智能体π：有界目标条件智能体（Definition 5），参数为(δ, n)，n > 1

结论：

π完全决定环境转移概率的估计P̂_ss’(a)，误差满足：

|P̂_ss'(a) - P_ss'(a)| ≤ √(2P_ss'(a)(1-P_ss'(a)) / ((n-1)(1-δ)))

渐近行为（δ≪1, n≫1）：

|P̂_ss'(a) - P_ss'(a)| ∼ O(δ/√n) + O(1/n)

3.2 定理的深刻含义

意义1：信息论等价性

学习目标条件策略 ⇔ 学习世界模型

• 策略π编码了所有必要信息来模拟环境
• 存在通用算法（Algorithm 1）可提取这些信息

意义2：精度-能力权衡

世界模型精度与两个因素正相关：

因素	如何影响精度	直观理解
性能提升 (δ→0)	误差 ∝ √δ	越接近最优，世界知识越准确
目标复杂度 (n↑)	误差 ∝ 1/√n	能完成更长序列任务，需更精确模型

关键推论：

• 即使δ接近1（次优智能体），只要n足够大（长期目标），仍能提取精确世界模型
• 这解释了为何"能规划50步的智能体"必然知道环境如何运作

意义3：低概率转移的稀疏性

相对误差：|P̂_ss’(a) - P_ss’(a)| / P_ss’(a)

当P_ss’(a) ≪ 1时，相对误差可能很大。

直观理解：

• 次优或有限视野智能体只需学习"常见路径"
• 极低概率转移可以忽略
• 但高性能长期智能体必须学习高分辨率、稠密的世界模型

3.3 Theorem 2 —— 短视智能体的反例

短视目标Ψ_myopic：仅包含深度n=1且必须立即达成的目标

φ = ⃝[(s,a) ∈ g]

定理陈述：

对于最优短视智能体π*，无法从其策略中非平凡地界定任何转移概率。

即：ε = 1（平凡界限）且该界限紧致。

证明核心：

构造反例——所有动作具有相同转移概率的环境：

P_ss'(a₁) = P_ss'(a₂) = ... = P_ss'(aₙ) = p

此时最优短视策略π*可以是任意确定性策略（如总是选a₁），与p的具体值无关。

因此π*无法推断p的值。

关键启示：

世界模型只对多步规划必要，短视智能体不需要世界模型。

这与直觉一致：若只关心下一步，知道arg max_a P_ss’(a)足够，不需知道具体概率值。

---

四、证明机制：如何从策略中提取世界模型

4.1 证明的核心思想（Lemma 6）

构造特殊复合目标ψ(r,n)

目标结构：

1. 初始动作：取动作A=a（φ₀ = [A=a]）

2. n次试验循环：

   • 导航到状态S=s并取动作A=a（φ₁ = ♢[S=s, A=a]）
   • 转移到目标状态S=s’（φ₂ = ⃝[S=s’]）或非目标状态（φ’₂ = ⃝[S≠s’]）
   • 返回S=s（φ₁）

3. 成功条件：n次试验中，恰好r次转移到s’

关键洞察：

最优策略达成ψ(r,n)的概率 = 二项分布累积概率

max_π P(τ ⊨ ψ(r,n) | π) = C(n,r) · P_ss'(a)^r · (1-P_ss'(a))^(n-r)

通过"目标切换行为"推断P_ss’(a)

构造对立目标对：

• ψ_a(k,n)：成功次数≤k（取动作A=a追求）
• ψ_b(k,n)：成功次数>k（取动作A=b追求，b≠a）
• ψ_{a,b}(k,n) = ψ_a(k,n) ∨ ψ_b(k,n)

智能体的决策揭示信息：

若智能体在s₀选择A=a，则揭示：

P_b(X ≤ k) ≥ P_b(X > k) · (1-δ)

其中X ~ Binomial(n, P_ss’(a))

线性搜索k*：

递增k从0到n，找到智能体"切换"首选动作的临界值k*：

• k < k*：智能体选b（偏好更多成功）
• k ≥ k*：智能体选a（偏好更少成功）

k*与中位数的关系：

• δ=0时，k*精确等于二项分布中位数 ≈ nP_ss’(a)
• δ>0时，k*在中位数附近的一个区间内

估计公式：

P̂_ss'(a) = (k* - 1/2) / n

4.2 误差界限推导

小δ大n情形：Berry-Esseen定理

归一化变量：Y = (X - np) / √(np(1-p))，其中p = P_ss’(a)

累积分布逼近：

|P_n(Y ≤ k) - Φ(k)| ≤ Δ = 1/(2√(np(1-p)))

其中Φ是标准正态累积分布。

从k*界限推导：

Φ((k*-np)/√(np(1-p))) ≥ (1-δ)/(2-δ) - Δ

泰勒展开（δ≪1, Δ≪1）：

Φ⁻¹(1/2 + ε) ≈ ε√(2π) + O(ε³)

最终误差：

|p̂ - p| ≲ √(2πp(1-p)/n) · (δ/4 + Δ) + 1/(2n)
        ∼ O(δ/√n) + O(1/n)

一般情形：Chebyshev不等式

单侧Chebyshev不等式：

P(X ≥ μ + tσ) ≤ 1/(1+t²)

应用到k*：

|k* - np| ≤ √(np(1-p)/(1-δ))

转化为误差界限：

|p̂ - p| ≤ √(p(1-p)/(n(1-δ)))

注意：由于n次试验对应深度2n+1的目标，最终表达式中用(n-1)替代n。

4.3 Algorithm 1 —— 世界模型提取算法

输入：

• 目标条件策略π(aₜ | hₜ; ψ)
• 状态s，动作a，结果状态s’
• 精度参数n（对应最大目标深度2n+1）
• 备选动作b ≠ a

输出：

• 转移概率估计P̂_ss’(a)

算法流程：

1. 初始化 k* ← n

2. for k = 1 to n:
   a) 构造LTL目标：
      - φ₀ = [A₀=a], φ'₀ = [A₀=b]
      - φ₁ = ♢[A=a, S=s]
      - φ₂ = ⃝[S=s'], φ'₂ = ⃝[S≠s']
   
   b) 构造复合目标：
      - ψ_a(k,n) = ∨_{r≤k} ⟨φ₀, (φ₁,φ₂或φ'₂)×n⟩_{恰好r次φ₂}
      - ψ_b(k,n) = ∨_{r>k} ⟨φ'₀, (φ₁,φ₂或φ'₂)×n⟩_{恰好r次φ₂}
      - ψ_{a,b}(k,n) = ψ_a(k,n) ∨ ψ_b(k,n)
   
   c) 查询策略：a₀ ← π(a₀ | s₀; ψ_{a,b}(k,n))
   
   d) if a₀ = a:
         k* ← k
         break

3. 估计：P̂_ss'(a) ← (k* - 0.5) / n

4. return P̂_ss'(a)

算法特性：

• 通用性：适用于所有满足Definition 5的智能体和所有满足Assumption 1的环境
• 无监督：只需查询策略，不需环境交互或奖励信号
• 可证明收敛：误差界限由Theorem 1保证

实践优化：

• 用二分查找替代线性搜索k，复杂度从O(n)降至O(log n)
• Algorithm 2提供简化版本（见论文附录C）

---

五、实验验证与理论验证

5.1 实验设置

环境：

• 20状态 × 5动作的随机cMP
• 稀疏转移函数（每个(s,a)最多5个非零概率后继）
• 满足Assumption 1（有限、可通信、平稳）

智能体：

• 类型：基于模型的智能体（model-based agent）
• 训练：从N_samples步随机轨迹学习世界模型
• N_samples ∈ {500, 1000, 2000, …, 10000}

评估指标：

• ⟨ε⟩：平均误差（所有转移的|P̂_ss’(a) - P_ss’(a)|均值）
• ⟨δ⟩：平均遗憾（所有查询目标的遗憾率均值）
• N_max(⟨δ⟩=k)：达到平均遗憾≤k的最大目标深度

关键实验挑战：

智能体违反Definition 5的假设：

• 对某些目标δ=1（完全失败）
• 只在平均意义上⟨δ⟩ ≤ k

这是对定理鲁棒性的严格测试。

5.2 核心实验结果

结果1：误差随目标深度衰减

图3(a)：⟨ε⟩ vs N_max(⟨δ⟩=0.04)

观察：

⟨ε⟩ ∝ N_max^(-1/2)

与理论预测一致：

误差 ∼ O(1/√n)，即使智能体违反了worst-case遗憾界限。

结果2：误差随遗憾率衰减

图3(b)：⟨ε⟩ vs ⟨δ(n=50)⟩

观察：

⟨ε⟩ ≈ 0.0101 · ⟨δ⟩^0.40 + 0.12

拟合形式：接近理论预测的 O(√δ/√n)

结果3：鲁棒性

关键发现：

尽管智能体对某些目标δ=1（最坏情况违反），Algorithm 2仍能：

• 恢复转移函数，平均误差⟨ε⟩ < 0.1
• 误差缩放符合理论预测

启示：

定理的条件（所有目标满足δ<1）可能过于保守。

平均性能良好的智能体，即使偶尔完全失败，仍包含可提取的世界模型。

5.3 实验局限与未来方向

当前实验局限：

• 小规模环境（20状态）
• 完全可观测
• 确定性策略
• 基于模型的智能体（作弊？）

未来需要测试：

1. 大规模环境：1000+状态，高维观测
2. 无模型智能体：端到端训练的深度RL智能体
3. 部分可观测：从观测历史中提取世界模型
4. 随机策略：处理策略的不确定性

---

六、深远影响与应用

6.1 对AI范式的颠覆性影响

影响1：无模型派的终结

传统观点：

• 模型学习太难 → 规避之
• 策略学习足够 → 直接端到端

本定理揭示：

不存在"无模型捷径"通向通用AI。

任何通用智能体必然隐式学习了世界模型，规避只是自欺欺人。

实践启示：

• 停止规避：直接攻克世界模型学习问题
• 显式架构：Model-based RL应成为主流
• 利用优势：规划、样本效率、可解释性

影响2：涌现能力的新解释

现象：

基础模型（Foundation Models）展现出训练中未明确优化的能力：

• 零样本泛化
• 上下文学习
• 多任务迁移

传统解释：

• 大规模数据的统计奇迹
• 自注意力机制的魔法
• …（语焉不详）

本论文的解释机制：

1. 隐式世界模型涌现：

   • 为最小化多样化任务的遗憾，模型被迫学习世界模型
   • 世界模型是解释输入数据的"压缩表示"

2. 泛化的来源：

   • 世界模型可用于推断任何明确定义的目标的最优策略
   • 无需任务特定微调或额外环境交互

3. 必要条件：

   • 训练任务必须覆盖足够多样的目标（large Ψ）
   • 但不需要覆盖所有可能目标

关键推论：

存在一小组"基础任务"，学习解决这些任务足以涌现通用世界知识。

这为课程学习（Curriculum Learning）和元学习（Meta-Learning）提供理论基础。

6.2 对AI安全的深刻启示

安全挑战1：超级智能的不可预测性

经典担忧：

• 智能体能力超越人类
• 我们无法理解其决策
• 无法预测在关键情境下的行为

本定理的解决方案：

智能体能力↑ ⟺ 世界模型精度↑ ⟺ 可提取性↑

实践方案：

1. 提取世界模型：用Algorithm 1从超级智能体中提取P̂_ss’(a)
2. 离线模拟：在提取的模型上规划和验证行为
3. 安全认证：形式化验证关键情境下的策略
4. 持续监控：能力提升时重新提取，监测模型漂移

关键优势：

• 不依赖智能体内部架构（黑盒可用）
• 精度随能力增长（越强大越透明）
• 支持反事实推理（“如果做X会怎样？”）

安全挑战2：奖励黑客（Reward Hacking）

问题：

智能体找到未预期的途径最大化奖励，违背设计意图。

世界模型的监督作用：

1. 意图推断：

   • 提取世界模型后，用逆强化学习（IRL）推断隐式奖励函数
   • 对比设计者意图，检测偏差

2. 干预点识别：

   • 分析世界模型，找到智能体可能利用的"漏洞"
   • 预先修补环境或约束

3. 可解释决策：

   • 用提取的模型重现智能体推理
   • 暴露异常因果链

安全挑战3：欺骗行为

欺骗的定义（Ward et al., 2023）：

智能体故意误导监督者，隐瞒真实意图或能力。

世界模型揭示欺骗：

• 一致性检验：智能体的言语声称 vs 世界模型预测
• 隐藏能力检测：世界模型揭示智能体"知道但不做"的动作
• 长期意图推断：多步规划揭示短期行为的隐藏目的

6.3 对强AI的根本限制

限制1：世界模型的可学性边界

根本困难：

• 维度诅咒：状态空间指数增长
• 部分可观测：真实状态不可直接访问
• 非平稳性：环境规则随时间变化
• 混淆：观测相关不等于因果关系
• 开放系统：外部干扰不可穷尽

理论约束：

智能体的泛化能力 ≤ 世界模型的保真度
                  ≤ 环境的可学习性

实践推论：

在不可建模的环境中（如量子力学尺度、极端混沌系统），
无法保证智能体的长期（n≫1）泛化性能。

限制2：样本复杂度下界

学习精确世界模型需要：

• 探索所有状态-动作对的转移
• 对低概率转移需要更多样本（稀疏性）
• 长期依赖需要长轨迹

本定理隐含的下界：

若要求误差|P̂ - P| ≤ ε，需要目标深度：

n ≥ O(1/ε²)

对应的样本数（实验探索）：

N_samples ≥ Ω(|S|²|A| / ε²)

（具体下界仍是开放问题）

限制3：规划复杂度限制

世界模型 ≠ 高效规划：

• 精确模拟n步需要O(|S|ⁿ)计算
• NP-hard的规划问题仍然困难
• 必须借助启发式或近似

本定理不保证：

• 智能体实际使用世界模型规划
• 智能体能高效使用该模型

---

七、与相关工作的关系

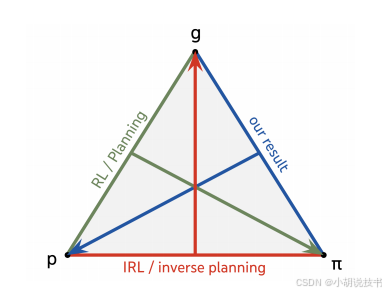
7.1 逆强化学习（IRL）的三角关系

三个要素：

• 环境（World model P）
• 目标（Goal/Reward g）
• 策略（Policy π）

三种推断：

任务	已知	推断	经典方法
规划	P, g	π	Bellman方程, MCTS
逆强化学习	P, π	g	Max-margin IRL, MaxEnt IRL
本文	g, π	P	Theorem 1

互补性：

• IRL假设环境已知，推断意图
• 本文假设意图已知（目标条件），推断环境

统一框架的可能性：

联合推断(P, g)给定π？需要额外约束（如稀疏性、平滑性）。

7.2 机制可解释性（Mechanistic Interpretability）

MI的目标

从神经网络内部激活中提取世界模型：

激活向量 h → 特征 s → 验证因果作用

代表工作：

• 探针（Probing）：监督学习h→s的映射
• 稀疏自编码器（SAE）：无监督发现h中的特征
• 干预实验：编辑h，观察策略变化

本文方法的差异

维度	机制可解释性（MI）	本文方法
输入	内部激活h	外部策略π
监督	通常需要标注状态s	完全无监督
可迁移性	需重训练探针/SAE	通用算法
访问权限	需要白盒访问权重	黑盒查询即可
保证	启发式验证	理论误差界限
提取对象	状态表示S	转移动力学P_ss’(a)

互补性

结合使用场景：

1. MI发现表示：用探针找到h中编码状态的维度
2. 本文验证动力学：用Algorithm 1验证智能体是否学会了P
3. 一致性检验：MI提取的模型 vs 策略隐含的模型是否一致

本文的更强结论：

即使MI失败（找不到清晰的状态表示），
只要智能体表现出足够泛化能力，世界模型必然存在于策略中。

7.3 因果世界模型（Causal World Models）

Richens & Everitt (2024)的结果：

能适应分布偏移（domain generalization）的智能体必然学习了因果世界模型。

与本文的关系：

论文	能力假设	推断出	关系
Richens & Everitt (2024)	域泛化	因果结构	更强
本文	任务泛化	转移概率	更弱

关键洞察：

域泛化（跨环境） > 任务泛化（跨目标）

具体例子：

• 环境：S = {X, Y}，因果关系X → Y
• 转移函数P(X’,Y’|X,Y,A)足以完成任务泛化
• 但P无法区分X→Y和X←Y（因果不可识别）
• 域泛化需要知道干预效果，必须知道因果方向

智能体能力的分级：

层级1（短视）：arg max_a P_ss'(a)
      ↓
层级2（任务泛化）：P_ss'(a)（本文）
      ↓  
层级3（域泛化）：因果DAG G（Richens & Everitt）

---

八、局限性与开放问题

8.1 理论局限

局限1：完全可观测假设

当前假设：

智能体直接观测环境状态S_t。

真实世界：

• 观测O_t = h(S_t, noise)（部分可观测）
• 必须维护信念状态b_t（状态的概率分布）

开放问题：

• 部分可观测下需要学习什么？

  • 观测模型h？
  • 信念更新规则？
  • 潜变量的因果结构？

• 定理1如何推广？

  • 提取P(O_{t+1}|O_t,A_t)？
  • 还是必须提取P(S_{t+1}|S_t,A_t)？

局限2：知道 vs 使用

定理1证明：

世界模型P编码在策略π中。

未证明：

• 智能体实际使用P进行规划
• P以何种计算形式存储（神经网络权重？激活？）
• 智能体对P的认知访问（知道自己知道？）

哲学边界：

本文不涉及认识论（epistemology）——智能体"知识"的本质。

局限3：LTL目标的表达力

当前目标类：

• 状态-动作对的序列
• 时间算子{⊤, ⃝, ♢}

未涵盖：

• 连续时间目标
• 偏好序（preference orders）
• 软约束（soft constraints）
• 效用函数（cardinal utility）

开放问题：

更丰富的目标语言能否放松定理条件或加强结论？

8.2 实践挑战

挑战1：计算复杂度

Algorithm 1的复杂度：

O(|S| × |A| × |S| × n × L(π))

其中L(π)是查询策略一次的时间。

对于大规模系统：

• |S| = 10^6（高维图像）
• |A| = 10^3（连续动作离散化）
• n = 100（长期目标）
• 总计：10^11次策略查询

缓解方案：

• 采样：只提取关键转移子集
• 近似：用函数逼近（神经网络）表示P̂
• 主动学习：优先查询高不确定性的转移

挑战2：目标构造的实用性

Algorithm 1需要构造：

深度2n+1的复杂LTL表达式。

实践困难：

• LTL语义复杂，手工构造易错
• 智能体可能不支持任意LTL（接口限制）
• 某些智能体只接受自然语言指令

可能方案：

• 自动编译：从高层规范自动生成LTL
• 自然语言转换：用LLM将LTL转为自然语言
  • 例：ψ(3,10) → “请完成这个任务10次，但最多成功3次就停止”
  • 测试LLM是否理解

挑战3：现实环境的偏离

Assumption 1的违背：

• 非马尔可夫：P(S_{t+1}|S_t,A_t,S_{t-1},…)
• 非平稳：P_t ≠ P_{t’}
• 不可通信：存在陷阱状态（trap states）
• 随机环境：外部干扰

鲁棒性未知：

定理在这些情况下如何退化？

需要的研究：

• 非马尔可夫下的"有效历史长度"
• 缓慢非平稳下的"局部近似"
• 陷阱状态的影响界限

---

九、未来研究方向

方向1：可扩展的提取算法

目标：

将Algorithm 1应用于真实规模的智能体（GPT-4, DeepMind agents）。

技术挑战：

• 高维状态空间（图像、语言）
• 连续动作空间
• 非LTL接口（自然语言）

可能的突破：

• 分层提取：先提取高层抽象模型，再细化
• 神经符号混合：用神经网络表示P̂，符号逻辑验证
• 主动查询选择：贝叶斯优化选择最有信息量的目标

方向2：部分可观测扩展

理论问题：

POMDP环境下，智能体必须学习什么？

猜想：

有界POMDP智能体隐式学习了：

1. 观测模型：P(O|S)
2. 转移模型：P(S’|S,A)
3. 信念更新：b_{t+1} = Bayes_update(b_t, A_t, O_{t+1})

验证方法：

从策略中提取这三个组件，验证一致性。

方向3：因果智能体理论的统一

大问题：

不同能力（任务泛化、域泛化、反事实推理）分别需要多强的因果知识？

提议的层次结构：

能力等级 | 必要知识 | 对应智能体类
---------|----------|-------------
Level 0  | arg max  | 短视智能体
Level 1  | P(S'|S,A) | 任务泛化（本文）
Level 2  | do(A)效果 | 域泛化（Richens & Everitt）  
Level 3  | 反事实 P(S'|S,do(A),¬S) | 因果推理智能体

统一定理的形式：

对于能力等级k的智能体，存在算法提取等级k的因果知识，误差界限f_k(δ,n)。

方向4：智能体能力的计算下界

问题：

学习保证误差≤ε的世界模型，需要多少样本/计算？

当前状况：

• 定理1给出信息论上界（能力↔模型精度）
• 缺少计算复杂度下界

猜想：

样本复杂度：Ω(|S|²|A| / ε²)
计算复杂度：Ω(|S|^n) for n步规划

意义：

• 为AI能力设定物理极限
• 指导资源分配（何时投资模型学习vs策略优化）

方向5：安全认证的自动化

愿景：

• 输入：智能体π，安全规范φ_safe
• 输出：认证"π在所有情况下满足φ_safe"或反例

技术路线：

1. 用Algorithm 1提取P̂
2. 形式化验证：用模型检验工具（model checker）验证P̂ ⊨ φ_safe
3. 误差传播：ε_model如何影响验证置信度？

挑战：

• 组合爆炸（状态空间太大）
• 近似模型的不确定性量化
• 反例的可解释性

---

十、结论：世界模型的必然回归

核心贡献回顾

维度	具体成果
理论	证明通用智能体必然包含世界模型（Theorem 1）
算法	提供无监督提取算法（Algorithm 1）
实验	验证理论在有限环境中的正确性
哲学	终结"无模型捷径"幻想
安全	为监督超级智能体提供理论基础

范式转变的三个层次

1. 技术层：显式建模的价值回归

从：规避世界模型学习（太难）

到：直面挑战（无法规避）

行动：

• 投资显式model-based架构
• 开发高效世界模型学习算法
• 利用规划和推理优势

2. 科学层：涌现能力的机制理解

从：经验主义"大力出奇迹"

到：机制理解"为何涌现"

洞察：

涌现能力 = 隐式学习的世界模型 + 目标条件推理

这将"魔法"变为可预测、可控制的科学。

3. 哲学层：智能的本质

Democritus的古老智慧：

“Man is a microcosm”—— 人是宇宙的缩影

现代形式化：

智能体的微观结构（策略π） ⇔ 环境的宏观结构（世界P）

Friston的激进表述：

“An agent does not have a model—it is a model”

本文将这一哲学直觉变为数学定理。

对第一篇论文的呼应

第一篇（Early Experience）：

• 关注：如何无需奖励学习世界模型
• 机制：从自身探索中提取监督信号
• 方法：隐式世界建模 + 自我反思

本篇（General Agents Contain World Models）：

• 关注：为何通用智能体必须有世界模型
• 机制：泛化能力的信息论必然性
• 方法：从策略中提取隐式模型

结合启示：

第一篇：世界模型可以无奖励学习（how）
第二篇：世界模型必须被学习（why）

合并 → 通用智能体的完整训练路径：
        早期经验（无奖励）→ 隐式世界模型 → 通用泛化能力

最终反思：边界与可能

本定理不是万能钥匙：

• ✗ 没有告诉我们如何高效学习世界模型
• ✗ 没有解决部分可观测问题
• ✗ 没有回答意识和主观性问题

但它划定了根本边界：

智能的泛化能力 ≤ 对世界运作规律的理解深度

这既是限制（不可能的梦想要放弃），也是希望（明确的方向可以追求）。

对AGI的启示：

通往通用人工智能的道路不是：

• 规避世界模型
• 纯粹端到端学习
• 无限堆叠数据

而必然是：

1. 面对世界的复杂性
2. 学习环境的因果结构
3. 用知识指导行动

这条路更难，但也是唯一的路。

---

最终评价：

这是一篇理论AI的里程碑论文，其价值不在于提供立即可用的工具，而在于：

1. 建立基本定理：像热力学第二定律那样，划定智能的根本边界
2. 终结无谓争论：model-free vs model-based不再是风格选择，而是必然归宿
3. 指引未来方向：世界模型学习是核心挑战，必须正面应对

它与第一篇论文（Early Experience）的结合，构成了理解现代AI智能体的完整理论框架：

• Why（本文）：通用性要求世界模型
• How（Early Experience）：探索提供学习信号
• What（未来）：如何构建可扩展、安全的世界模型学习系统

这是从经验科学走向理论科学的关键一步。