0. 前言
奇偶校验(Parity Check)码,是一种二进制数字信息在传输或存储过程中实现错误检测的编码技术,Richard Wesley Hamming于1950年发表的论文《Error Detecting and Error Correcting Codes》中,明确提出了这一单比特检错码(Single error detecting codes),并将这种检错方法命名为:parity check。 [*笔者并不能确认奇偶校验是由R. W. Hamming发明的,写在此处,仅作为一个事实的陈述*]
本文的核心内容是向读者介绍用于单比特奇偶校验码三个概率的精确而又极为简单的计算公式:
- 无差错概率: \( P_0=(1- \epsilon)^n \);
- 差错检出概率: \( P_d=0.5-0.5(1- 2\epsilon)^n \);
- 差错漏检概率:\( P_{ud}=0.5+0.5(1- 2\epsilon)^n -(1- \epsilon)^n \)。
为获得上述三个公式,本文将包括(但不限于)以下一些基础概念,为避免不必要的阅读困扰,特先列出相关引用(正文中将不加标注地直接引用):
- 信道(Communication Channel);
- 分组码(Block Code);
- 线性分组码(Linear Block Code);
- 汉明重量(Hamming Weight);
- 汉明距离(Hamming Distance)、最小汉明距离(Minimum Hamming Distance);
- 二元对称信道(BSC,Binary Symmetric Channel);
- 二项分布(Binomial Distribution);
- 二项式定理(Binomial Theorem)、二项式公式(Binomial Formula or Binomial Identity)、二项展开式(Binomial Expansion);
- 二项式系数(Binomial Coefficient);
提示:文中公式较多,可能出现显示不完整的现象,请刷新页面重试!用手机访问试了一下,没有电脑页面的阅读效果好!
1. 单比特奇偶校验码的基本原理
单比特奇偶校验码的编码原理为:在待编码的 \( k(\geqslant 1) \) 位二进制序列中添加1个比特的冗余位,使得编码后长度为 \( n(=k+1) \) 的码字中“1”的个数为奇数(Odd)或偶数(Even)。设待编码的二进制序列为\( D[d_{k-1},...,d_{0}] \),编码完成的码字为\( C[d_{k-1},...,d_{0},p] \),有:
- 奇校验时,\( p=!(d_{k-1}\oplus...\oplus d_{0}) \),也可写为\( p=d_{k-1}\oplus ... \oplus d_{0} \oplus 1 \),或写为\( d_{k-1}\oplus ... \oplus d_{0} \oplus p=1 \);
- 偶校验时,\( p=(d_{k-1}\oplus...\oplus d_{0}) \),也可写为\( p=d_{k-1}\oplus ... \oplus d_{0} \oplus 0 \),或写为\( d_{k-1}\oplus ... \oplus d_{0} \oplus p=0 \)。
奇偶校验的编/译码过程也可用文字描述为:
- 奇校验时,含校验位在内的整个码字中“1”的个数(即码字的汉明重量)为奇数。若信息位中“1”的个数为奇数,则校验位为“0”,反之则校验位为“1”;
- 偶校验时,含校验位在内的整个码字中“1”的个数(即码字的汉明重量)为偶数。若信息位中“1”的个数为奇数,则校验位为“1”,反之则校验位为“0”。
奇偶校验码的一些性质(特征):
- 奇校验不会生成全 0 码字,\( n \) 为偶数时,奇校验不会生成全 1 码字;
- 偶校验可以生成全 0 码字,\( n \) 为奇数时,偶校验不会生成全 1 码字;
- 奇校验许用码字的汉明重量为奇数,偶校验许用码字的汉明重量为偶数;
- 奇偶校验码在定义上属于分组码(Block Code),可记为\( C(n,k) \);
- 偶校验码在定义上属于线性分组码(Linear Block Code);
- 奇校验码在定义上不属于线性分组码。例如\( (0001)_{2} \)、\( (0010)_{2} \)是奇校验码\( C(4,3) \)的两个许用码字,但\( (0001)_{2} \oplus (0010)_{2} = (0011)_{2} \),两个许用码字的线性组合生成的新码字\( (0011)_{2} \)不属于许用码字,这违背了线性分组码的定义。一般地,奇校验码字集合中,奇数个许用码字的线性组合(\( \oplus \))仍是许用码字;偶数个许用码字的线性组合(\( \oplus \))不是许用码字;
- 奇偶校验码的最小汉明距离\( d_{min}=2 \)。
2. 一些不是问题的问题
2.1 为什么说单比特奇偶校验码的最小汉明距离等于2?
令\( x \)为奇偶校验码某(任意一个)许用码字\( C_{x} \)中“1”的个数,若只改变该码字的一位,则新码字\( C_{y} \)中“1”的个数(不妨设为\( y \))为\( y=x\pm 1 \),\( x、y \)的奇偶性相异,可知新码字\( C_{y} \)不是该奇偶校验码的许用码字,即奇偶校验的码字集合中任意两个码字的汉明距离不等于1。若改变该码字中的任意两位(设为\( a、b \)),则新码字\( C_{y} \)中“1”的个数为:
- 当\( a、b \)均由\( 0\rightarrow 1 \)时,\( y=x+2 \);
- 当\( a、b \)均由\( 1\rightarrow 0 \)时,\( y=x-2 \);
- 当\(a\)由\( 0\rightarrow 1 \)、\(b\)由\( 1\rightarrow 0 \)时,\( y=x \);
- 当\(a\)由\( 1\rightarrow 0 \)、\(b\)由\( 0\rightarrow 1 \)时,\( y=x \)
\( x、y \)的奇偶性相同,可知新码字\( C_{y} \)是该奇偶校验码的许用码字,即奇偶校验的码字集合中存在两个码字的汉明距离等于2。
综合起来就是:长度为\(n\)比特的奇偶校验码\( C(n,n-1) \),可以证明其许用码字集合中存在汉明距离等于2的码字,不存在汉明距离等于1的码字,故该码字集合的最小汉明距离为2。没有为什么了,这是定义。
2.2 单比特奇偶校验只能检测“奇数个错误比特的错误”,就没有例外?
上述推导单比特奇偶校验码最小汉明距离的过程可进一步地一般化,若改变奇偶校验码某(任意一个)许用码字\( C_{x} \)中任意的\( (g+h) \)个比特,则新码字\( C_{y} \)中“1”的个数为:
- 当\( (g+h) \)个比特均由\( 0\rightarrow 1 \)时,\( y=x+(g+h) \);
- 当\( (g+h) \)个比特均由\( 1\rightarrow 0 \)时,\( y=x-(g+h) \);
- 当其中\(g\)个比特由\( 0\rightarrow 1 \)、而\(h\)个比特由\( 1\rightarrow 0 \)时,\( y=x+g-h=x-2h+(g+h) \);
- 当其中\(g\)个比特由\( 1\rightarrow 0 \)、而\(h\)个比特由\( 0\rightarrow 1 \)时,\( y=x-g+h=x-2g+(g+h) \)
可以知道,\( x、y \)奇偶性之间的(异/同)关系由\( (g+h) \)的奇偶性决定,即由我们改变的总比特数决定:
- 当\( (g+h) \)为奇数,即奇偶校验码的码字中出现“奇数个错误比特”时,新码字汉明重量的奇偶性与原码字相异,即新码字不符合对应的奇(或偶)校验规则,奇偶校验可检测出码字中“奇数个错误比特”的错误;
- 当\( (g+h) \)为偶数,即奇偶校验码的码字中出现“偶数个错误比特”时,新码字汉明重量的奇偶性与原码字相同,即新码字符合对应的奇(或偶)校验规则,奇偶校验不能检测出码字中“偶数个错误比特”的错误。
2.3 单比特奇偶校验码不能检测突发错误?
数字通信中的“突发错误(Burst-Error)”指的是连续传输的二进制位流中一段连续的错误,通常由通信的外部干扰导致,突发错误以首、末两个错误位界定,不关心此两位之间的比特是否错误,如下图所示:
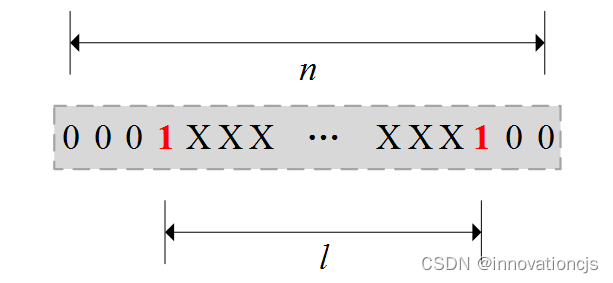
突发错误所覆盖的全部(含首、末错误位)比特数量,称为突发长度\( l \),人们分析检错编码的突发错误检测能力时,通常依据突发错误的长度,考虑这个长度下可能的\( 2^{l-2} \)个错误图样中,检错编码是否能提供相对随机错误检测额外的检测能力?从前文对“单比特奇偶校验码可检出错误图样码型和不可检出错误图样码型”的分析可知,单比特奇偶校验码针对突发错误没有提供额外的检测能力,仍然是:突发错误导致码字中出现奇数个错误比特,则能检测出该错误,反之不能检出。
2.4 奇校验还是偶校验,怎么选?
奇、偶校验在二元对称信道下的差错检测性能完全一致!二者是否属于线性分组码不影响差错检测性能。
二者能否生成“全0”、“全1”这两个特殊码字,在某些特定系统中针对开、短路的特定电路故障可能会带来些许优势。这个特性属于“就事论事”,没有一般性原则,笔者工作中并未接触到这样特定的系统,所以举不出实例。
“异步通信用偶校验,同步通信用奇校验”这个说法有正经来源吗?还真有,见ISO 1177-1985(E). Information processing — Character structure for start/stop and synchronous character oriented transmission:

规范中并未给出如此区分的原因。至于非要解释,就是“仁者见仁、智者见智”了,毕竟没有标准答案的东西,能自圆其说就好。
3. 单比特奇偶校验的检错性能
奇偶校验作为一种“二进制数字信息传输或存储”过程中的差错检测手段,对其检错性能需要进行评估。依评价的参数维度、标准、手段等通常分为两类。
3.1 差错检出比例Kd
以差错的比特数量为研究对象,区分出不同的差错类别,如:错误比特数量为奇数、错误比特数量为偶数、3个比特的随机错误、5个比特的连续错误……,通常用于检错性能的定性分析。有时也定量地描述为“某种差错类别的可检出数量”占“此种错误类别总数量”的比例,即差错检出比例\( K_{d} \)(the Fraction of Detected Error)。
信息位长度为\( k \),码字长度\( n=k+1 \)的单比特奇偶校验码,依据奇偶校验的原理,码字中(含校验位在内)的错误比特数量:
- 为奇数时,奇偶校验能发现(检出)此错误;
- 为偶数时,奇偶校验不能发现(检出)此错误。
对于经常被放在一起比较的奇偶校验、累加和校验、CRC校验,或因其不具备纠错能力、或纠错能力较差、或纠错译码代价大等原因,在实际工程中基本只用于差错检测。三者在原理上都属于二进制分组码,即在\( k \)位信息码的基础上,添加\( r \)位的冗余(监督)码,编码成\( n=k+r \)位的消息码,记为\( (n,k) \),从而将原\( 2^k \)个码字的信息码空间,扩张为\( 2^n \)个码字的消息码空间(其中\( 2^k \)个许用码字,\( 2^n-2^k \)个禁用码字)。信息发送端按规定的编码规则将发送的信息码映射(并限制)于许用码字空间,接收端将按相同的规则识别收到的消息码位于整个码空间的哪个区域,进而判定收到的消息是否正确:
- 若位于\( 2^k \)个码字的许用空间内,判定消息正确;
- 若位于\( (2^n-2^k) \)个码字的禁用空间内,判定消息错误。
\( n \)比特二进制序列构成\( 2^n \)个码字的消息码空间,是一个封闭的线性空间,在认为差错只引起消息中的比特状态翻转(0→1或1→0)的条件下,可能的差错总数量为\( 2^n-1 \),其中:
- \( (2^n-2^k) \) 种错误将导致接收端收到的码字位于禁用码字空间,可正确的检出错误;
- \( (2^k-1) \)种错误将导致接收端收到的码字位于许用码字空间,不能检出错误。
综上,对于\( (n,k) \)二进制分组码,\( n、k \)相同时,包括奇偶校验码、累加和校验码、CRC校验码在内,它们的差错检出比例\( K_d \)(或漏检比例\( K_{ud} \))是相同的:
\[ \begin{aligned}
K_{ud}&=\frac{2^k-1}{2^n-1}\approx 2^{-(n-k)} \\
K_{d} &=\frac{2^n-2^k}{2^n-1}\approx 1-2^{-(n-k)}
\end{aligned} \]
3.2 差错漏检概率Pud
差错漏检概率\( P_{ud} \)(the Probability of Undetected Error, Undetected Error Probability),也称为残余差错概率\( P_{re} \)(Residual Error Probability),指“错误已经发生,但是检测手段不能发现此错误”这一事件发生的概率。
以“传输过程中是否出错?以及出错时能否检测出错误?”为研究对象,其种类是可枚举的,共计三种,分别对应三个概率:
- 无差错概率\( P_0 \),即“接收端收到的码字中每个比特都正确”的概率,此概率越大越好;
- 差错检出概率\( P_d \),即“接收端收到的码字中有错误,但该错误能被发现(检出)”的概率,此概率越小越好(这不是笔误,因为检出差错首先意味着出错了,当这个(差错检出)概率大到等于1时,意味着100%确信收到的消息都是错的,那这样的系统是好还是不好呢?);
- 差错漏检概率\( P_{ud} \),即“接收端收到的码字中有错误,且该错误不能被发现(检出)”的概率,此概率越小越好。
依上述三个概率的定义可知,三者之和恒为1(\( P_0+P_d+P_{ud}\equiv 1 \))。
事实上,对于差错检测而言,几乎不太可能做到检出所有(100%)的错误,意即检测手段给出“无错”结论时,这一结论本身很难做到100%的置信度。因此,人们评价一种检错手段的性能时,通常真正关心的是“未能检出已发生错误”的概率,显然,这个概率越小越好!
更进一步的,“无差错概率\( P_0 \)”和“差错漏检概率\( P_{ud} \)”是“可靠通信”的两个关键因素,二者既有先后之分,也有主次之分,故而人们研究“可靠通信”时总是将“无差错概率\( P_0 \)”作为主要矛盾来对待,总是致力于优先实现误比特概率最小化的通信物理层,但差错总是不可避免的(这话的潜台词是“有错,但不多”),于是人们引入差错检测手段,当发现错误时,接收方可选择丢弃错误的消息或请求发送方重发消息,这个过程中最害怕的事儿自然是:“有错,但没发现”,所以,研究奇偶校验、累加和校验、CRC校验等差错检测编码时,请别忘了给它们一个足够小的信道误比特概率。
4. 单比特奇偶校验码的概率计算
误比特率为\( \epsilon \)的二元对称信道(BSC,Binary Symmetric Channel)下,接收端收到的长度为\( n(n\geqslant 2) \)的码字中,包含\( i(0 \leqslant i \leqslant n ) \)个随机错误比特的概率是典型的二项分布(Binomial Distribution),其发生概率为\( P(i;n,\epsilon )=\binom{n}{i} \epsilon ^i(1- \epsilon )^{n-i} \),式中\( \binom{n}{i}=C_{n}^{i}=\frac{n!}{i!(n-i)!} \)为“\( n \)中取\( i \)”的组合数,称为二项式系数(Binomial Coefficient)。
4.1 依定义计算单比特奇偶校验的概率
当\( i=0 \)时,是为无差错概率:
\[ P_0=\binom{n}{0}\epsilon ^0(1-\epsilon)^{n-0}=(1-\epsilon)^{n} \]
因所有错误比特数量为奇数的错误都可以被奇偶校验发现(检出),故奇偶校验的差错检出概率\( P_d \)为二项分布中奇数项之和,如下式(其中\( \left \lceil x \right \rceil \)表示向上取整):
\[ \begin{aligned}
P_d &=\sum_{i=1}^{\left \lceil n/2 \right \rceil}\binom{n}{2i-1}\epsilon ^{2i-1}(1-\epsilon )^{n-2i+1} \\
&=(1-\epsilon )^n \sum_{i=1}^{\left \lceil n/2 \right \rceil}\binom{n}{2i-1}(\frac{\epsilon }{1-\epsilon })^{2i-1} \\
&=\binom{n}{1}\epsilon ^1(1-\epsilon )^{n-1}+\binom{n}{3}\epsilon ^3(1-\epsilon )^{n-3}+\binom{n}{5}\epsilon ^5(1-\epsilon )^{n-5}+...
\end{aligned} \]
因所有错误比特数量为偶数的错误都不能被奇偶校验发现(检出),故奇偶校验的差错漏检概率\( P_{ud} \)为二项分布中(大于0的)偶数项之和,如下式(其中\( \left \lfloor x \right \rfloor \)表示向下取整):
\[ \begin{aligned}
P_{ud} &=\sum_{i=1}^{\left \lfloor n/2 \right \rfloor}\binom{n}{2i}\epsilon ^{2i}(1-\epsilon )^{n-2i} \\
&=(1-\epsilon )^n \sum_{i=1}^{\left \lfloor n/2 \right \rfloor}\binom{n}{2i}(\frac{\epsilon }{1-\epsilon })^{2i} \\
&=\binom{n}{2}\epsilon ^2(1-\epsilon )^{n-2}+\binom{n}{4}\epsilon ^4(1-\epsilon )^{n-4}+\binom{n}{6}\epsilon ^6(1-\epsilon )^{n-6}+...
\end{aligned} \]
4.2 单比特奇偶校验概率计算的简化公式
依照单比特奇偶校验各概率的定义及二项分布的原理,直接获得的计算公式中,无差错概率\( P_0 \)的公式倒是很简单,但差错检出概率\( P_d \)和漏检概率\( P_{ud} \)的公式就不那么友好了,会编制程序还行,\( n \)较小时用EXCEL处理也能忍,实在不行就只有“工程近似”了,舍弃公式后面的“较小项”,但多小算小?1%?0.1%?0.01%?没有一个标准,完全看心情。
那有没有可能这两个概率(\( P_d \)、\( P_{ud} \))也有着和\( P_0 \)一样简单的公式呢?还真有!
依据二项式公式(Binomial Formula or Binomial Identity),其中\( a、b \)为实数,\( n \)为非负整数:
\[ (a+b)^n=\sum_{i=0}^{n}\binom{n}{i}a^{i}b^{n-i}=\sum_{i=0}^{n}\binom{n}{i}a^{n-i}b^{i} \]
可得如下\( 1^n \)和\( (1-2\epsilon)^n \)的二项展开式(Binomial Expansion):
\[ \begin{aligned}
1^n &= [(1-\epsilon ) + \epsilon ]^n \\
&= \sum_{i=0}^{n}\binom{n}{i}\epsilon ^{i}(1-\epsilon )^{n-i} \\
&=\binom{n}{0}\epsilon ^{0}(1-\epsilon )^{n-0} +
\binom{n}{1}\epsilon ^{1}(1-\epsilon )^{n-1} + ... +
\binom{n}{n}\epsilon ^{n}(1-\epsilon )^{0} \\
(1-2\epsilon )^n &= [(1-\epsilon ) - \epsilon ]^n \\
&= \sum_{i=0}^{n}\binom{n}{i}(-\epsilon) ^{i}(1-\epsilon )^{n-i} \\
&=\binom{n}{0}(-\epsilon) ^{0}(1-\epsilon )^{n-0} +
\binom{n}{1}(-\epsilon) ^{1}(1-\epsilon )^{n-1} + ... +
\binom{n}{n}(-\epsilon) ^{n}(1-\epsilon )^{0}
\end{aligned} \]
将\( 1^n \)和\( (1-2\epsilon)^n \)的二项展开式相加,再除以2,可求得二项分布的偶数项之和(等于单比特奇偶校验码的无差错概率\( P_0 \)与差错漏检概率\( P_{ud} \)之和):
\[ \begin{aligned}
1+(1-2\epsilon )^{n} &= 2\binom{n}{0}\epsilon ^{0}(1-\epsilon )^{n} +
2\binom{n}{2}\epsilon ^{2}(1-\epsilon )^{n-2} +
2\binom{n}{4}\epsilon ^{4}(1-\epsilon )^{n-4} +... \\
\frac{1+(1-2\epsilon )^{n}}{2} &=\sum_{i=0}^{\left \lfloor n/2 \right \rfloor}\binom{n}{2i} \epsilon ^{2i} (1- \epsilon)^{n-2i} \\
&=P_0+P_{ud}
\end{aligned} \]
将\( 1^n \)和\( (1-2\epsilon)^n \)的二项展开式相减,再除以2,可求得二项分布的奇数项之和(等于单比特奇偶校验码的差错检出概率\( P_d \)):
\[ \begin{aligned}
1-(1-2\epsilon )^{n} &= 2\binom{n}{1}\epsilon ^{1}(1-\epsilon )^{n-1} +
2\binom{n}{3}\epsilon ^{3}(1-\epsilon )^{n-3} +
2\binom{n}{5}\epsilon ^{5}(1-\epsilon )^{n-5} +... \\
\frac{1-(1-2\epsilon )^{n}}{2} &=\sum_{i=1}^{\left \lceil n/2 \right \rceil}\binom{n}{2i-1} \epsilon ^{2i-1} (1- \epsilon)^{n-2i+1} \\
&=P_d
\end{aligned} \]
综上,码字(含1位校验位)长度为\( n(\geqslant 2) \)的单比特奇偶校验码,其无差错概率\( P_0 \)、差错检出概率\( P_d \)、差错漏检概率\( P_{ud} \)的计算公式分别为(其中\( \left \lceil x \right \rceil \)表示向上取整,\( \left \lfloor x \right \rfloor \)表示向下取整):
\[ \begin{aligned}
P_0 &=\sum_{i=0}^{n}\binom{n}{i}(-\epsilon )^{i}
=1-n\epsilon +\frac{n(n-1)}{2}\epsilon ^{2}+...+\binom{n}{n}(-\epsilon )^{n}
=(1- \epsilon)^{n} \\
P_d &=\sum_{i=1}^{\left \lceil n/2 \right \rceil}\binom{n}{2i-1}\epsilon ^{2i-1}(1- \epsilon)^{n-2i+1}
=(1-\epsilon )^{n}\sum_{i=1}^{\left \lceil n/2 \right \rceil}\binom{n}{2i-1}(\frac{\epsilon }{1-\epsilon })^{2i-1}
=\frac{1-(1-2\epsilon )^{n}}{2} \\
P_{ud} &=\sum_{i=1}^{\left \lfloor n/2 \right \rfloor}\binom{n}{2i}\epsilon ^{2i}(1- \epsilon)^{n-2i}
=(1-\epsilon )^{n}\sum_{i=1}^{\left \lfloor n/2 \right \rfloor}\binom{n}{2i}(\frac{\epsilon }{1-\epsilon })^{2i}
=\frac{1+(1-2\epsilon )^{n}}{2}-(1-\epsilon )^{n} \\
1&\equiv P_0+P_d+P_{ud}
\end{aligned} \]
5. 单比特奇偶校验码性能与误比特概率的关系
从理论分析的角度,误比特率 ε 的取值范围为\( 0 \leqslant \epsilon \leqslant 1 \),首先分析 ε 的特殊取值情况,这些特殊取值的分析没有实际的工程应用价值,只对各概率计算公式的理解有一定帮助:
- ε = 0 时,表明无传输差错,\( P_0=1,P_d=P_{ud}=0 \)。此条件下,是不需要差错检测手段的;
- ε = 0.5 时,表明传输过程中,某个比特正确与否一半对一半,\( n \) 比特时有: \( P_0=(1/2)^n,P_d=1/2,P_{ud}=1/2-(1/2)^n \)。此条件下,发送方发0,接收方收到1的概率是50%,收到0的概率也是50%;当接收方收到1,发送方发0的概率是50%,发1的概率也是50%,这种情况的物理意义是接收方收到什么消息和发送方发送的消息毫无关系!为什么要聊这个呢?因为简中网对奇偶校验太不友好了,铺天盖地的说奇偶校验只有50%的检错率,而这个结论成立的前提是 ε = 0.5,有意义吗?若回头扯这个50%是说单比特奇偶校验只能检出一半数量的错误,只给人1个比特的(监督)校验位,谁又能检出超过一半数量的错误?
- ε = 1 时,表明传输过程中每个比特都是错的,\( P_0=0 \)。当 \( n \) 为奇数时,码字中错误比特数量为奇数,奇偶校验可检出此错误,故\( P_d=1,P_{ud}=0 \);当 \( n \) 为偶数时,码字中错误比特数量为偶数,奇偶校验不能检出此错误,故\( P_d=0,P_{ud}=1 \)。将 \( \epsilon=1 \) 代入\( P_0、P_d、P_{ud} \)各自的计算公式,可得到与分析一致的结果。此条件下,是不需要差错检测手段的,接收方只需将收到的每个比特取反即可获得正确的消息。
5.1 无差错概率P0与 ε 的一般关系
由无差错概率\( P_0 \)的计算公式\( P_{0}=(1-\epsilon )^n \),我们很容易知道:ε 从0单调递增至1时,\( P_0 \)将从1单调递减至0。更进一步地将\( P_0 \)对 ε 求导可得\( {P_0(\epsilon )}'=-n(1-\epsilon )^{n-1} \) ,在\( 0 \leqslant \epsilon \leqslant 1 \)区间内,\( {P_0(\epsilon )}'\leqslant 0 \),\( P_0 \)单调递减至0,同时 ε 越大,\( |{P_0(\epsilon )}'| \)越小,表明随着 ε 增大\( P_0 \)的下降速率减小。如下图所示:
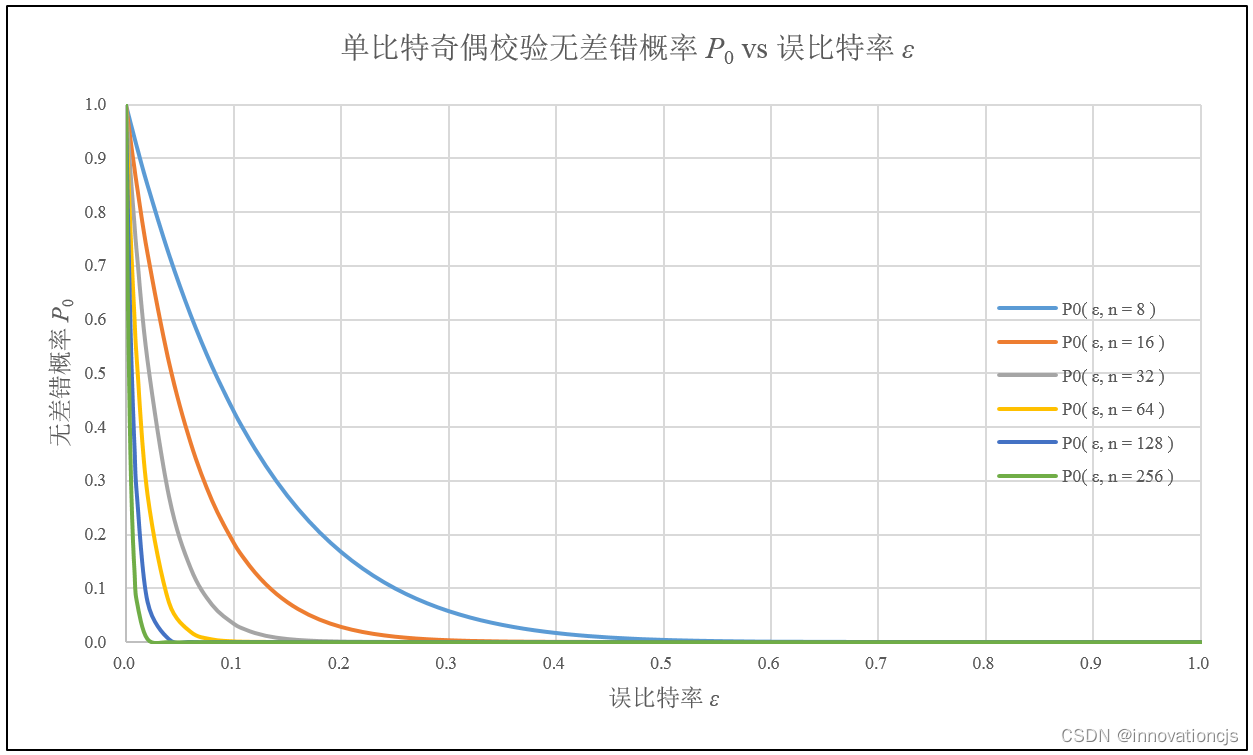
还是那句话,“可靠通信”首先是低误码率,单个码字的无差错概率低于90%的话,咋都不考虑了,故绘制\( P_0 \)与 ε 的局部关系,如下图所示(图中横轴为对数坐标):
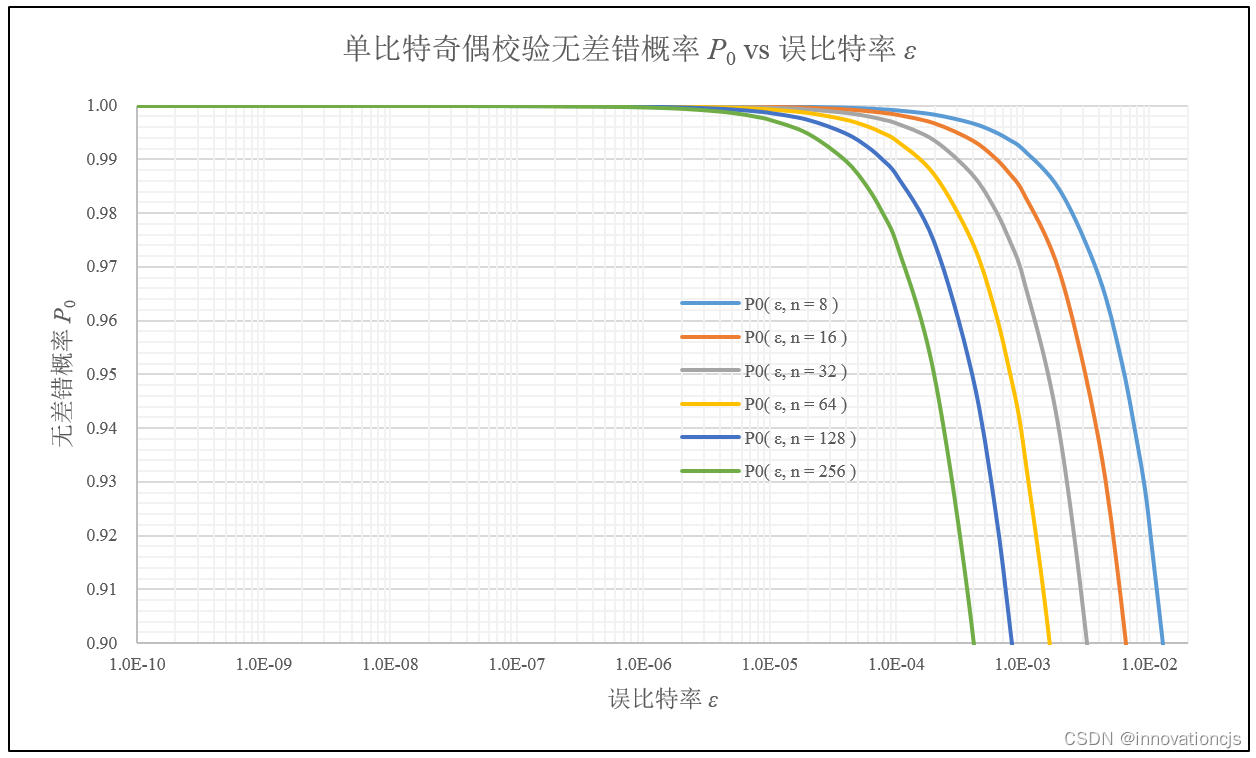
5.2 差错检出概率Pd与 ε 的一般关系
将差错检出概率计算公式\( P_d \)对 ε 求导可得\( {P_d(\epsilon )}'=n(1-2\epsilon )^{n-1} \),在\( 0 \leqslant \epsilon \leqslant 1 \)区间内,\( 1\geqslant (1-2\epsilon ) \geqslant -1 \),\( {P_d(\epsilon )}' \)的符号除了与 ε 的取值相关,还与 \( n \) 的奇偶性有关,当:
- \( n \) 为奇数时,在\( 0 \leqslant \epsilon \leqslant 1 \)区间内,\( {P_d(\epsilon )}'\geq 0 \),\( P_d \)单调递增(\( \lim_{\epsilon \rightarrow 1}P_d=1 \)),同时\( {P_d(\epsilon )}' \)是 ε 的凹函数,有\( {P_d(\epsilon=0.5 )}'=0 \),可知:在\( 0 \leqslant \epsilon \leqslant 0.5 \)区间内,\( P_d \)由0单调递增至0.5,且随着 ε 增大\( P_d \)的上升速率减小;在\( 0.5 \leqslant \epsilon \leqslant 1 \)区间内,\( P_d \)由0.5单调递增至1,且随着 ε 增大\( P_d \)的上升速率增大。
- \( n \) 为偶数时,在\( 0 \leqslant \epsilon \leqslant 0.5 \)区间内,\( {P_d(\epsilon )}'\geq 0 \),\( P_d \)单调递增(\( \lim_{\epsilon \rightarrow 0.5}P_d=0.5 \)),同时 ε 越大,\( {P_d(\epsilon )}' \)越小,\( P_d \)的上升速率减小;在\( 0.5 \leqslant \epsilon \leqslant 1 \)区间内,\( {P_d(\epsilon )}'\leq 0 \),\( P_d \)单调递减(\( \lim_{\epsilon \rightarrow 1}P_d=0 \)),同时 ε 越大,\( |{P_d(\epsilon )}'| \)越大,\( P_d \)的下降速率增大。
单比特奇偶校验差错检出概率与误比特率的一般关系如下图所示:
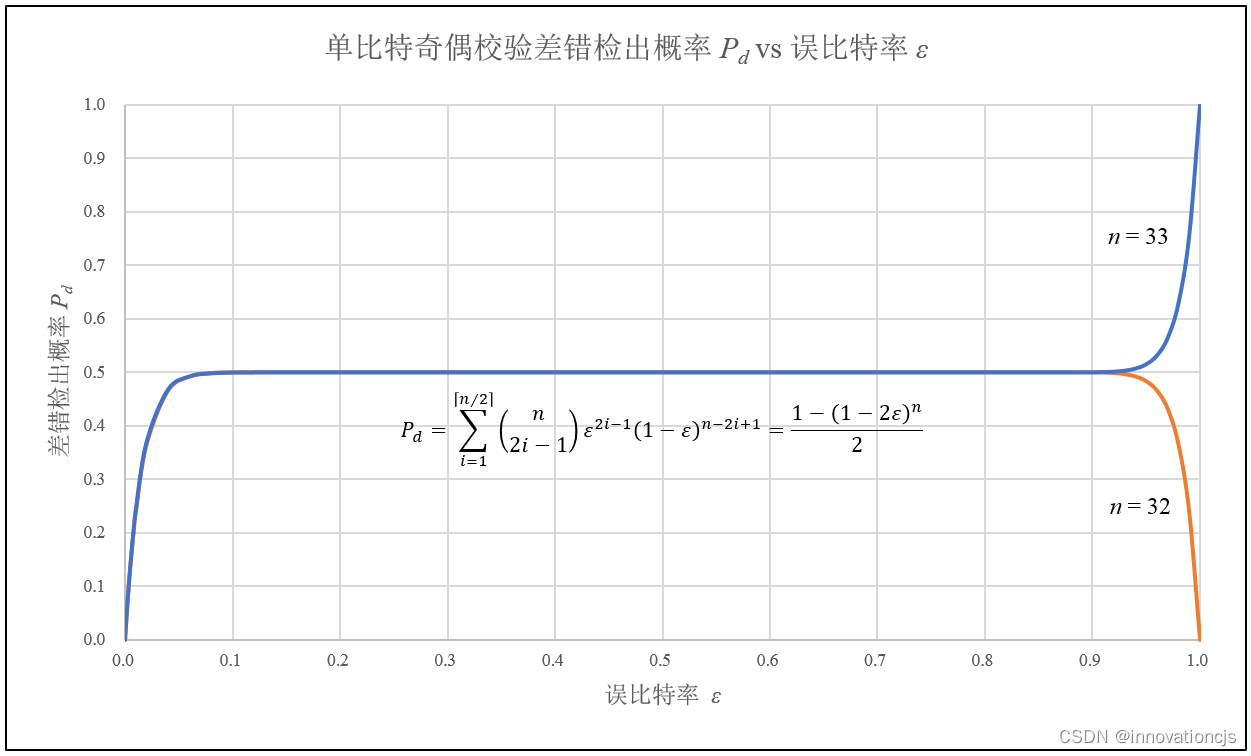
5.3 差错漏检概率Pud与 ε 的一般关系
将差错漏检概率计算公式\( P_{ud} \)对 ε 求导可得\( {P_{ud}(\epsilon )}'=n[(1-\epsilon )^{n-1}-(1-2\epsilon )^{n-1}] \),在\( 0 \leqslant \epsilon \leqslant 1 \)区间内,\( 1\geqslant (1-2\epsilon ) \geqslant -1 \),\( {P_{ud}(\epsilon )}' \)的符号除了与 ε 的取值相关,还与 \( n \) 的奇偶性有关。
当 \( n \) 为奇数时,在\( 0 \leqslant \epsilon \leqslant 2/3 \)区间内,\( {P_{ud}(\epsilon )}'\geq 0 \),但\( {P_{ud}(\epsilon )}' \)本身不是单调的,故\( P_{ud} \)在此区间单调递增,但随着 ε 增大,\( P_{ud} \)的上升速率先快后慢。在\( 2/3 \leqslant \epsilon \leqslant 1 \)区间内,\( {P_{ud}(\epsilon )}' \leq 0 \)且随着 ε 增大,\( |{P_{ud}(\epsilon )}'| \)增大,故\( P_{ud} \)在此区间单调下降至0,并随着 ε 增大,\( P_{ud} \)的下降速率增大。如下图所示:
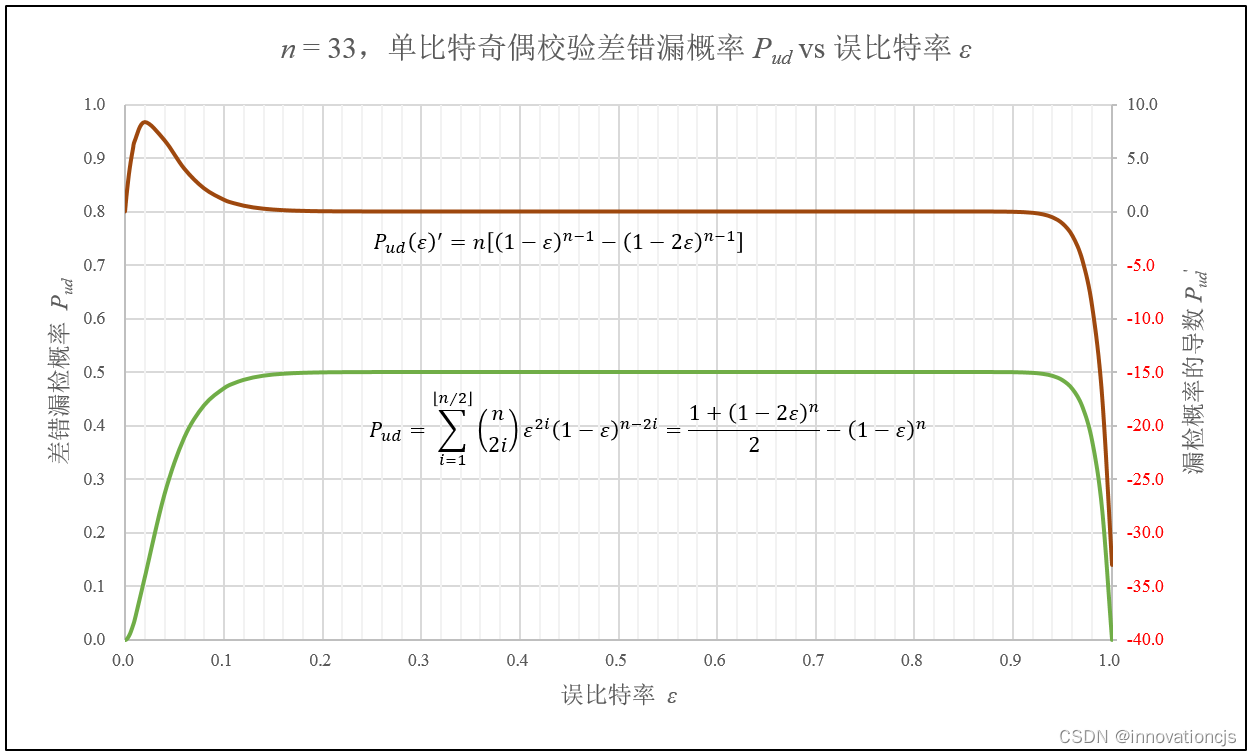
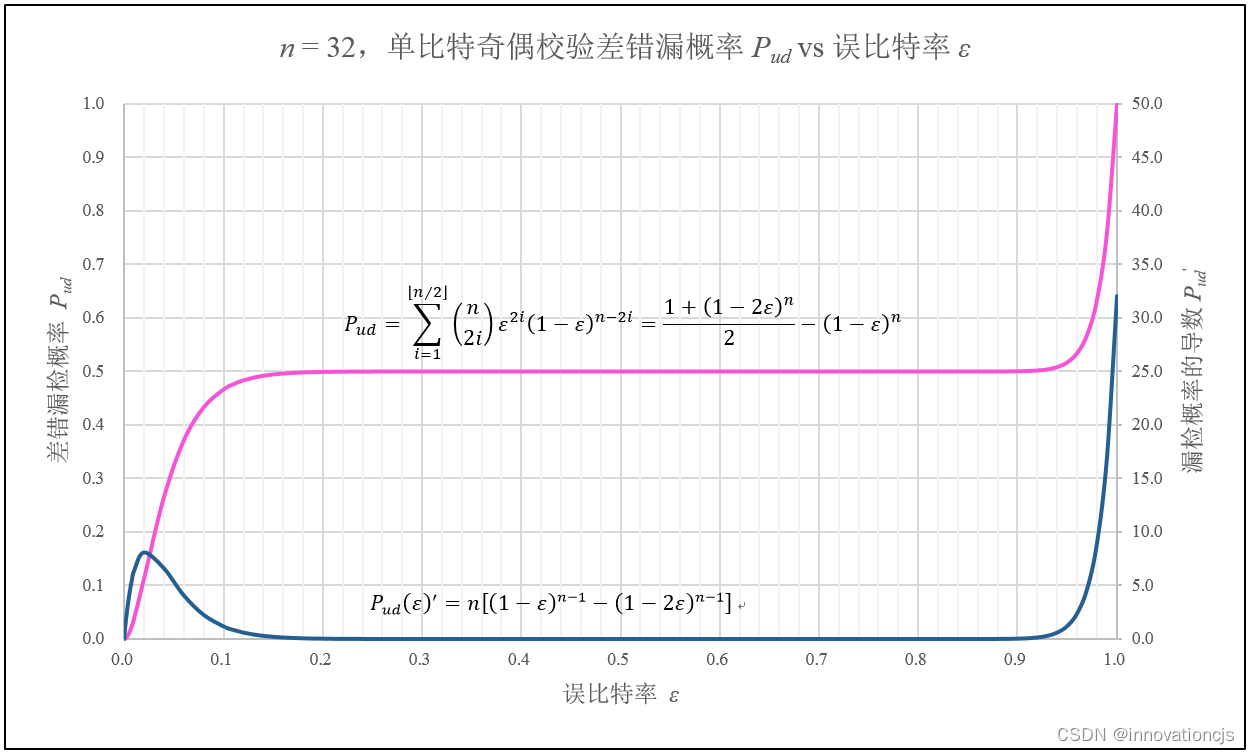
当 \( n \) 为偶数时,在\( 0 \leqslant \epsilon \leqslant 1 \)区间内,\( {P_{ud}(\epsilon )}'=n[(1-\epsilon )^{n-1}-(1-2\epsilon )^{n-1}] \geq 0 \),\( P_{ud} \)单调递增至1。应注意的是,在\( 0 \leqslant \epsilon \leqslant 2/3 \)区间内,\( {P_{ud}(\epsilon )}' \)不是单调的,意味着\( P_{ud} \)在此区间随 ε 的增大其上升速率先快后慢。如下图所示:
6. 单比特奇偶校验码性能与码字长度 n 的关系
整体而言,随着码字长度的增加,单比特奇偶校验的性能下降。
6.1 无差错概率P0与 n 的一般关系
由无差错概率的计算公式\( P_{0}=(1-\epsilon )^n \),我们很容易知道:随着码字长度的增加,无差错概率将单调下降至0。如下图所示:
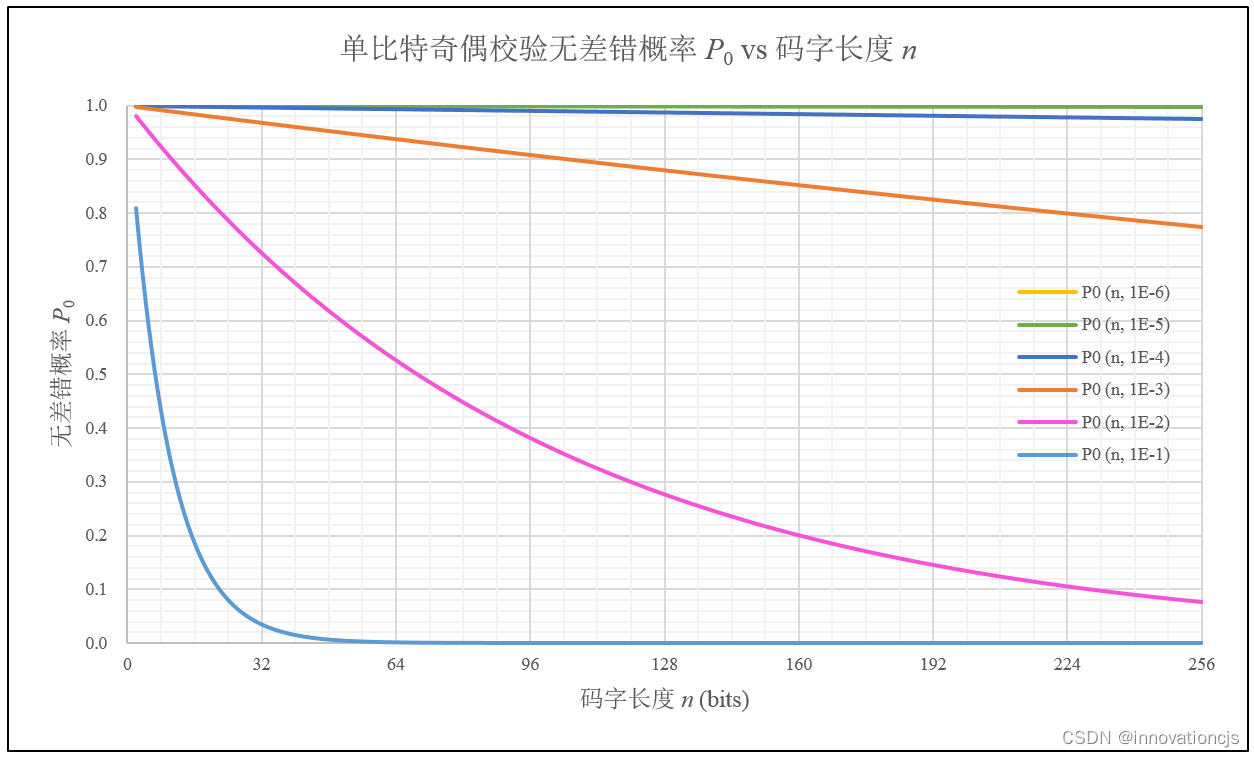
综合来看,单比特奇偶校验的无差错概率\( P_{0} \)将随着误比特率 ε、码字长度 \( n \) 的增加而减小(即性能下降),但应注意的是,对于二元对称信道下的数字通信系统,其无差错传输概率只与信道的误比特概率和码字长度相关,与采用的差错检测手段无关,定位于差错检测的编码技术(如奇偶校验、累加和校验、CRC校验)通常对应着低的信道误比特概率。
单独的差错检测编码,检测到错误时,只能选择丢弃或重传消息,对传输效率影响较大(即丢弃或重传的比特数通常远大于实际错误的比特数),当信道误比特概率难于降低(如无线信道),或传输速率很高时,人们通常会添加前向纠错编码(这超出了本文的讨论范畴),再结合检错编码,始终令检错编码保护的信息流有一个低的误比特概率。
6.2 差错检出概率Pd与 n 的一般关系
由差错检出概率的计算公式\( P_{d}=0.5-0.5(1-2\epsilon )^n \),我们很容易知道:在\( 0\leqslant \epsilon \leqslant 0.5 \) 区间内,随着码字长度的增加,差错检出概率将单调上升至0.5,ε 越大,随码字长度趋于0.5的速度越快。如下图所示(图中纵轴\( P_{d} \)为对数坐标):
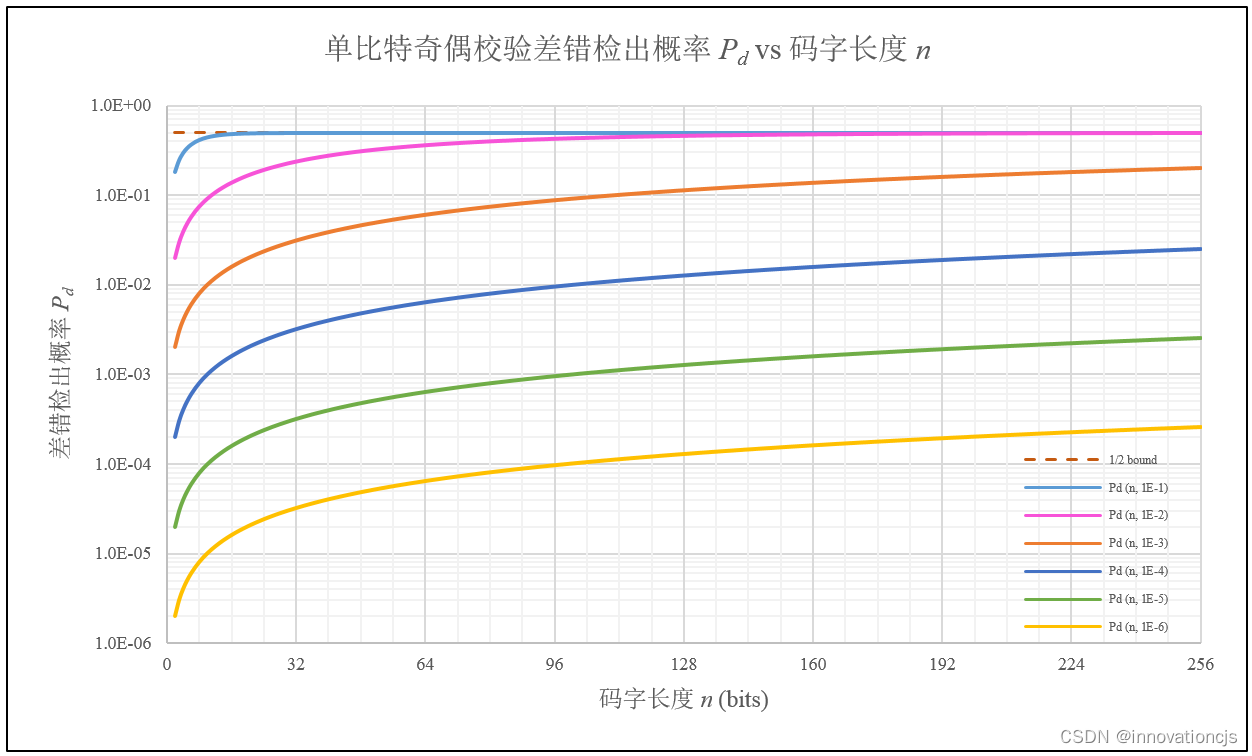
在\( 0.5 < \epsilon < 1 \)区间内,随着码字长度的增加,差错检出概率将随码字长度 \( n \) 的奇偶性振荡趋近于0.5,ε 越大,振荡幅度越大,随码字长度趋于0.5的速度越慢。如下图所示(图中横轴 \( n \) 为对数坐标):
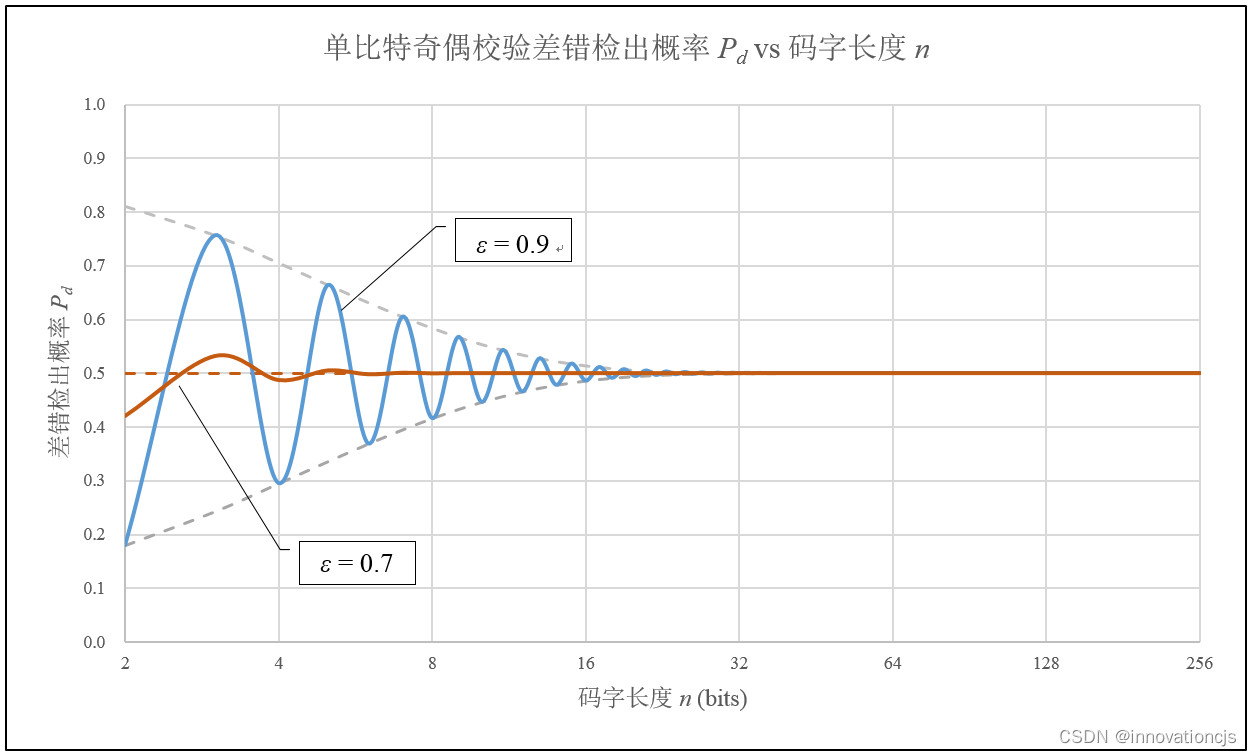
6.3 差错漏检概率Pud与 n 的一般关系
由差错漏检概率的计算公式\( P_{ud}=0.5+0.5(1-2\epsilon )^n-(1-\epsilon )^n \),我们很容易知道:在\( 0\leqslant \epsilon \leqslant 0.5 \)区间内,随着码字长度的增加,差错漏检概率将单调上升至0.5,ε 越大,随码字长度趋于0.5的速度越快。如下图所示(图中纵轴\( P_{ud} \)为对数坐标):
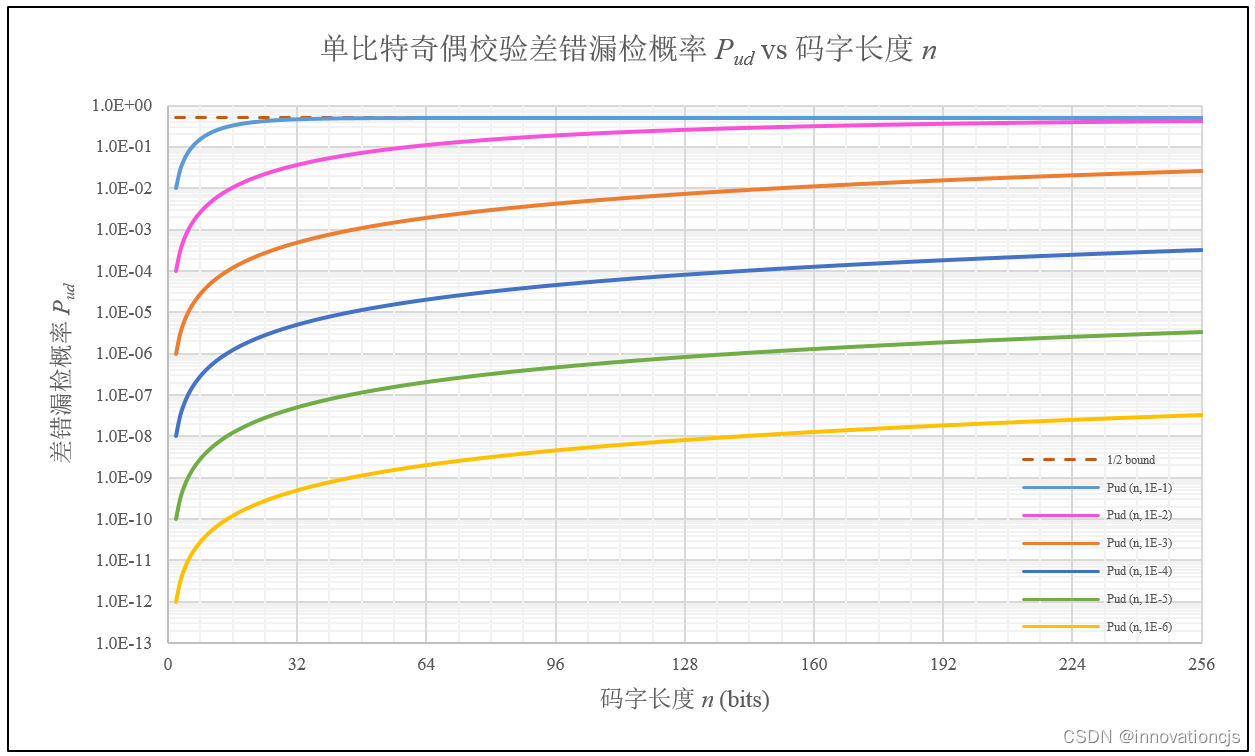
在\( 0.5 < \epsilon < 1 \)区间内,随着码字长度的增加,差错漏检概率将随码字长度 \( n \) 的奇偶性振荡趋近于0.5,ε 越大,振荡幅度越大,随码字长度趋于0.5的速度越慢。如下图所示(图中横轴 \( n \) 为对数坐标):
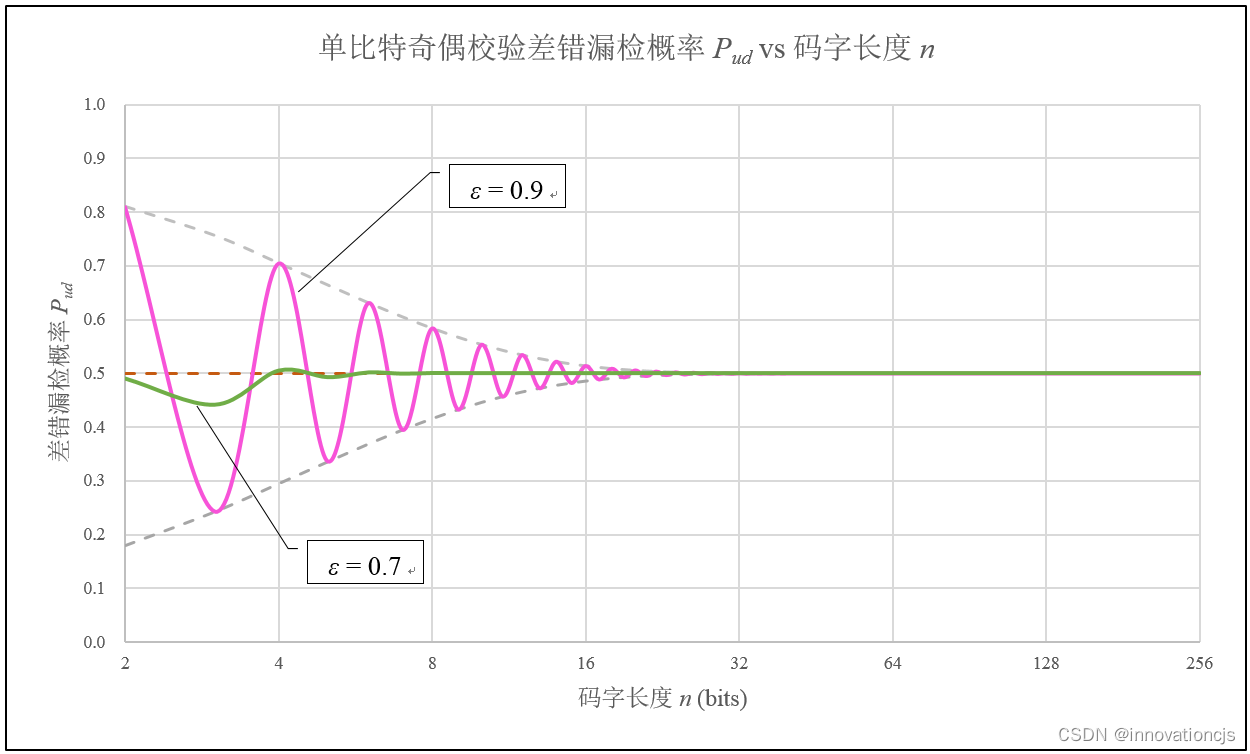
7. 单比特奇偶校验码实例
在对单比特奇偶校验的差错漏检概率深入研究后,笔者对工作中接触到的几个通讯总线的单码字奇偶校验性能进行了评估。它们都是单比特奇偶校验,各自的码字长度、校验规则和性能评估汇总如下:
- UART:含校验位的单个码字长度6 ~ 9 bits,奇校验或偶校验。9-bits码字长度,误比特率不提太高要求,按\( \epsilon =10^{-6} \)预算,UART单码字的差错漏检概率大致为\( 3.6\times 10^{-11} \);
- MIL-STD-1553B:含校验位的单个码字长度17-bits,奇校验。其规范明确规定了在AWGN信道下的字差错率\( < 10^{-7} \),折算的误比特率大约为\( 5\times 10^{-9} \),此条件下,1553B总线单码字的差错漏检概率大致为\( 3.4\times 10^{-15} \);
- ARINC-429:含校验位的单个码字长度32-bits,奇校验。其规范未明确规定在AWGN信道下的误比特率,但给出了电磁兼容试验条件下的误比特率要求:\( < 10^{-7} \),按此预算,ARINC-429单码字的差错漏检概率大致为\( 4.96\times 10^{-12} \);
- PCI:含校验位的单个码字长度37-bits,偶校验。其规范未对总线的误比特率作出明确规定,但作为有着良好电气规范约束的板级总线,\( \epsilon =10^{-9} \)是很低的要求了(依笔者的使用经验,可以低至\( 10^{-12} \)),按\( \epsilon =10^{-9} \)预算,PCI总线单码字的差错漏检概率大致为\( 6.66\times 10^{-16} \)。
为不失一般性,特绘制上述4个总线的单码字奇偶校验性能曲线,如下图所示(图中纵轴、横轴均为对数坐标):
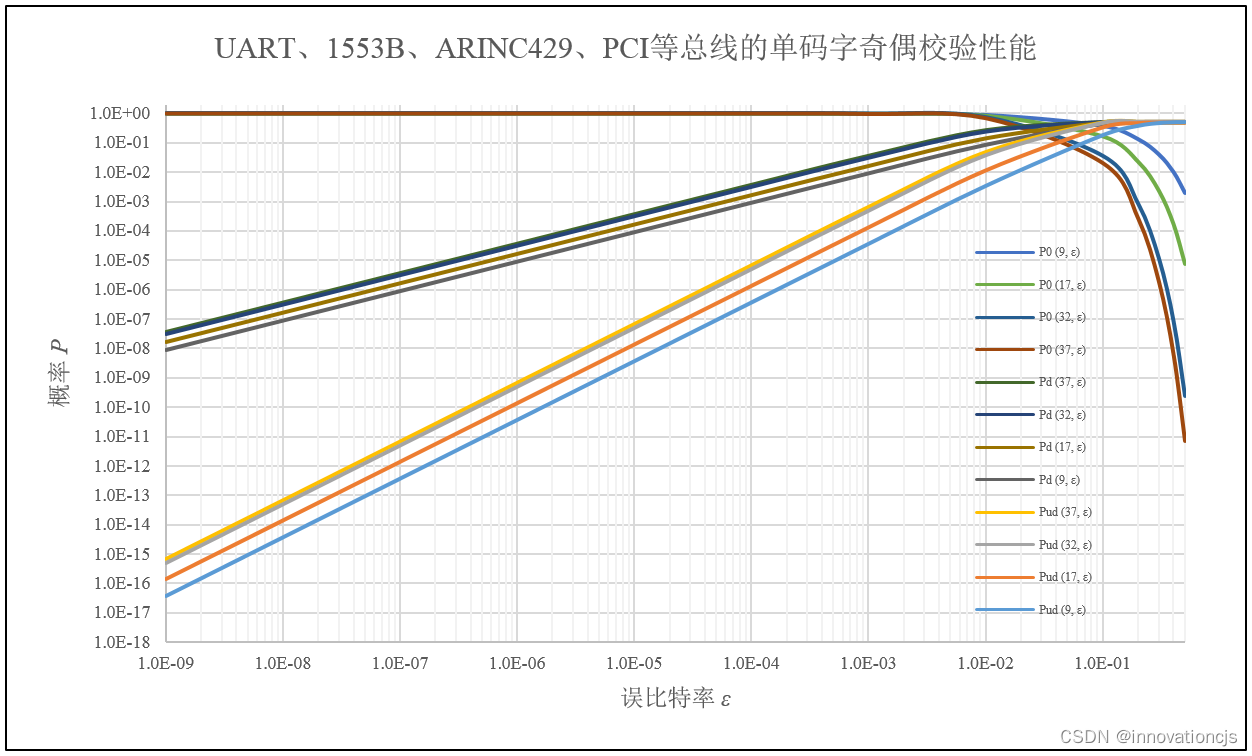





















 3809
3809











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








