Ants (KM算法)

Young naturalist Bill studies ants in school. His ants feed on plant-louses that live on apple trees. Each ant colony needs its own apple tree to feed itself.

Bill has a map with coordinates of n ant colonies and n apple trees. He knows that ants travel from their colony to their feeding places and back using chemically tagged routes. The routes cannot intersect each other or ants will get confused and get to the wrong colony or tree, thus spurring a war between colonies.

Bill would like to connect each ant colony to a single apple tree so that all n routes are non-intersecting straight lines. In this problem such connection is always possible. Your task is to write a program that finds such connection.

On this picture ant colonies are denoted by empty circles and apple trees are denoted by filled circles. One possible connection is denoted by lines.

Input

The first line of the input file contains a single integer number n (1 ≤ n ≤ 100) — the number of ant colonies and apple trees. It is followed by n lines describing n ant colonies, followed by n lines describing n apple trees. Each ant colony and apple tree is described by a pair of integer coordinates x and y (− 10 000 ≤ x, y ≤ 10 000 ) on a Cartesian plane. All ant colonies and apple trees occupy distinct points on a plane. No three points are on the same line.

Output

Write to the output file n lines with one integer number on each line. The number written on i-th line denotes the number (from 1 to n) of the apple tree that is connected to the i-th ant colony.

Sample Input

5
-42 58
44 86
7 28
99 34
-13 -59
-47 -44
86 74
68 -75
-68 60
99 -60

Sample Output

4
2
1
5
3

题目大意：

在坐标系中有N只蚂蚁，N棵苹果树，给你蚂蚁和苹果树的坐标。让每只蚂蚁去一棵苹果树，

一棵苹果树对应一只蚂蚁。这样就有N条直线路线，问：怎样分配，才能使总路程和最小，且

N条线不相交。

思路：

用一个图来说明思路。

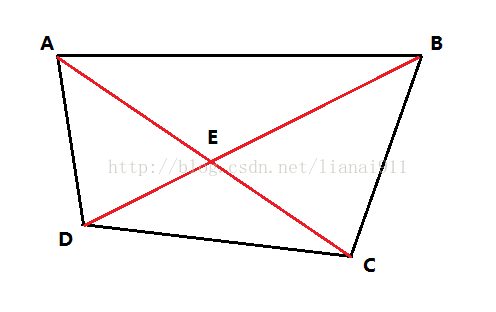
假设A、B为蚂蚁，C、D为苹果树。则存在两种匹配：第一种是AD、BC，第二种是AC、BD。

根据三角形不等式AD+BC < AC+BD，最后得到很重要的一个性质——满足总路程之和最小

的方案一定不相交。现在来构建二分图，一边为蚂蚁，另一边为苹果树，以距离为边权值，题

目就变为了求带权二分图最小权和的最佳匹配。反向来思考，将距离乘以-1取负值建图，那么

就变为了求带权二分图最大权和的最佳匹配。直接用KM算法来做。

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<math.h>
#define Inf 0x3fffffff
using namespace std;
const double eps = 1e-6; 
const int N = 150;
struct node{
	double x,y;
}p1[N],p2[N];
double dx[N],dy[N];
double slack[N];
double e[N][N];
int vx[N],vy[N];
int match[N];
int n;
double Dis(node a,node b){
	double X=(a.x-b.x)*(a.x-b.x);
	double Y=(a.y-b.y)*(a.y-b.y);
	return -sqrt(X+Y);
}
int Find(int u){
	vx[u]=1;
	for(int i=1;i<=n;i++){
		if(vy[i]) continue;
		double gap=dx[u]+dy[i]-e[u][i];
		if(fabs(gap)<=eps){
			vy[i]=1;
			if(match[i]==-1||Find(match[i])){
				match[i]=u;
				return 1;
			}
		}
		else slack[i]=min(gap,slack[i]);
	}
	return 0;
}
void KM(){
	memset(dy,0,sizeof(dy));
	memset(match,-1,sizeof(match));
	for(int i=1;i<=n;i++){
		dx[i]=-Inf;
		for(int j=1;j<=n;j++)
	     dx[i]=max(dx[i],e[i][j]);
	}
	
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++)
		   slack[j]=Inf;
		while(1){
			memset(vx,0,sizeof(vx));
			memset(vy,0,sizeof(vy));
			if(Find(i)) break;
			double dis=Inf;
			for(int j=1;j<=n;j++)
			   if(!vy[j]) dis=min(dis,slack[j]);
			for(int j=1;j<=n;j++){
				if(vx[j]) dx[j]-=dis;
				if(vy[j]) dy[j]+=dis;
				else slack[j]-=dis;
			}
		}
	}
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	   scanf("%lf%lf",&p1[i].x,&p1[i].y);
    for(int i=1;i<=n;i++)
       scanf("%lf%lf",&p2[i].x,&p2[i].y);
    for(int i=1;i<=n;i++) 
    for(int j=1;j<=n;j++)
    e[i][j]=Dis(p1[i],p2[j]);
    KM();
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
       if(match[j]==i){
       	 printf("%d\n",j);
       	 break;
	   }
	return 0;
}