SLAM中的非线性优化和BA总结

一、非线性最小二乘问题

  先考虑简单的问题：$$\underset{x}{\min }\frac{1}{2}||f(x)|{|}_2^2$$1.当$f$很简单时：令$\frac{df}{dx}=0$,将得到极值点或鞍点，比较这些解即可。
2.当$f$复杂时（$f$为n元函数）：$\frac{df}{dx}$难求，或$\frac{df}{dx}=0$很难解，此时使用迭代方式来求解。

  迭代的方式为：

1. 给定某个初始值$x_0$。
2. 对于第k次迭代，寻找一个增量$\Delta x_k$，使得$||f(x_k+\Delta x_k)|{|}_2^2$达到极小值。
3. 若$\Delta x_k$足够小，则停止。
4. 否则，令$x_{k+1}=x_k+\Delta x_k$，返回2。

  这里需要确定增量的方法（即梯度下降策略）：一阶的或二阶的。首先需要对其进行泰勒展开得到：$$||f(x_k+\Delta x_k)|{|}_2^2\approx ||f(x)|{|}_2^2+J(x)\Delta x+\frac{1}{2}\Delta x^{T}H\Delta x$$  若只保留一阶梯度：$\underset{\Delta x}{\min }||f(x)|{|}_2^2+J\Delta x$，增量的方向为：$\Delta x^{\ast }=-J^T(x)$.（通常还需要计算步长），该方法称为最速下降法。
  若保留二阶梯度：$\Delta x^{\ast }=arg\min ||f(x)|{|}_2^2+J(x)\Delta x+\frac{1}{2}\Delta x^{T}H\Delta x$，则得到（令上式关于$\Delta x$的导数为零）：$$H\Delta x=-J^T$$该方法称为牛顿法。

  最速下降法和牛顿法虽然直观，但使用当中存在一些缺点：

1. 最速下降法由于过于贪婪可能导致迭代次数的增多
2. 牛顿法迭代次数少，但需要计算复杂的Hessian矩阵

  因此，可以通过Gauss-Newton和Levenberg-Marquadt来回避Hessian的计算。

二、理解Gauss-Newton，Levenburg-Marquadt等下降策略

Gauss-Newton

一阶近似$f(x)$：$f(x+\Delta x)\approx f(x)+J(x)\Delta x$
平方误差变为：$$\frac{1}{2}||f(x)+J(x)\Delta x|{|}^2=\frac{1}{2}(f(x)+J(x)\Delta x{)}^T(f(x)+J(x)\Delta x)=\frac{1}{2}(||f(x)|{|}_2^2+2f(x{)}^{T}J(x)\Delta x+\Delta x^{T}J(x{)}^{T}J(x)\Delta x)$$令关于$\Delta x$导数为零：$2J(x{)}^{T}f(x)+2J(x{)}^{T}J(x)\Delta x=0$$$J(x{)}^{T}J(x)\Delta x=-J(x{)}^{T}f(x)$$
记为：$$H\Delta x=g$$
  G-N用J的表达式近似了H。
步骤如下：

1. 给定初始值$x_0$。
2. 对于第k次迭代，求出当前的雅可比矩阵$J(x_k)$和误差$f(x_k)$。
3. 求解增量方程：$H\Delta x_k=g$。
4. 若$\Delta x_k$足够小，则停止。否则，令$x_{k+1}=x_k+\Delta x_k$。

Levenberg-Marquadt

  Gauss-Newton简单实用，但$\Delta x_k=H^{-1}g$当中无法保证H可逆（二次近似不可靠）。
  而Levenberg-Marquadt方法一定程度上改善了它。
  G-N属于线搜索方法：先找到方向，再确定长度；L-M属于信赖区域方法，认为近似只在区域内可靠。
  在L-M中考虑近似程度的描述$\rho =\frac{f(x+\Delta x)-f(x)}{J(x)\Delta x}$即实际下降/近似下降。若太小，则减小近似范围；若太大，则增加近似范围。

  LM的流程如下：

1. 给定初始值$x_0$，以及初始优化半径$\mu$。
2. 对于第k次迭代，求解：$$\underset{\Delta x_k}{\min }\frac{1}{2}||f(x_k)+J(x_k)\Delta x_k|{|}^2,s.t.||D\Delta x_k|{|}^2\le \mu$$其中$\mu$是信赖域的半径。
3. 计算$\rho$。
4. 若$\rho >\frac{3}{4}$，则$\mu =2\mu$;
5. 若$\rho <\frac{1}{4}$，则$\mu =0.5\mu$;
6. 如果$\rho$大于某个阈值，认为近似可行。令$x_{k+1}=x_k+\Delta x_k$。
7. 判断算法是否收敛。如不收敛则返回2，否则结束。

  在信赖域内的优化，利用拉格朗日乘子转化为无约束：$$\underset{\Delta x_k}{\min }\frac{1}{2}||f(x_k)+J(x_k)\Delta x_k|{|}^2+\frac{\lambda }{2}||D\Delta x|{|}^2$$仍参照高斯牛顿法展开，增量方程为：$$(H+\lambda D^{T}D)\Delta x=g$$在Levenberg方法中，取D=I，则：$$(H+\lambda I)\Delta x=g$$  LM相比于GN，能够保证增量方程的正定性，即认为近似只在一定范围内成立，如果近似不好则缩小范围；从增量方程上来看，可以看成一阶和二阶的混合，参数$\lambda$控制着两边的权重，如果$\lambda$为0，则为$H\Delta x=g$，即采用二阶方法牛顿法；如果$\lambda$非常的大，则采用一阶方法最速下降法。

三、BA

  首先，误差是什么？如何表示。BA中待优化的变量是位姿和路标点，如何求误差函数关于位姿和路标点的导数？李代数扰动模型是什么？雅可比矩阵式什么？在BA中具体由怎样的形式？
  旋转矩阵群与变换矩阵群：$$SO(3)=R\in {\mathbb{R}}^{3\times 3}|R{R}^T=I,det(R)=1$$$$SE(3)=\left\{T=\left[\begin{array}{cc}R& T\\ 0^T& 1\end{array}\right]\in {\mathbb{R}}^{4\times 4}|R\in SO(3),t\in {\mathbb{R}}^3\right\}$$具有连续光滑性质的群叫做李群，存在问题：对加法不封闭，无法求导。

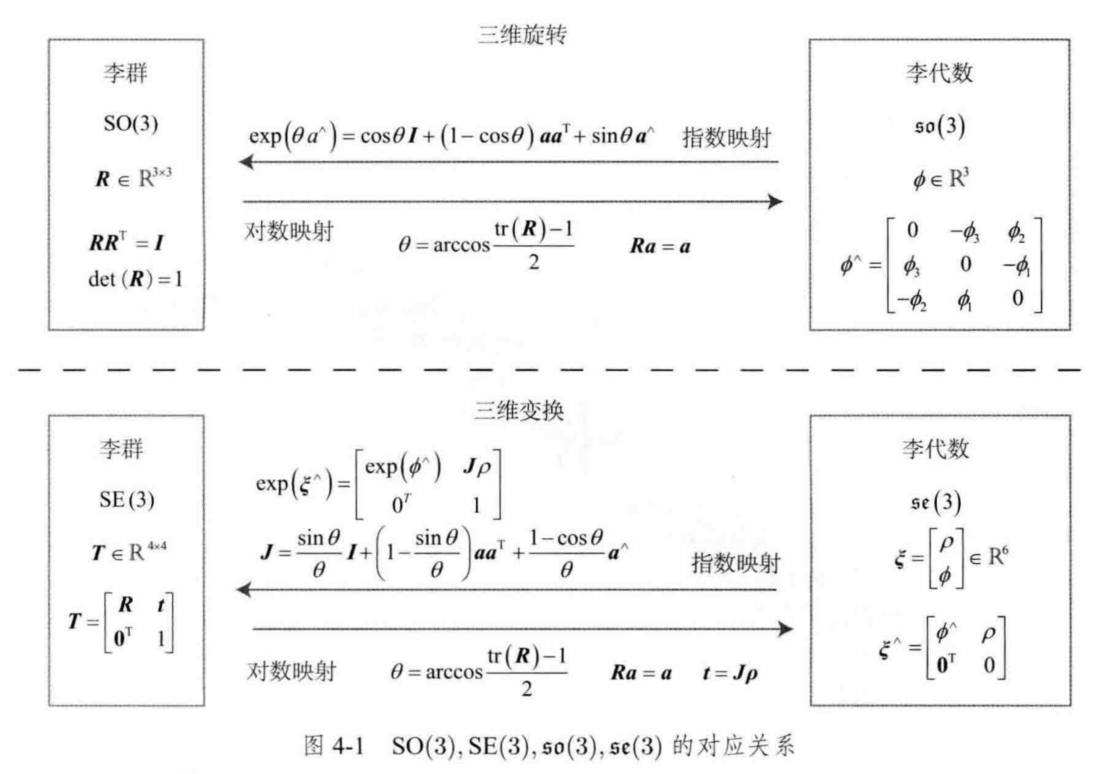
  求导的方式有两种：

1. 对R对应的李代数加上小量，求相对于小量的变化率（导数模型）；
2. 对R左乘或右乘一个小量，求相对于小量的李代数的变化率（扰动模型）：
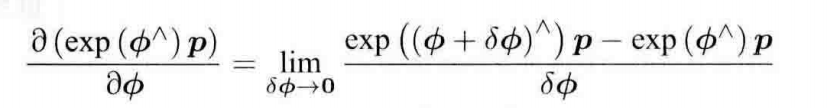
   在扰动模型（左乘）中，左乘小量，令其李代数为零，得：
   
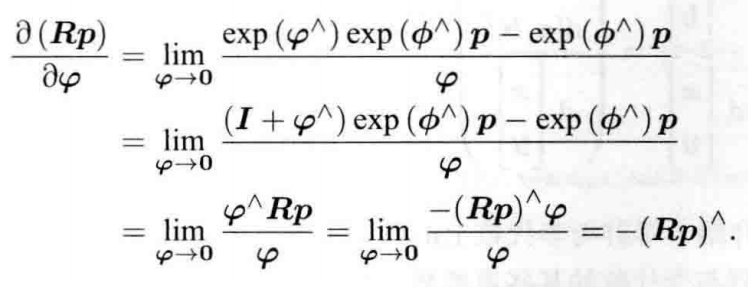
   而位姿变换的导数模型为：
   

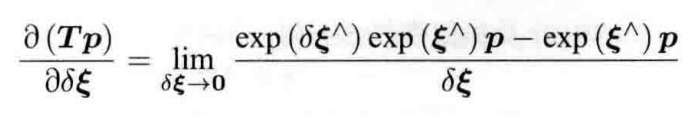
四、图优化与g2o

重投影误差：

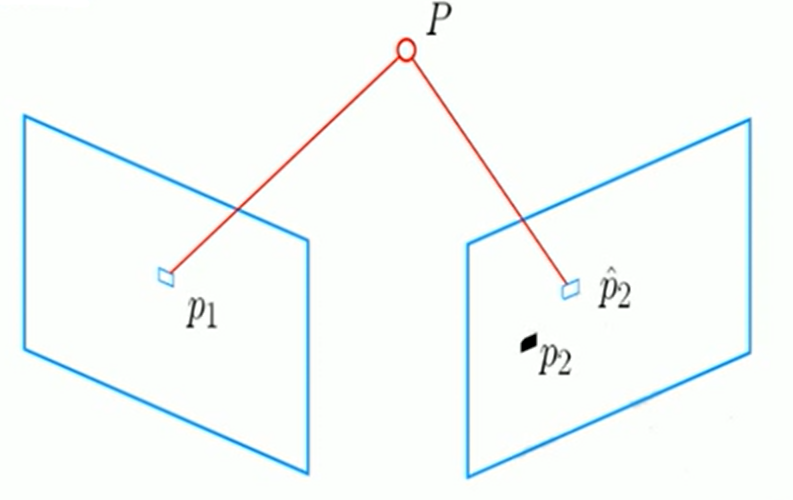
构建关于误差函数的最小二乘问题：

矩阵形式：$$s_i{u}_i=Kexp({\xi }^{\wedge })P_i$$误差函数：$${\xi }^{\ast }=arg\underset{\xi }{\min }\frac{1}{2}\sum _{i=1}^n||u_i-\frac{1}{s_i}Kexp({\xi }^{\wedge })P_i|{|}_2^2$$把该误差函数记为$e(x)$：$$e(x+\Delta x)=e(x)+J(x)\Delta x$$相机模型：$$u=f_x\frac{X^{\prime }}{Z^{\prime }}+c_x,v=f_y\frac{Y^{\prime }}{Z^{\prime }}+c_y$$利用扰动模型求导：




我们将求得的两项导数相乘得：

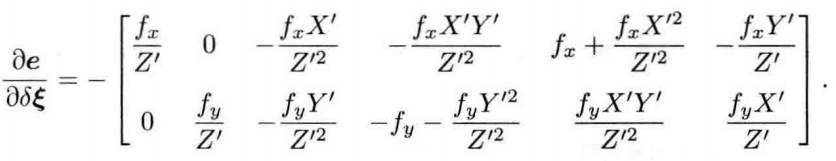
该矩阵即为我们所求得雅可比矩阵，在优化中指导着迭代的方向，使相机的位姿得到优化。

优化特征的空间点位置：

该矩阵为优化特征点空间位置时的雅可比矩阵，指导着迭代的方向。